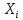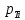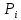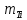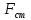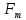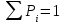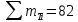МатМод в ГР. МатМод в ГР 2022. Имеются данные об интервалах поступления автомобилей на базу строительных материалов. Интервалы поступления автомобилей даны в минутах. Требуется определить закон распределения случайной величины
 Скачать 252.42 Kb. Скачать 252.42 Kb.
|
|
Задание. Имеются данные об интервалах поступления автомобилей на базу строительных материалов. Интервалы поступления автомобилей даны в минутах. Требуется определить закон распределения случайной величины.
Решение. Полученный ряд значений случайной величины называется простым статистическим рядом. Обработка статистического ряда выполняется в следующем порядке: 1 Все данные располагаются в порядке возрастания или убывания значения случайной величины. Например, исходные данные можно расположить в порядке возрастания. Полученный ряд называется вариационным. Он уже дает некоторое представление об изучаемой случайной величине. Составим вариационный ряд:
Данные вариационного ряда разбиваются на группы или классы. Эта операция, называемая табулированием или группировкой, выполняется для того, чтобы представить распределение в более компактной и наглядной форме. Величину интервала групп предлагается определять по следующей формуле: 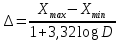 где Xmax и Xmin – соответственно максимальное и минимальное значения в вариационном ряду; D – количество значений в вариационном ряду. В данном случае: Xmax=94, Xmin=2, D=90. 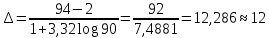 Выбранные значения интервалов групп в порядке возрастания выписываются в таблицу 1. Некоторые значения могут значительно отличаются от остальных в вариационном ряду, в этом случае они признаются ложными и вычеркиваются из рассмотрения. Границы интервалов групп показываются черточками на вариационном ряду. Если значение находится на границе i-го и (i+1)-го интервалов, то значение учитывается в (i+1)-ом интервале. Необходимо отметить, что число групп (n) зависит от объема выборки, но для определения типа распределения случайной величины принимается обычно 10-12. Однако возможно принимать величину интервала групп условно, в зависимости от плотности распределения. По вариационному ряду подсчитывается число наблюдений в каждой группе mi. Далее необходимо рассчитать среднее значение случайной величины в группе: 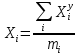 где 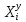 – y-ый элемент i-ой группы; – y-ый элемент i-ой группы; mi – количество наблюдений в группе i. Частота значений случайной величины в каждой группе определяется по формуле: 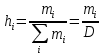 Результаты показателей статистического распределения сводим в таблицу 1. Таблица 1 — Расчет показателей статистического распределения
Среднее в группе, Хi: 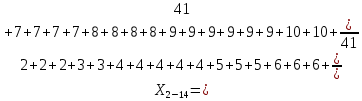 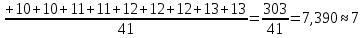 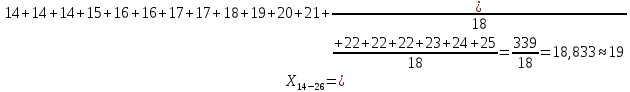 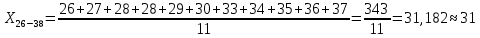 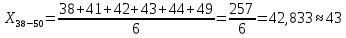 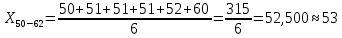 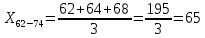 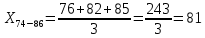 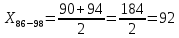 Частота появления события, hi: 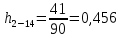 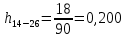 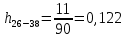 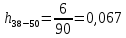 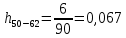 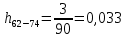 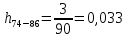 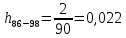 Xi×hi: X2-14×h2-14=7×0,456=3,367 X14-26×h14-26=19×0,200=3,767 X26-38×h26-38=31×0,122=3,811 X38-50×h38-50=43×0,067=2,856 X50-62×h50-62=53×0,067=3,500 X62-74×h62-74=65×0,033=2,167 X74-86×h74-86=81×0,033=2,700 X86-98×h86-98=92×0,022=2,044 (Xi – Xср)2×hi: (X2-14– Xср)2×h2-14=(7–24,211)2×0,456=128,896 (X14-26– Xср)2×h14-26=(19–24,211)2×0,200=5,784 (X26-38– Xср)2×h26-38=(31–24,211)2×0,122=5,939 (X38-50– Xср)2×h38-50=(43–24,211)2×0,067=23,119 (X50-62– Xср)2×h50-62=(53–24,211)2×0,067=53,351 (X62-74– Xср)2×h62-74=(65–24,211)2×0,033=55,458 (X74-86– Xср)2×h74-86=(81–24,211)2×0,033=107,499 (X86-98– Xср)2×h86-98=(92–24,211)2×0,022=102,119 Числовые характеристики, определяемые по выборке, являются приближенными оценками соответствующих характеристик генеральной совокупности. Оценки любого параметра должны быть: состоятельными, т.е. при увеличении числа объектов D сходиться по вероятности к соответствующим параметрам генеральной совокупности, несмещенными, т.е. чтобы при оценке параметра по выборке не делалось систематической ошибки в сторону увеличения или уменьшения параметра, и эффективными, т.е. чтобы они имели наименьшую дисперсию. Всем этим требованиям удовлетворяет выборочное среднее, определяемое по формуле: 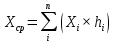 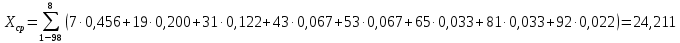 Выборочная дисперсия определяется по формуле: 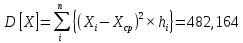 Надежность и точность оценок определяется доверительным интервалом для выборочного среднего: 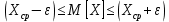 где ε – величина отклонения, которая определяется по следующей формуле: 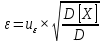 где uε – величина, определяемая для принятого уровня значимости P∆ при числе наблюдений ≥ 20 по таблицам функции Лапласа, в нашем случае при P∆=0,05, uε=1,96, тогда: 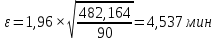 Таким образом, доверительные границы равны: 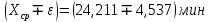 Интенсивность потока определяется по следующей формуле: 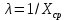 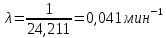 Вероятность появления в одной точке: 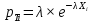 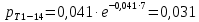 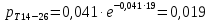 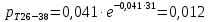 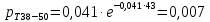 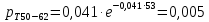 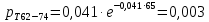 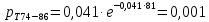 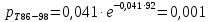 Вероятность появления в группе: 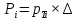 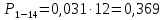 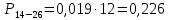 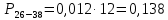 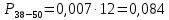 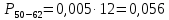 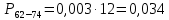 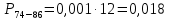 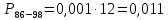 Число значений случайной величины в соответствующей группе по теоретическому распределению: 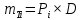 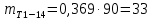 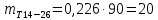 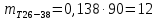 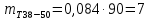 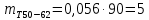 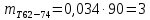 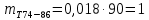 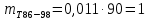 Согласование практического и теоретического распределения оцениваем по критерию Колмогорова. Для чего необходимо выполнить нижеприведенные вычисления. Значения статистической функции распределения: 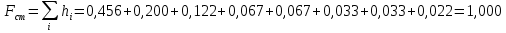 Значения теоретической функции распределения: 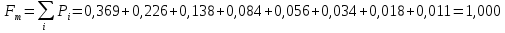 Для каждой группы определяется абсолютное значение разности и выбирается наибольшее Rm: 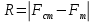 Расчеты по подбору теоретической кривой представлены в таблице 2. Таблица 2 – Подбор теоретической кривой
Значение критерия Колмогорова определяется по следующей формуле: 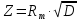 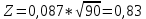 По значению Z определяется вероятность Pz(таблица 3) того, что полученные отклонения вызваны случайными колебаниями величины выборки. Таблица 3 – Зависимости Pzот Zдля критерия Колмогорова
Если Pz[0,864;1], то можно говорить о хорошем согласовании теоретического распределения с выборочным, если Pz [0,544;0,864) об удовлетворительном. В нашем случае Pz=0,544, что говорит об удовлетворительном согласовании теоретического распределения с выборочным. Для наглядности эмпирическое распределение изображается в виде гистограммы, а теоретическое в виде кривой (рисунок 1).            Хi Pi, hi 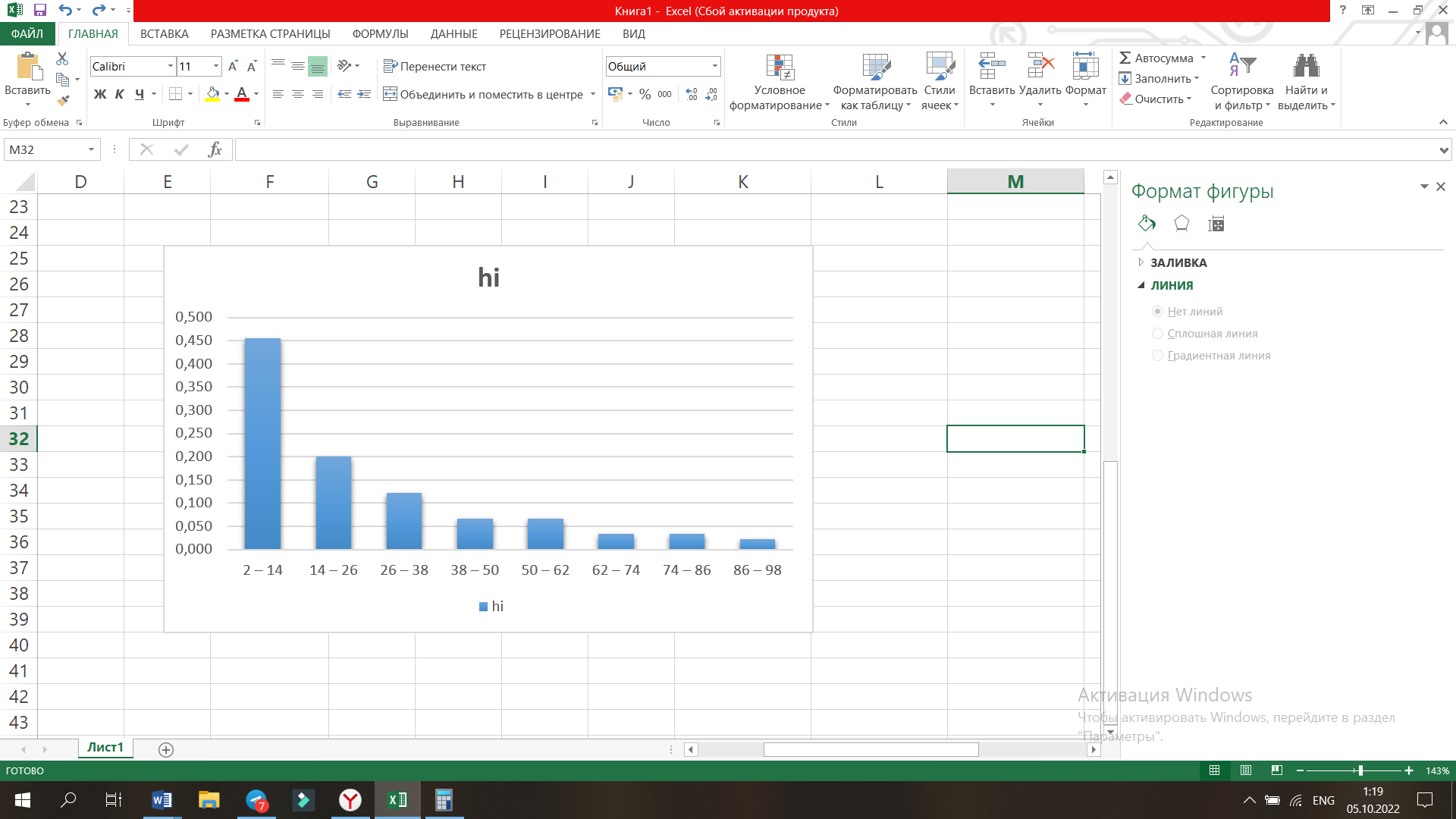 Рисунок 1 – Эмпирическое и теоретическое распределение случайной величины |