Имеются следующие данные за год по заводам одной по заводам одной промышленной компании
 Скачать 52.37 Kb. Скачать 52.37 Kb.
|
Практическое задание
дисциплине
Пермь 2022 Задача 1. Имеются следующие данные за год по заводам одной по заводам одной промышленной компании.
На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три. РЕШЕНИЕ ЗАДАЧИ 1. Определим выработку: Величину интервала рассчитаем по формуле: 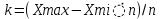 , где хmax, xmin – максимальное и минимальное значения объема продукции, а n – количество групп. , где хmax, xmin – максимальное и минимальное значения объема продукции, а n – количество групп.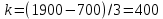 Определим границы 3-х групп: 700-1100 1100-1500 1500-1900 Рассчитаем показатели по каждой группе. Сначало вычислим выработку на одного рабочего количество произведенной продукции по формуле: 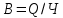 , где В-выработка продукции, количество произведенной продукции в натуральных или стоимостных показателях, Ч-численность работников. , где В-выработка продукции, количество произведенной продукции в натуральных или стоимостных показателях, Ч-численность работников. Группа 1 700-1100
Итого: 6 5230 2430 3380 0.646 Группа 2 1100-1500
Итого: 4 5390 3900 6150 1.141 Группа 3 1500-1900
12550_1.467_Результаты_групп_в_таблице'>Итого: 5 8550 8850 12550 1.467 Результаты групп в таблице
Выводы: с увеличением количества рабочих увеличиваются основные фонды и выработка продукции на одного человека. 3адача 2. Выпуск продукции на заводе в 2020 г. составил 160 млн руб. По плану на 2021 г. предусматривалось выпустить продукции на 168 млн руб., фактически же выпуск составил 171,36 млн руб. Вычислите относительные величины планового задания и выполнения плана. РЕШЕНИЕ ЗАДАЧИ 2 Вычислим относительные показатели по формулам: ОВПЗ (относительная величина планового задания) 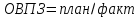 *100%= *100%=168: 160 *100%=105% ОВВП (относительная величина выполнения плана) 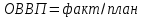 * 100% = * 100% = 171.36:168*100%=102% ВЫВОД: на 2021 год планировалось увеличить выпуск продукции по сравнению 2020 года на 5%, фактически план выпуска продукции был перевыполнен на 2%. Задача 3. На основании данных, представленных в таблице, определите установленную среднюю продолжительность трудового дня производственного рабочего по заводу в целом:
РЕШЕНИЕ ЗАДАЧИ В первую очередь надо узнать сколько людей работает по цехам и заводу в целом. 1цех-3*600=1800 2 цех-3*800=2400 3 цех-2*400=800 4 цех-1*200=200 Итого на заводе работают 5200 человек, из них 5000 человек работают по 8 часов, что составляет 96.2% людей. По 6 часов работает 200 человек, что составляет 3.2% людей. Теперь узнаем среднюю продолжительность смены: 8*96.2%=6*3.2%=7,888 ВЫВОД: средняя продолжительность смены по заводу составляет 7,888 часов. Задача 4. Имеются следующие данные о распределении рабочих цеха по размеру месячной заработной платы:
Определите среднюю месячную зарплату рабочих цеха, моду и медиану, среднеквадратическое отклонение икоэффициент вариации. РЕШЕНИЕ ЗАДАЧИ Определим среднюю месячную зарплату по формуле 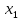 =2.5+5/2=3.75 =2.5+5/2=3.75 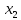 =5+7,5/2=6,25 х3=7,5+10/2=8,75 =5+7,5/2=6,25 х3=7,5+10/2=8,75 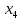 =10+12,5/2=11,25 х5=12,5+15/2=13,75 =10+12,5/2=11,25 х5=12,5+15/2=13,75х=3,75*15+6,25*15+8,75*25+11,25*65+13,75*30/150=1512,5/150=10,083 Средняя заработная плата составляет 10,083 тыс.руб. Этот ряд имеет равные интервалы, то мода находится в интервале наибольшей частотой, то есть в интервале 10,0 - 12,5 тыс. руб. Следовательно, её можно вычислить по формуле: Mb=xₙ+h* 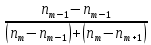 Нижняя граница модального интервала, величина модального интервала: 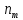 -частота модального периода, -частота модального периода,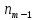 предмодального периода, предмодального периода, 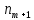 постмодального периода постмодального периодаMb= 10,0+2,5* 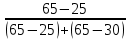 =11,33 =11,33Медиана определяется по формуле Ме= xₙ+h 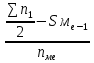 , нижняя граница медианного периода, величина медианного периода, , нижняя граница медианного периода, величина медианного периода,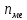 -частость медианного периода, -частость медианного периода,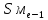 -накопленная частость предмедианного периода -накопленная частость предмедианного периодаМе= 10,0+2.5 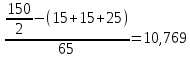 Ответ:медиана ровна 10,769 Ответ:медиана ровна 10,769 Дисперсию можно определить по формуле: 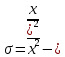 x=10,083 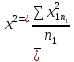 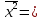 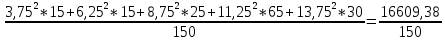 =110,729 =110,729 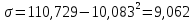 Среднеквадратическое отклонение: 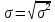 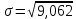 =3,021 =3,021Коэффициент вариации:V= 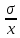 *100% V= *100% V=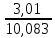 *100%=29,852% *100%=29,852%Выборка однороднна т.к V=29,852%<33% Задача 5. Объем продукции на промышленном предприятии повысился в 2016 году по сравнению с 2011 годом на 100 млн рублей в сопоставимых ценах, или на 25 %. В 2021 году объем продукции увеличился по сравнению с 2016 годом на 20 %. Определите: 1) объем выпуска продукции предприятия в 2011, 2016, 2021 годах; 2) среднегодовые темпы прироста выпуска продукции за: а) 2011-2021 гг.; б) 2016-2021 гг.; в) 2011-2016 гг. РЕШЕНИЕ ЗАДАЧИ: Вычислим объем выпуска продукции на промышленном предприятии 2011 г-вп=100/0,25=400 млн.руб 2016 г-вп=400+100=500 млн.руб 2021 г-вп=500*(1+0,2)=600 млн.руб. Темпы прироста выпуска продукции 1)С 2011 по 2021 гг =103,8% 2)С 2016 по 2021 гг = 103,1% 3)С 2011 по 2016 гг =103,75% Ответ: С 2011 по 2016 гг объем выпуска продукции на предприятии увеличивался на 3,8%, с 2016 по 2021 гг темп прироста продукции за каждый год состовлял 3,1%, а за весь период с 2011 по 2021 гг объем выпуска продукции предприятия увеличивался на 3,75%. Задача 6. По одному из предприятий промышленности стройматериалов имеются следующие данные:
Определите общий индекс цен и сумму роста или снижения объема реализации продукции за счет изменения цен. Определения общего иендекса : Ig= 100 – 2 = 98% = 0.98 Ig = 100+5 = 105% = 1.05 I = p1g1|ig*p0g0 1960+2100+440/0.98*1960 +1.05*2100+1*440 = 4500/1920.8+2205+440 = 0.986 = 98.6% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
