Главная страница
Навигация по странице:

  • Порядок выполнения задания, методические указания

  • Задание №2. Сколькими способами читатель может выбрать две книжки из шести имеющихся

  • Задание №4. Дан неориентированный граф. Определить ‒ диаметр и радиус этого графа; ‒ центры графа

  • Задание №5. Определить, сколькими способами можно попасть из пункта х в пункт у и найти кратчайший маршрут из х в у.

    		•

    Дискретная_19_ИВТз-201_Тарасов_2. Индивидуальная расчетная работа 2 Вариант 19 Комбинаторика и теория графов. Цель работы


    Скачать 84.17 Kb.
    НазваниеИндивидуальная расчетная работа 2 Вариант 19 Комбинаторика и теория графов. Цель работы
    Дата27.03.2022
    Размер84.17 Kb.
    Формат файлаdocx
    Имя файлаДискретная_19_ИВТз-201_Тарасов_2.docx
    ТипМетодические указания
    #420755

    Индивидуальная расчетная работа №2

    Вариант №19

    Комбинаторика и теория графов.

    Цель работы: закрепить навыки определения количества выборок с использованием основных формул комбинаторики, навыки вычисления числовых характеристик графов.

    Порядок выполнения задания, методические указания:

    - ознакомиться с теоретическими положениями по данной теме;

    - изучить схему решения задач;

    - выполнить задания индивидуальной расчетной работы.

    Выполнил: студент группы ИВТз-201 Тарасов И. И.

    Задание №1. Перед нами 10 закрытых замков и 10 похожих ключей к ним. К каждому замку подходит только один ключ, но ключи смешались. Возьмем один из замков, назовем его первым и попробуем открыть его каждым из 10 ключей. В лучшем случае он откроется первым же ключом, а в худшем - только десятым. Сколько нужно в худшем случае произвести проб, чтобы открыть все замки?

    X=10+9+8+7+6+5+4+3+2+1=55

    Задание №2. Сколькими способами читатель может выбрать две книжки из шести имеющихся?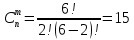



    Задание №3. Задать граф, представленный множеством вершин и ребер, графически и матрицами, вычислить степени его вершин.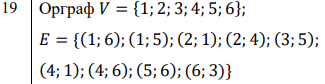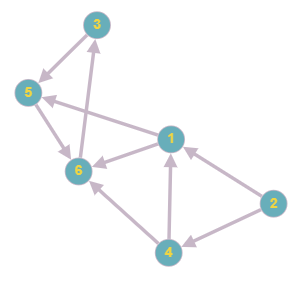





    Матрица смежности:

    0
    0
    0
    0
    1
    1

    1
    0
    0
    1
    0
    0

    0
    0
    0
    0
    1
    0

    1
    0
    0
    0
    0
    1

    0
    0
    0
    0
    0
    1

    0
    0
    1
    0
    0
    0

    Матрица инцидентности:

    1
    1
    -1
    0
    0
    -1
    0
    0
    0

    0
    0
    1
    1
    0
    0
    0
    0
    0

    0
    0
    0
    0
    1
    0
    0
    0
    -1

    0
    0
    0
    -1
    0
    1
    1
    0
    0

    -1
    0
    0
    0
    -1
    0
    0
    1
    0

    0
    -1
    0
    0
    0
    0
    -1
    -1
    1

    Степени вершин:

    𝑝(1) = 2, 𝑝(2) = 2, 𝑝(3) = 1, 𝑝(4) = 2, 𝑝(5) = 1, 𝑝(6) = 1

    Задание №4. Дан неориентированный граф. Определить ‒ диаметр и радиус этого графа; ‒ центры графа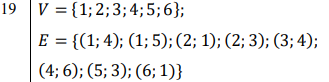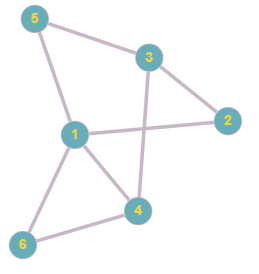





    Матрица минимальных расстояний графа:

    0
    1
    2
    1
    1
    1

    1
    0
    1
    2
    2
    2

    2
    1
    0
    1
    1
    2

    1
    2
    1
    0
    2
    1

    1
    2
    1
    2
    0
    2

    1
    2
    2
    1
    2
    0

    Радиус графа: 2. Диаметр графа: 2. Центры: все вершины.

    Задание №5. Определить, сколькими способами можно попасть из пункта х в пункт у и найти кратчайший маршрут из х в у.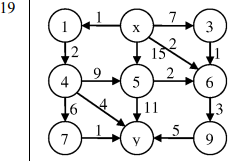



    Количество путей из 2(x) в 8(y) равно 8.

    Кратчайший маршрут: 2(х)⇒1⇒4⇒8(у), расстояние между вершинами 7.

    написать администратору сайта