5 практика. 5 практика моя). Индивидуальные задания I
 Скачать 33.99 Kb.
|
|
Индивидуальные задания I Имеются 2 системы, в одной из которых резервирование выполнено для отдельных систем (левый рисунок), в другой – резервирование выполнено для отдельных элементов (правый рисунок). В системах отдельные элементы функционируют при экспоненциальном законе плотности распределения вероятности отказов. Принять каждого элемента =0,510-4 1/ч 1. Необходимо определить, какая схема более надёжна. 2. Построить графики зависимости вероятности безотказной работы от времени для каждой системы. 3. Сделать вывод о зависимости вероятности безотказной работы от чисел M=9 и N=14. 4   . Определить, какое минимальное число элементов должно входить в схему с резервированием систем, чтобы её надёжность (вероятность безотказной работы) была эквивалентна надёжности (вероятности безотказной работы) схемы с резервированием элементов. Будет ли результат решения задачи зависеть от времени (от текущей наработки изделия)?Решение: Система, в которой резервирование выполнено для отдельных систем (левый рисунок), представляет собой общее резервирование с постоянно включенным резервом и целой кратностью. Вероятность безотказной работы в данном случае определяется по формуле: 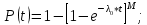 а среднее время безотказной работы по формуле: 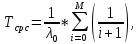 где 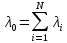 – интенсивность отказов нерезервированной системы или любой из 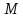 резервных систем.Вычисляем: 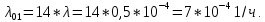 Тогда: 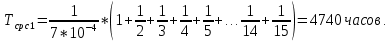 Система, в которой резервирование выполнено для отдельных элементов (правый рисунок), представляет собой раздельное резервирование с постоянно включенным резервом и целой кратностью. Вероятность безотказной работы в данном случае определяется по формуле: 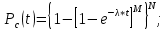 а среднее время безотказной работы по формуле: 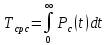 Тогда воспользовавшись Exele построим зависимость вероятности безотказной работы от времени и определим Tcp. 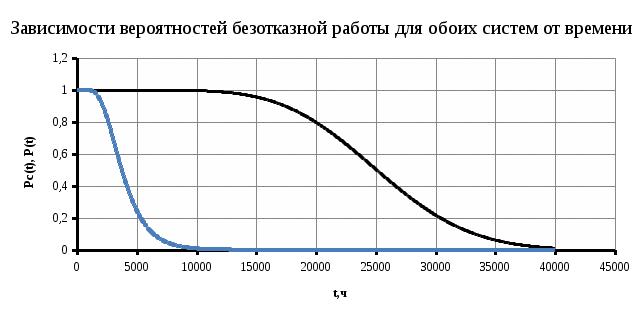   P(t) Pc(t) Вывод: исходя из решения данной задачи и графика, приведенного выше, можно сделать вывод о том, что система, в которой резервирование выполнено для отдельных систем (левый рисунок) менее надежна, чем система, где резервирование выполнено для отдельных элементов (правый рисунок). Так же можно сделать вывод о зависимости вероятности безотказной работы от чисел M и N. Так при увеличении числа М вероятность безотказной работы системы будет увеличиваться, а при увеличении числа N вероятность безотказной работы системы будет уменьшаться. Задача 3 В системе телеконтроля могут быть применены схемы резервирования с дробной кратностью каналов “два из трех” или “три из пяти”. Интенсивность отказов одного канала =5,010-4 1/ч. Требуется определить, какая схема имеет большую вероятность безотказной работы в течение наработки до отказа. Для каждой схемы резервирования построить зависимости Pс(t) и с(t). Закон распределения плотности вероятности отказов – экспоненциальный. 1. Система со схемой резервирования с дробной кратностью “два из трех” В этом случае система “два из трех” работоспособна, если работоспособны не менее 2-х элементов из 3-х. При экспоненциальном законе распределения функция надежности будет иметь вид: 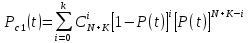 P(t) = e-λt -надежность 1 элемента; К=1 - число отказавших элементов; i - номер 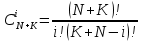комбинации;  - число комбинации, которое возможно при данном значении комбинации;N = 2 - число элементов, необходимых для нормальной работы Тогда: 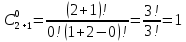 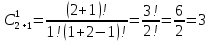 Тогда воспользовавшись Mathcad построим график зависимости безотказной работы от времени. |