Индивидуальный образовательный маршрут учащегося по теме Умножение и деление натуральных чисел. Индивидуальный образовательный маршрут (умн-е и дел-е нат чисел). Индивидуальный образовательный маршрут к теме умножение и деление натуральных чисел Умения

• Название: Индивидуальный образовательный маршрут к теме умножение и деление натуральных чисел Умения
• Анкор: Индивидуальный образовательный маршрут учащегося по теме Умножение и деление натуральных чисел
• Дата: 29.12.2022
• Размер: 121.23 Kb.
• Имя файла: Индивидуальный образовательный маршрут (умн-е и дел-е нат чисел).rtf
• Тип: Документы; #868586

Индивидуальный образовательный маршрут к теме умножение и деление натуральных чисел

1. Умения: Умножать и делить нацело натуральные числа, находить значение числового выражения.

Система задач.

1. Вычислите.

а) 35 · 100 = в) 352 · 261 = д) 12700 : 100 =


б) 172 · 11 = г) 39 : 3 = е) 2730 : 78 =


2. Найдите значения выражений.

а) (78 + 34) · (21 – 19) =
б) (280 + 162) : (223 – 2) =

3. Найдите значения выражений.

а) (29 · 16) – (11 · 3) =
б) 784 + (255 : 5) =
в) 72 · (32 – (42 : 21)) =
2. Умения: Записывать и использовать буквенную запись переместительного и сочетательного свойств умножения для нахождения значения числового и буквенного выражения.

Система задач.

1. Найдите значения выражений.

а) 37 · 11 · 15 =
б) (24 · 6) · 5 =
в) (31 · 4) · (5 · 18) =
г) 25 · 125 · 4 · 8 =
2. Найдите значения выражений.

а) (123 · а) · b, если а = 400, b = 25.


б) (35 · а) : 7, если а = 49.


в) (2 · а · b) : (с · d), если а = 8, b = 26, с = 13, d = 4.


3. Умения: Уметь распознавать уравнение, содержащее в записи знаки «·» и «:», и находить его корень.

Система задач.

1. Решите уравнения.

а) х · 81 = 243 в) 526 : х = 263

б) 11 · у = 99 г) у : 35 = 81

2. Решите уравнения.

а) 30х + 12х = 252 в) 180 : (3х + 6х) = 10

б) (12х – 3х) : 18 = 10 г) 10х + 2х + 62 = 302

4. Умение: Делить натуральные числа с остатком. Система задач.

1. Найдите остаток от деления.

а) 73 на 14; б) 1928 на 17; в) 476 на 17.
2. Найдите неполное частное от деления.

а) 383 на 11; б) 672 на 345; в) 1073 на 37.
3. Найдите делимое, если делитель 34, неполное частное 3, а остаток 29.
4. Назовите наименьшее трёхзначное число, которое при делении на 21 даёт в остатке 11.
5. Умения: Записывать и использовать буквенную запись распределительного свойства умножения для нахождения значения числового и буквенного выражения.

Система задач.

1. Вычислите.

а) (2 + 17) · 3 =

б) 3 · 11 – 2 · 11 =

в) (12 – 4) · 5 =

г) 15 · 7 – 15 · 4 =

2. Запишите выражения в виде суммы.

а) (а + 14) · 5 = в) (а + 2) · 5 – 12 =

б) (7 – b) · 2 = г) 13 + (11 – а) · 4 =

3. Найдите значения выражений.

а) 3 · 11 + 7 · 11 + 19 · 11 =
б) 2 · 14 + 35 · 14 – 17 · 14 =
в) a × x + b × x + x × c , если а = 3, b = 4, с = 5, х = 6.

6. Умения: Определить порядок действий и упрощать выражения на основе свойств всех действий с натуральными числами.

Система задач.

1. Найдите значения выражений.

а) 3 · 7 · 20 : 6 =

б) 256 : 4 · 13 =

в) 721 + 168 – 351 + 12 =

г) 35 · 27 – 96 : 12 =

2. Упростите выражения.

а) 7а + 13а – 11а =

б) (25х + 14х) – (19х + 6х) =

в) 19z – (13z – 6z) =

3. Найдите значения выражений.

а) (72 + 12 · 4) – (35 : 7 – 1) =

б) 35 + (72 : 9 + (35 – 2 · 6)) =

в) 126 : 9 + 3 · 17 – 2 · (12 – 7) =

г) (3х – 2у) · (3х + 2у), если х = 28, у = 11


7. Умение: Находить квадрат и куб натурального числа.

Система задач.

1. Вычислите.

а) 3² = б) 4³ = в) 7² =

г) 42³ = д) (3 + 12)² = е) (421 – 295)³ =

2. Вычислите.

а) (32 : 8 + 3)² =

б) (2² + 3³)² =

в) ((7 + 3)²)³ =

г) (9³ – 7²)³ =

3. Найдите значения выражений.

а) (3а)², если а = 19.

б) ((7а + b)³)², если а = 0, b = 5.

в) 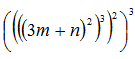, если т = 0, п = 1.


8. Умение: Использовать формулы для нахождения площади прямоугольника и объёма параллелепипеда.

Система задач.

1. Дан прямоугольник со сторонами а и b. Найдите его площадь. Задание выполнить в таблице.

а	b	s
17	2
14	83
15	15
10351	1

2. Площадь прямоугольника равна 256 дм². Найдите его длину, если ширина равна 8 дм.

3. Вычислите объём прямоугольного параллелепипеда с измерениями, равными 3 см, 10 см и 15 см.

4. Длина прямоугольника больше его ширины на 13 см. Найдите площадь прямоугольника, если его периметр равен 46.

5. Найдите высоту прямоугольного параллелепипеда, если известно, что площадь его основания равна 72 см², а объём – 504 см³.

9. Умение: Находить значение числового и буквенного выражения, содержащего различные действия, а также степени.

Система задач.

Найдите значения выражений:

а) 37 · 2³ – 35 : 7 + (11² + 7³) =


б) (22 + 7)² · (53 – 7²)³ · 18 =


в) (а + b)² + (2а – 8b)³ · 17 – (25 : b)², если а = 21, b = 5.


г) (3 · х + 12 · х – 7 · х)³ · (14 – х)² + (32 : у)³, если х = 10, у = 16.


10. Умения: Моделировать условие текстовой задачи и решать аналитическим способом (с помощью уравнения, содержащего в записи знаки «·», «:»).

Система задач.

1. Масса двух мешков с картофелем 84 кг, причём первый мешок в 3 раза тяжелее второго. Найдите массу первого мешка.
2. В смеси сухофруктов содержатся 5 частей сушёных яблок и 3 части кураги. Сколько граммов сушёных яблок надо взять для приготовления 640 г такой смеси?

3. Геологи ехали до лагеря 4 ч на грузовике и 3 ч на автобусе. Всего проехали 233 км. С какой скоростью ехал автобус, если скорость грузовика была 32 км/ч?