Инерциальные и неинерциальные системы отсчёта.. Инерциальные и неинерциальные системы отсчёта. Инерция
 Скачать 50.07 Kb.
|
|
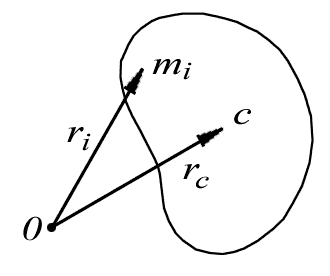
Инерциальные и неинерциальные системы отсчёта. Инерция – это явление, при котором тело стремится сохранить свое первоначальное состояние. Если оно двигалось, то оно должно стремиться к тому, чтобы сохранять скорость этого движения. А если оно покоилось, то будет стремиться сохранить свое состояние покоя. Инертность – это свойство тела сохранять состояние движения. Свойство инертности характеризуется такой величиной, как масса. Чем тело тяжелее, тем его труднее сдвинуть с места или, наоборот, остановить. Инерциальные системы отсчёта имеют непосредственное отношение к понятию «инерциальная система отсчета» (ИСО), о которой речь будет ниже. Чтобы понять эти ситемы, рассмотрим движение тела (или состояние покоя) в случае, если на тело не действуют другие тела. Заключение о том, как будет вести себя тело в отсутствии действия других тел, впервые было предложено Рене Декартом: если тело движется и на него не действуют другие тела, то движение будет сохраняться, оно будет оставаться прямолинейным и равномерным. Если же на тело не действуют другие тела, а тело покоится, то будет сохраняться состояния покоя. Но известно, что состояние покоя связано с системой отсчета, в одной СО тело покоится, а в другой вполне успешно и ускоренно движется. Результаты опытов и рассуждений приводят к выводу о том, что не во всех системах отсчета тело будет двигаться прямолинейно и равномерно или находиться в состоянии покоя при отсутствии действия на него других тел. Следовательно, для решения главной задачи механики важно выбрать такую систему отчета, где все-таки выполняется закон инерции, где ясна причина, вызвавшая изменение движения тела. Если тело будет двигаться прямолинейно и равномерно в отсутствии действия других тел, такая система отсчета будет для нас предпочтительной, а называться она будет инерциальной системой отсчета (ИСО). Например можно провести следующие рассуждения относительно инерциальной системы отсчета. Рассмотрим случай: с постоянной скоростью движется большой, крупный трактор при этом впереди тащит большой груз ковшом. Такое движение можно рассматривать как прямолинейное и равномерное.  Это потому что в этом случае все силы, которые действуют на тело, скомпенсированы, уравновешивают друг друга. Значит, систему отсчета, связанную с этим телом, мы можем считать инерциальной. Инерциальных систем отсчета может быть очень много. Реально же такая система отсчета все-таки идеализирована. Так что ИСО – это некая идеализация, которая позволяет эффективно моделировать реальные физические процессы. Для инерциальных систем отсчета справедлива формула сложения скоростей Галилея. Также стоит отметить, что многие системы отсчета, о которых можно говорить, можно считать инерциальными лишь в некотором приближении. Кстати, такой системой отсчета мы можем принять систему отсчета, связанную с Землей или какими-либо далекими объектами (например, со звездами). Неинерциальные системы отсчёта Большая часть систем, реальных систем отсчета – неинерциальные. Рассмотрим простой пример: сидя в поезде, вы положили на стол какое-либо тело (например, яблоко). Когда поезд трогается с места, мы будем наблюдать такую любопытную картину: яблоко будет двигаться, покатится в противоположную движению поезда сторону. В данном случае мы не сможем определить, какие же тела действуют, заставляют яблоко двигаться. В этом случае говорят, что система неинерциальная. Но можно выйти из положения, введя силу инерции. Еще один пример: когда тело движется по закруглению дороги, то возникает сила, которая заставляет отклоняться тело от прямолинейного направления движения.  В этом случае мы тоже должны рассмотреть неинерциальную систему отсчета, но, как и в предыдущем случае, тоже можем выйти из положения, вводя т.н. силы инерции. Уравнение движения центра масс В любой системе частиц имеется одна замечательная точка С- центр масс, - которая обладает рядом интересных и важных свойств. Положение точки С относительно начала начала отсчета О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:
где  - масса и радиус-вектор каждой частицы системы, M - масса всейсистемы (рис. 9).
Найдем скорость центра масс в данной системе отсчета. Продифференцировав (39) по времени, получим
Если скорость центра инерции равна нулю, то говорят, что система как целое покоится. Это вполне естественное обобщение понятия покоя отдельной частицы. Скорость же  приобретает смысл скорости движения системы как целого.Из формулы (40) следует, что
т.е. импульс системы равен произведению массы системы на скорость ее центра масс. Получим уравнение движения центра масс .Для этого продифферинцируем (41) по времени и учетем, что масса системы как таковой есть величина постоянная. Получим  (42)где  - результирующая всех внешних сил, действующих на систему.Это и есть уравнение движения центра масс системы - одно из важнейших уравнений механики. При движении любой системы частиц ее центр масс движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы, действующие на систему.  |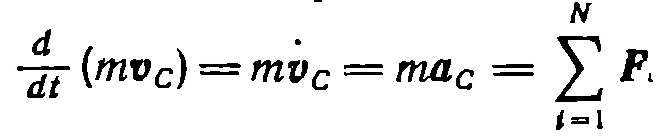
