Лабораторная работа Информационная безопасность11. лр4, Аминев. Информационная безопасность

• Название: Информационная безопасность
• Анкор: Лабораторная работа Информационная безопасность11
• Дата: 20.11.2021
• Размер: 75.66 Kb.
• Имя файла: лр4, Аминев.docx
• Тип: Лабораторная работа; #277297

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Уфимский государственный нефтяной технический университет»

Кафедра «Вычислительная техника и инженерная кибернетика»


ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ
Лабораторная работа №4

Алгоритм ассиметричного шифрования RSA

Вариант № 2


Выполнил: студент группы № БПО–19–01

очного отделения 

Аминев А.А.

(Ф.И.О. студента)

Проверил: доцент

кафедры ВТИК

Филиппова А,Г. 

   (Ф.И.О. преподавателя)
Уфа, 2021 г.

СОДЕРЖАНИЕ

1.Теоретическая часть 2

2.Практическая часть 4

2.1Задание 1. Описание порядка выполнения работы 4

2.2Задание 2. Описание порядка выполнения работы 7

3.Список литературы 8

1. Теоретическая часть

Криптография – обеспечивает сокрытие смысла сообщения с помощью шифрования и открытия его расшифрованием, которые выполняются по специальным алгоритмам с помощью ключей. Ключ – конкретное секретное состояние некоторых параметров алгоритма криптографического преобразования данных, обеспечивающее выбор только одного варианта из всех возможных для данного алгоритма. Криптоанализ – занимается вскрытием шифра без знания ключа (проверка устойчивости шифра) [3].

Кодирование – (не относится к криптографии) – система условных обозначений, применяемых при передаче информации. Применяется для увеличения качества передачи информации, сжатия информации и для уменьшения стоимости хранения и передачи.

Криптографические преобразования имеют цель обеспечить недоступность информации для лиц, не имеющих ключа, и поддержание с требуемой надежностью обнаружения несанкционированных искажений.

Большинство средств защиты информации базируется на использовании криптографических шифров и процедур шифрования - расшифрования. В соответствии со стандартом ГОСТ 28147-89 под шифром понимают совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, задаваемых ключом и алгоритмом преобразования.

В криптографии используются следующие основные алгоритмы шифрования:

− алгоритм замены (подстановки) – символы шифруемого текста заменяются символами того же или другого алфавита в соответствии с заранее обусловленной схемой замены;

− алгоритм перестановки – символы шифруемого текста переставляются по определенному правилу в пределах некоторого блока этого текста;

− гаммирование – символы шифруемого текста складываются с символами некоторой случайной последовательности;

− аналитическое преобразование – преобразование шифруемого текста по некоторому аналитическому правилу (формуле).

Процессы шифрования и расшифрования осуществляются в рамках некоторой криптосистемы [1].

Для симметричной криптосистемы характерно применение одного и того же ключа как при шифровании, так и при расшифровании сообщений. В асимметричных криптосистемах для зашифрования данных используется один (общедоступный) ключ, а для расшифрования – другой (секретный) ключ [2].

2. Практическая часть

1. Задание 1. Описание порядка выполнения работы

Алгоритм шифрования RSA (ручной расчет).

ШАГ 1. Зашифруйте сообщение андалузка с использованием калькулятора Windows (вручную).

Сообщение, предназначенное для шифрования и пары чисел для определения ключей.

Как определять из открытого ключа eзакрытый ключ d, прочтите пример (Пример 2 Процедура создания ключей).

Указания. Открытый ключ возьмите из таблицы простых чисел (таблица 1), любой на ваше усмотрение.

Таблица 1. Таблица простых чисел (из первой сотни)

3	7	11	13	17	19	23	29	31	37
41	43	47	53	59	61	67	71	73	79

ШАГ 2. Расшифруйте сообщение, закодированное Вами в предыдущем шаге. Для ее декодирования примените закрытый ключ вашей пары ключей, полученный Вами при выполнении предыдущей работы. В отчете отобразите результат расшифровки.

Первым этапом асимметричного шифрования является создание получателем шифрограмм пары ключей. Процедура создания ключей RSA заключается в следующем.

1.Выбирается два простых числа p и q, например p = 7 и q = 11

2.Вычисляется произведение n = p*q, в нашем примере n = 7*11 = 77

3.Вычисляется функция Эйлера φ(n)

φ(n) = (p-1)*(q-1)

В нашем примере φ(n) = (7-1)*(11-1) = 60. Функция Эйлера определяет количество целых положительных чисел, не превосходящих n и взаимно простых с n.

Справка. Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме 1.

4. Выбирается произвольное целое e: 0 < e < n взаимно простое с значением функции Эйлера φ(n). В нашем примере возьмём e = 7. Пара чисел (e, n) объявляется открытым ключом шифра. В нашем примере (e, n) = (7, 77)

5.Вычисляется целое число d из соотношения

(d*e) mod φ(n) = 1.

Справка. Операция mod вычисляет остаток от целочисленного деления двух чисел.

Это соотношение означает, что результатом деления произведения чисел e и d на значение функции Эйлера должно быть число 1. Поэтому d можно рассчитать по формуле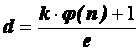

,

придавая k последовательно значения 1, 2, 3,.. до тех пор, пока не будет получено целое число d.

Подсказка. Подбор k удобнее проводить в табличном процессоре Excel.

Найдём d в рассматриваемом примере:

d = (k*60+1)/7

при k = 5, d = 43. Пара чисел (d, n) будет закрытым ключом шифра. В нашем примере (d, n) = (43, 77).

Зашифруем сообщение «андалузка» с помощью открытого ключа (7, 77)

Таблица 2. Вычисление шифрограммы

Символы исходного сообщения, Ti	Коды символов Ti (из табл.)	Зашифрованные коды символов Ci
а	1	1^7mod 77 = 1
н	15	15^7mod 77 = 71
д	5	5^7mod 77 = 47
а	1	1^7mod 77 = 1
л	13	13^7mod 77 = 62
у	21	21^7mod 77 = 21
з	9	9^7mod 77 = 37
к	12	12^7mod 77 = 12
а	1	1^7mod 77 = 1

Таким образом, мы исходное сообщение «андалузка» представили в виде шифрограммы «1, 71, 47, 1, 62, 21, 37, 12, 1».

Шифр RSA (восстановление сообщения)

Расшифровка RSA-закодированного сообщения T выполняется с помощью закрытого ключа получателя (d, n) по формуле



Рассмотрим пример восстановления исходного сообщения.

В предыдущем примере была получена пара ключей и шифрограмма «1, 71, 47, 1, 62, 21, 37, 12, 1», созданная открытым ключом данной пары.

Восстановим исходное сообщение, применив закрытый ключ (d, n) = (43, 77) той же пары.

Таблица 3. Восстановление сообщения

Зашифрованные коды символов Ci	Дешифрованные коды символов Ti (табл. 2)	Символы исходного сообщения, Ti
1	1^43 mod 77 = 1	а
71	71^43 mod 77 = 15	н
47	47^43 mod 77 = 5	д
1	1^43 mod 77 = 1	а
62	62^43 mod 77 = 13	л
21	21^43 mod 77 = 21	у
37	37^43 mod 77 = 9	з
12	12^43 mod 77 = 12	к
1	1^43 mod 77 = 1	а

Таким образом, мы восстановили исходное сообщение «андалузка».

2. 
   Задание 2. Описание порядка выполнения работы
   

Составить программу в Python (воспользуйтесь примером указанным выше). Для реализации RSA в Python, установите готовый модуль rsa. Сгенерируйте открытый и закрытый ключи. Зашифруйте вашу Фамилию. Выведите полученные открытый и закрытый ключи, а также зашифрованную вашу фамилию. Скрины приложите в отчет.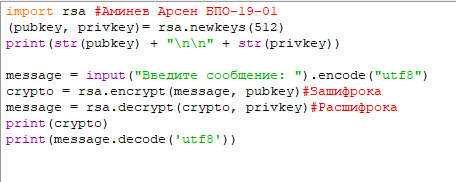



Рисунок 1 – Листинг программы на Python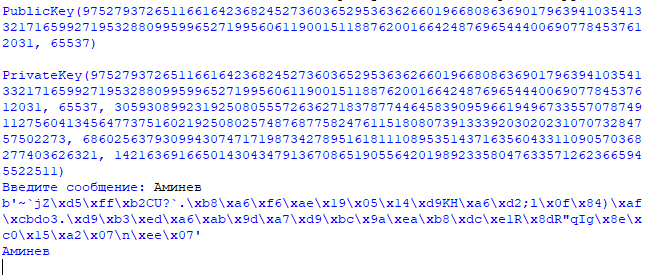



Рисунок 2 – Результаты программы на Python

3. Список литературы

1. 
   Ковалевский В., Криптографические методы. — СПб.: Компьютер Пресс.
   
2. 
   Баричев С. Г., Гончаров В. В., Серов Р. Е. Основы современной криптографии. — М.: Горячая линия — Телеком, 2002.
   
3. 
   Баричев С. Введение в криптографию. Электронный сборник. Вече1998.