золтое сечение в жизни. проект З 2 docx. Информационный блок Название темы исследования Золотое сечение
 Скачать 131.83 Kb. Скачать 131.83 Kb.
|
|
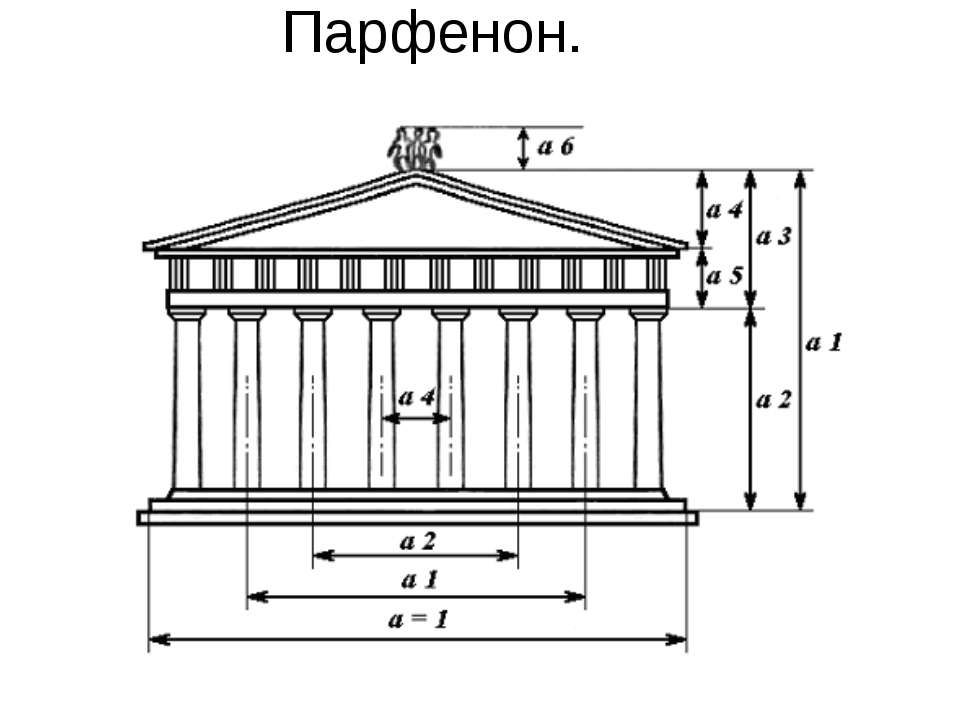
«Золотое сечение» в жизни. Речица 2023 «Геометрия владеет двумя сокровищами: одно из них — теорема Пифагора, другое — деление отрезка в среднем и крайнем отношении» (Иоганн Кеплер) Информационный блок 1.1. Название темы исследования «Золотое сечение» в жизни. 1.2 Актуальность исследования обусловлена интересом к духовному наследию белорусского народа, возможностью глубже понять такое направление в архитектуре как православное зодчество, а также интересом к последовательности чисел Фибоначчи и «золотому сечению» в православной архитектуре. 1.3 Цель работы: установить закономерность ряда Фибоначчи, исследовать его интересные свойства, выявить гармоничность постройки собора Успения Пресвятой Богородицы в г. Речице с точки зрения «золотого сечения». 1.4 Задачи : найти связь с золотым сечение исследовать пропорции в архитектуре собора Пресвятой Богородицы в г. Речице. провести математические расчеты в вычислении пропорций «золотого сечения»; обобщить полученные результаты. 2.Описание исследовательской работы 2.1 Ведущая идея исследования Золотое сечение – понятие математическое, но оно является критерием гармонии и красоты. Почему нас так привлекают строения древней архитектуры, при виде котрых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье и в современном мире. Одним из красивейших произведений древнегреческой архитектуры является Парфенон Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада. Другим примером из архитектуры древности является Храм Афины на Акрополе был построен в V веке до н.э. под руководством знаменитого греческого архитектора Фидия. Он был разрушен в 1687 году, затем частично восстановлен
«Золотое сечение, или божественная пропорция (лат. Sectio aurea; Sectio Divina; см. золото; пропорционирование) - идеальное соотношение величин, наилучшая и единственная пропорция, уравновешивающая отношения частей какой-либо формы между собой и каждой части с целым, основа гармонии». Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей. Или, другими словами, меньший отрезок относится так относится к большему, как больший ко всему отрезку. 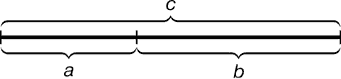 a:b=b:c Итальянский математиком средневековья Леонардо Пизанским. Более известный под именем Фибоначчи. Открыл последовательность чисел, которые представляют собой крайне интересную систему, последовательность имеет следующий вид... 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 ,987, 1597, 2584, 4181, 6765... Каждое следующее число получается путем суммирования двух предыдущих 0+1=1 1+1=2 2+1=3 В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности, на число стоящее перед ним, результатом будет всегда величина 1,618 Его еще называют число Фибоначи 233/144=1.618 377 /233 = 1.618 «Золотая пропорция» равна соотношению единицы к 1,618, 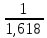 ≈ 0.618 ≈ 0.618В научной литературе по исследованию памятников архитектуры Древней Руси выявлены общепризнанные образцы гармонического единства, лучшие создания человеческого гения: церковь Вознесения села Коломенского под Москвой (построена в 1532 г); церковь Покрова на Нерли (1165 - 1167 гг.). Среди памятников древней Руси, кроме указанных, к шедеврам архитектуры относятся: Успенский собор Печорского монастыря в Киеве, Успенская церковь Елецкого монастыря в Чернигове. 2.2.Описание сути исследования Из истории храма известно строительство Собора Успения Пресвятой Богородицы в г. Речице началось еще в 18 веке. Изначально это было деревянное строение Воскресенской церкви. Возведение самого собора началось в 1842г. Уже в следующем году, в ночь с 28 на 29 октября строящаяся при нем колокольня неожиданно разрушилась и, падая, повредила церковь почти до основания. Недобросовестный подрядчик исчез. Денег на строительство не осталось. Храм простоял в руинах более 20 лет. В 1864 г. подряд на строительство храма получил минский купец и городской глава Свечников. Казалось, святыня снова восстанет из руин, но в 1866 г. Свечников неожиданно обанкротился, и строительные работы приостановили. И только через шесть лет 1872 г. соборный храм был освящен Преосвященным Александром, епископом Минским и Бобруйским, в честь Успения Пресвятой Богородицы. Событие было отмечено великим князем Александром Александровичем (будущим императором Александром III), который передал Речицкому храму позолоченную дарохранительницу. В 1934 г. Успенский собор закрыли. В 1940 г. храм и пристройка были поражены пожаром. В конце 1941 г. силами верующих, в храме был проведен ремонт и начались богослужения до 1947 г.. В 1999 г. решением горисполкома здание собора было передано городскому православному приходу. Во все времена люди пытались находить закономерность в окружающем мире. Наше исследование это исследование «математического каркаса» Собора Успения Пресвятой Богородицы в г. Речице. Наш вопрос: существует ли закономерность ряда Фибоначчи, его интересные свойства - в православной архитектуре Собора Успения Пресвятой Богородицы в г. Речице. Расчет основных размеров определили по фотографиям, и строительным чертежам, которые нам предоставил протоирей Алексей Васильевич Пешко. Исследование математического каркаса собора Храм имеет крестово-купольное строение. Основа храма - прямоугольный параллелепипед ( восьмерик на четверик). Первое что мы сделали это все основные размеры разделили на число ФИБОНАЧИ. Обозначим: АР = 7,20 7.20 : 1.618 ≈4 Нижнюю часть храма АМ АМ=15 15 : 1.618 ≈9 Нижнюю часть храма до колокольни АК АК= 20,80 20.80 : 1.618 ≈13 высоту храма до верхней точки креста купола АD АД=37 37: 1.618 ≈22 Получился ряд Фибоначи, 4; 9; 13; 22 архитектор использовал свою гармоничную систему пропорционирования, приближенно равную «золотой пропорции» Найдем отношение ширины храмовой части к ее высоте: 12,30 : 20 ≈0,615 Определили высоту основной части храма и обозначим её АВ: АВ= 24,80 Определили высоту храма с куполом и обозначим её АС: АС=34,24 Определили высоту храма до верхней точки креста купола и обозначим её АД: АД=37 BD= 12,2 2.Найдём отношение основной части храма AК к высоте всего храма AС, и отношение BD к АВ: АК/АС=20,80/34,04= 0,611 КС/АК = 13,24/20,80=0,636 Видно, что это отношение приближенно является «золотой пропорцией». 3.Найдем отношение нижней части храма до карниза АМ к высоте до второго карниза АМ/АВ =15/24,80=0,604 МВ/АМ =9,80/15/=0,653 Видно, что это отношение приближенно является «золотой пропорцией» Теперь исследуем купол 1.Высота купола ОС = 4,5, а высота креста СD=2,76 Найдем отношение ОC / ОD=4,5/7,3=0,616 ДC / ОD=2,76/4,5=0,613 близка к «золотой» пропорции 2. Отношение Высота шатра с куполом к высоте купола с крестом МД/ОД=7,30/12=0,608 близка к «золотой» пропорции. Проведя множество расчетов мы пришли к выводу, что пропорции всего храма и верхней части совпадают, хотя и не являются «золотыми», именно это и придаёт храму неповторимую архитектурную гармонию, так же заложена система пропорций, в которой встречаются функции «Золотого сечения» 2.3.Результативность и эффективность опыта Исследовала систему пропорций в архитектуре и выявили гармоничность постройки собора Успения Пресвятой Богородицы в г. Речице В ходе исследовательской работы, я осуществила поиск и отбор информации о «золотом сечении» и его свойствах, имеющих значение в архитектуре, православном зодчестве. На основании полученных фактов сделали вывод: что в архитектуре православного собора заложена гармоничная система пропорций, соответствующая «золотому сечению». Заключение Согласно цели исследовательской работы я познакомилась с числами Фибоначчи. Числа Фибоначчи – это красиво, серьёзно, актуально Числа Фибоначчи имеют различное проявление в природе, архитектуре. При выполнении работы мы убедились, что природа сама творит красоту по законам математики Почему православные храмы так притягательны для верующих и неверующих? Храм - это прежде всего общественное место, нередко праздничное, предмет постоянной заботы и гордости местных жителей. Его архитектура выражает идеал красоты, в ее образах воплощается духовное совершенство. Созерцая храмы – эти творения русской души, соединяешься с ними в едином порыве к красоте и духовному свету Список литературы. Энциклопедия для детей. Т. 11. Математика /Глав. ред. М. Д. Аксёнова; метод. и отв. ред. В. А. Володин. – М.: Аванта+, 2003. – 668 с. Шевелев И. Ш.. Геометрическая гармония. Опыт исследования пропорций в архитектуре; - Кострома: Полиграфиздат, 1963 г. -109с. Плужников В.И. Термины российского архитектурного наследия: Словарь-глоссарий; — М.: «Искусство», 1995. – 159 с. Раппорт П.А. Древнерусская архитектура: науч. изд.- СПб.: Строй – издат. С.-Петербургское отд-ние, 1993.-287 с. http://decopedia.homeideas.ru/архитектура http://nauka.relis.ru/52/0306/52306082.htm Математические досуги. Золотая пропорция. Новый взгляд. Перельман Я. И.Занимательная геометрия / Я. И. Перельман. Под ред. и с доп. Б. А. Кордемского. - Изд. 7 – е перераб.– М.:Государственное издательство технико – теоретической литературы, 1986. – 308 http://yspenie-rechica.cerkov.ru/ Официальный сайт прихода собора Успения Пресвятой Богородицы в г. Речице http://youtube.com/watch «Числа и формула Фибоначчи». «Золотое сечение». К понятию о Золотом сечении / О. В. Максименко, В. С. Пастор, П. В. Ворфоломеева [и др.]. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 35-39. — URL: https://moluch.ru/young/archive/9/619/ |