Главная страница
Навигация по странице:

  • «МИРЭА – Российский технологический университет» РТУ МИРЭА

  • ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ №11 Синтез четырехразрядного счетчика с параллельным переносом между разрядами четырьмя способамипо дисциплине

    		•

    11.Лабораторная работа №3(ИНБО-07-18). Информатика


    Скачать 0.66 Mb.
    НазваниеИнформатика
    Анкор11.Лабораторная работа №3(ИНБО-07-18).docx
    Дата06.12.2020
    Размер0.66 Mb.
    Формат файлаdocx
    Имя файлаInf_praktika_11_Bulaev_FIN.docx
    ТипОтчет
    #157639



    МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

    Федеральное государственное бюджетное образовательное учреждение

    высшего образования

    «МИРЭА – Российский технологический университет»
    РТУ МИРЭА


    Институт информационных технологий (ИТ)

    Кафедра общей информатики (ОИ)
    ОТЧЕТ

    ПО ПРАКТИЧЕСКОЙ РАБОТЕ №11

    Синтез четырехразрядного счетчика с параллельным переносом между разрядами четырьмя способами

    по дисциплине

    «ИНФОРМАТИКА»


    Выполнил студент группы ИКБО-22-20 Булаев А. П.
    Принял доцент кафедры ОИ, к.т.н. Воронов Г. Б.

    Практическая «__»_______2020 г.

    работа выполнена

    «Зачтено» «__»_______2020 г.

    Москва 2020

    СОДЕРЖАНИЕ


    Постановка задачи и персональный вариант 3

    Восстановленная таблица истинности 3

    Проектирование оптимальных схем управления триггерами 4

    Реализация счетчика с оптимальной схемой управления 10

    Реализация счетчика на преобразователе кодов 11

    Выводы 12

    Список информационных источников 12



    Постановка задачи и персональный вариант


    Разработать счетчик с параллельным переносом на D-триггерах двумя способами:

    • с оптимальной схемой управления, выполненной на логических элементах общего базиса;

    • со схемой управления, реализованной на преобразователе кодов (быстрая реализация, но не оптимальная схема).

    В качестве исходных данных использовать индикатор CNT лабораторного комплекса, на котором слева направо отображены:

    • направление счета (0 —сложение, 1 —вычитание);

    • максимальное значение счетчика (не путать с модулем счета);

    • шаг счета.

    Протестировать работу схемы и убедиться в ее правильности.

    Персональный вариант: 095

    Восстановленная таблица истинности


    Имеются следующие исходные данные:

    • направление счета - сложение;

    • максимальное значение счетчика – 9;

    • шаг счета - 5.

    По исходным данным восстановим таблицу переходов счетчика (таблица 1).

    Таблица 1. Таблица переходов счётчика

    Q3(t)
    Q2(t)
    Q1(t)
    Q0(t)
    Q3(t+1)
    Q2(t+1)
    Q1(t+1)
    Q0(t+1)

    0
    0
    0
    0
    0
    1
    0
    1

    0
    0
    0
    1
    0
    1
    1
    0

    0
    0
    1
    0
    0
    1
    1
    1

    0
    0
    1
    1
    1
    0
    0
    0

    0
    1
    0
    0
    1
    0
    0
    1

    0
    1
    0
    1
    0
    0
    0
    0

    0
    1
    1
    0
    0
    0
    0
    1

    0
    1
    1
    1
    0
    0
    1
    0

    1
    0
    0
    0
    0
    0
    1
    1

    1
    0
    0
    1
    0
    1
    0
    0

    1
    0
    1
    0
    *
    *
    *
    *

    1
    0
    1
    1
    *
    *
    *
    *

    1
    1
    0
    0
    *
    *
    *
    *

    1
    1
    0
    1
    *
    *
    *
    *

    1
    1
    1
    0
    *
    *
    *
    *

    1
    1
    1
    1
    *
    *
    *
    *



    Проектирование оптимальных схем управления триггерами


    Таблица переходов является частично определенной: состояния 1010, 1011, 1100, 1101, 1110 и 1111 согласно исходным данным возникать никогда не должны, поэтому очередное состояние Q(t+1) для этих случаев мы можем интерпретировать как нам удобно в целях минимизации управляющей логики. Рассматриваем столбцы Qi(t+1) как самостоятельные функции от четырех переменных и проводим их минимизацию. Также нам необходимо для каждой функции из двух возможных минимальных форм выбрать самую короткую. Допустим, начнем с функции Q3(t+1). Оценим сложность минимальных форм, которые для нее получатся, по количеству переменных, входящих в них, и выберем оптимальную форму. Для этого построим необходимые карты Карно.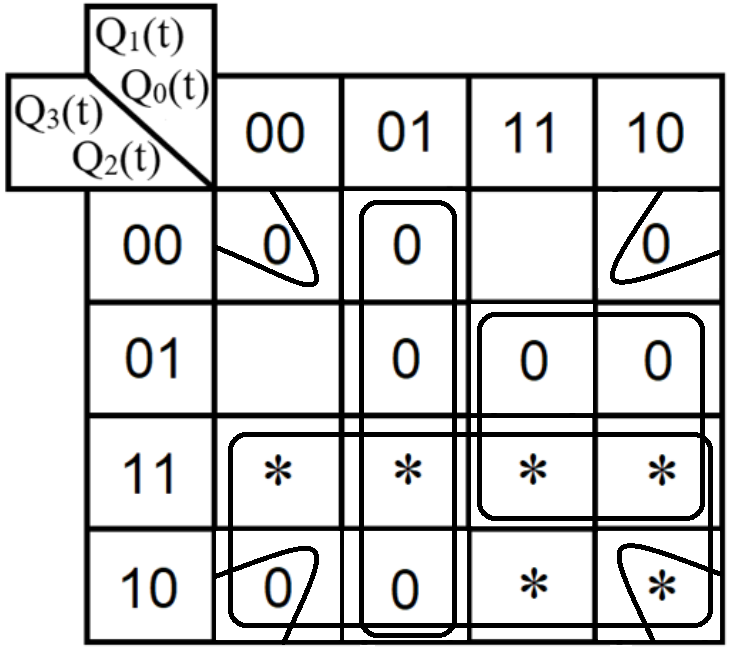



    Рисунок 1 – Карта Карно для МКНФ функции Q3(t+1)
    Оценим сложность возможной формулы МДНФ. Из карты Карно (см. рис. 1) видно, что в нашем случае МКНФ Q3(t+1) будет описана при помощи 1 + 2 + + 2 + 2 = 7 переменных либо их отрицаний.

    Проделаем аналогичную операцию для МДНФ этой же функции. Возьмем за основу уже построенную карту Карно (см. рис. 1), ведь на всех пустых клетках там стоят единицы. Для наглядности удалим нулевые значения. Попытаемся интерпретировать звездочки как единичные значения функции. Выделим интервалы, получится следующая карта Карно (см. рис. 2).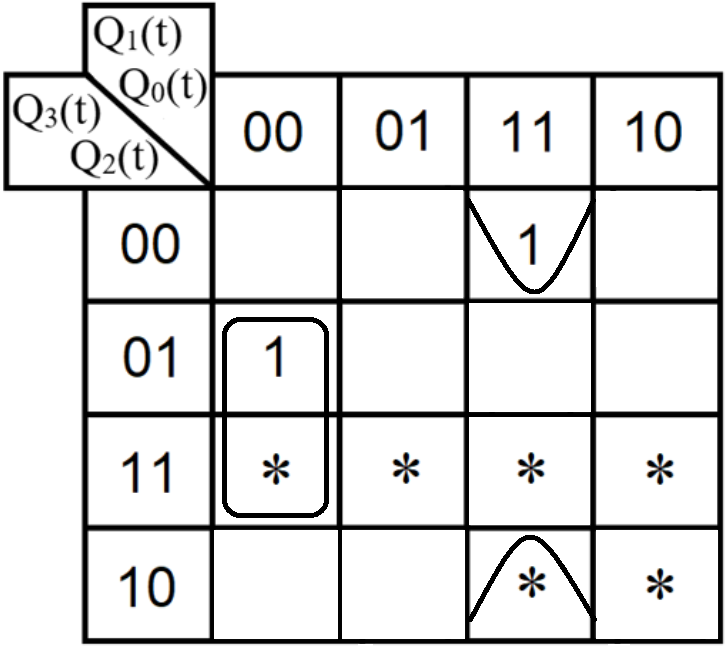



    Рисунок 2 - Карта Карно для МДНФ функции Q3(t+1)
    Оценим сложность МДНФ функции Q3(t+1): 3 + 3 = 6.

    Делаем вывод, что МДНФ функции Q3(t+1) строить выгоднее, чем МКНФ.

    Запишем формулу для МДНФ функции Q3(t+1) (формула 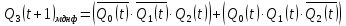1):

    (1)
    Далее, аналогично рассмотрим функцию Q2(t+1). Построим карту Карно для МДНФ функции Q2(t+1) и проведем оценку сложности.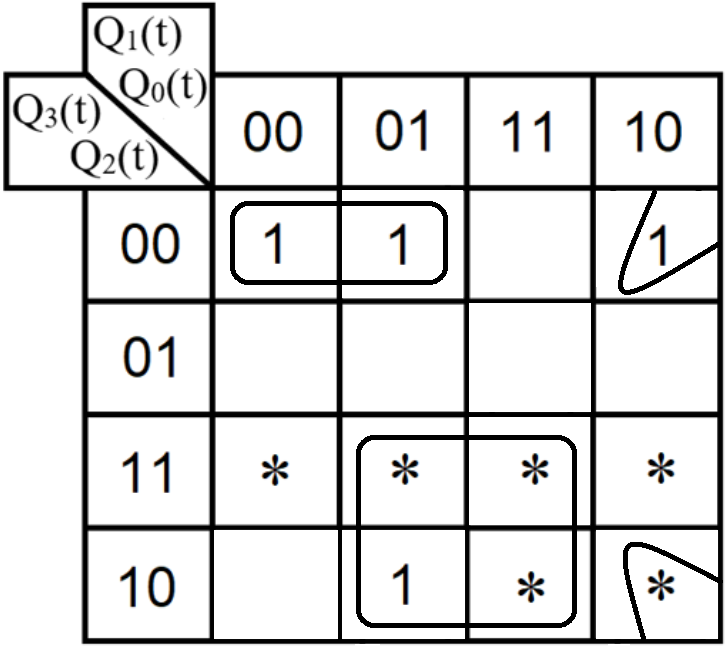



    Рисунок 3 - Карта Карно для МДНФ функции Q2(t+1)
    Оценим сложность возможной формулы МДНФ. Из карты Карно (см. рис. 3) видно, что в нашем случае МДНФ Q2(t+1) будет описана при помощи 2 + 3 + + 3 = 8 переменных либо их отрицаний.

    Проделаем аналогичную операцию для МКНФ этой же функции. Возьмем за основу уже построенную карту Карно (см. рис. 3), ведь на всех пустых клетках там стоят нули. Для наглядности удалим единичные значения. Попытаемся интерпретировать звездочки как нулевые значения функции. Выделим интервалы, получится следующая карта Карно (см. рис. 4).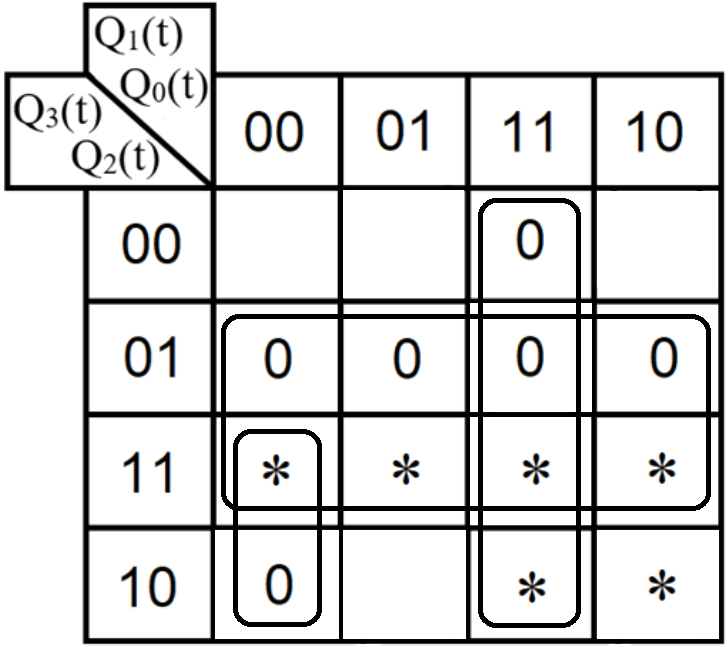


    Рисунок 4 – Карта Карно для МКНФ функции Q2(t+1)
    Оценим сложность МКНФ функции Q2(t+1): 1 + 2 + 3 = 6.

    Делаем вывод, что МКНФ функции Q2(t+1) строить выгоднее, чем МДНФ.

    Запишем формулу для МКНФ функции Q2(t+1) (формула 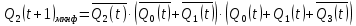2):

    (2)
    Далее, аналогично рассмотрим функцию Q1(t+1). Построим карту Карно для МДНФ функции Q1(t+1) и проведем оценку сложности.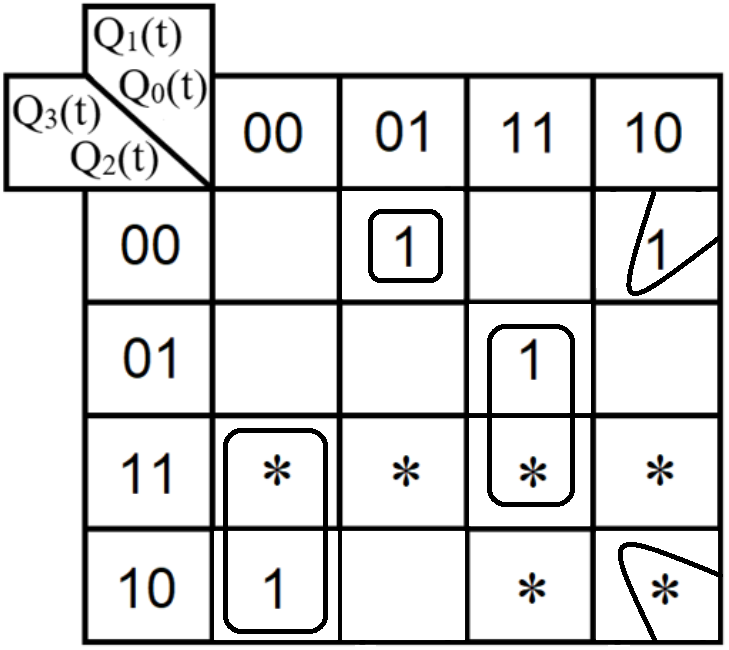


    Рисунок 5 - Карта Карно для МДНФ функции Q1(t+1)
    Оценим сложность возможной формулы МДНФ. Из карты Карно (см. рис. 5) видно, что в нашем случае МДНФ Q1(t+1) будет описана при помощи 3 + 3 + + 3 + 4 =13 переменных либо их отрицаний.

    Проделаем аналогичную операцию для МКНФ этой же функции. Возьмем за основу уже построенную карту Карно (см. рис. 5), ведь на всех пустых клетках там стоят нули. Для наглядности удалим единичные значения. Попытаемся интерпретировать звездочки как нулевые значения функции. Выделим интервалы, получится следующая карта Карно (см. рис. 6).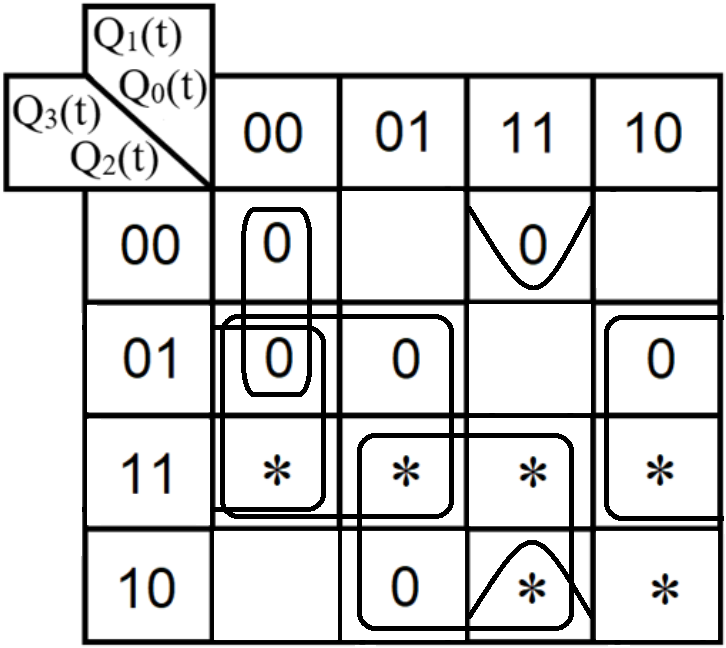


    Рисунок 6 - Карта Карно для МКНФ функции Q1(t+1)
    Оценим сложность МКНФ функции Q1(t+1): 2 + 2 + 2 + 3 + 3 = 12.

    Делаем вывод, что МКНФ функции Q1(t+1) строить выгоднее, чем МДНФ.

    Запишем формулу для МКНФ функции Q1(t+1) (формула 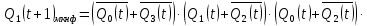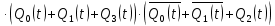3):



    (3)

    Реализация счетчика с оптимальной схемой управления


    При помощи полученных формул выполним реализацию схем управления триггеров счетчика (см. рис. 7).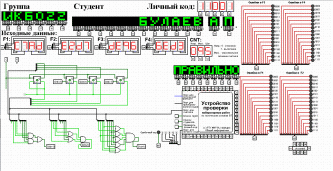



    Рисунок 7 - Схема счетчика с подключением к устройству проверки

    Тестирование показало правильность работы схемы.

    Реализация счетчика на преобразователе кодов


    Выполним быструю реализацию счетчика при помощи преобразователя кодов в качестве схемы управления триггерами. Здесь не требуется никакая минимизация, необходимо просто по таблице переходов правильно соединить выходы дешифратора со входами шифратора. Таким образом, можно сразу построить схему счетчика (рис.8).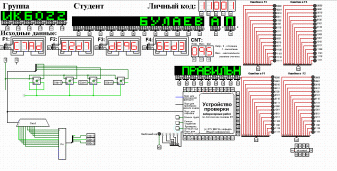


    Рисунок 8 – Счетчик со схемой управления, выполненной на преобразователе кодов

    Тестирование показало, что схема работает правильно.

    Выводы


    В ходе практической работы был разработан счетчик с параллельным переносом на D-триггерах двумя способами: с оптимальной схемой управления, выполненной на логических элементах общего базиса и со схемой управления, выполненной на преобразователе кодов. Разработанные счётчики были построены в лабораторном комплексе. Тестирование показало правильность работы схем.

    Список информационных источников


    1. Информатика: Методические указания по выполнению практических работ / С.С. Смирнов, Д.А. Карпов – М., МИРЭА – Российский технологический университет, 2020. –102с.

    2. Лекции. Информатика. Смирнов С. С., МИРЭА – Российский технологический университет, 2020.

    3. Logisim – графический инструмент для разработки и моделирования логических схем [Электронный ресурс] URL: http://www.cburch.com/logisim/ru/ (Последнее обращение 19.11.2020)

    написать администратору сайта