Главная страница
Навигация по странице:

  • 1. Переключательные функции

  • 2. Переключательные функции одного и двух переменных

  • 4. Аналитическая запись переключательной функции

  • 5. Преобразования логических выражений

  • 6. Знакомство с программой «ЕВЕМА-2» Программа «

  • Порядок выполнения работы Содержанием работы является: аналитическая запись всех 16 переключательных функций 2-х аргументов, построение схем с использованием программы «

  • Пример выполнения лабораторной работы

    		•

    Лабраб№1. Лабораторная работа 1 логические основы информатики. Построение комбинационных схем на логических элементах


    Скачать 441.5 Kb.
    НазваниеЛабораторная работа 1 логические основы информатики. Построение комбинационных схем на логических элементах
    АнкорЛабраб№1.doc
    Дата21.07.2018
    Размер441.5 Kb.
    Формат файлаdoc
    Имя файлаЛабраб№1.doc
    ТипЛабораторная работа
    #21771

    Лабораторная работа № 1

    ЛОГИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ.

    ПОСТРОЕНИЕ КОМБИНАЦИОННЫХ СХЕМ

    НА ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ
    Цель работы. Изучение переключательных функций 1-го и 2-х аргументов и комбинационных схем на логических элементах

    1. Переключательные функции

    Переключательной (или булевой) функцией (ПФ) называется функция, способная принимать лишь два значения 0 и 1, и такая, что все ее аргументы также могут принимать только два значения 0 и 1.

    Любая ПФ может быть задана таблицей ее значений в зависимости от значений ее аргументов. Эту таблицу называют таблицей истинности ПФ.

    Пример 1.1. Зададим ПФ трех аргументов f(x1, x2, x3). Так как каждый из аргументов принимает лишь 2 значения, поэтому мы имеем 8 различных комбинаций 3 переменных. Эти комбинации называют наборами. Наборы обычно пишут в так называемом естественном порядке, когда наборы принимают значения (000), (001), …, (111). Для получения следующего набора прибавляют 1 к правому разряду – применяется как бы сложение чисел.

    Наборам присваивается номер, равный двоичному числу, соответствующему данному набору. Сопоставляя каждому набору одно из двух значений ПФ, мы и получим таблицу истинности (например, представленную в табл. 1).

    Таблица 1

    х1
    х2
    х3
    f

    0
    0
    0
    1

    0
    0
    1
    1

    0
    1
    0
    0

    0
    1
    1
    1

    1
    0
    0
    0

    1
    0
    1
    0

    1
    1
    0
    1

    1
    1
    1
    0

    2. Переключательные функции одного и двух переменных

    Рассмотрим некоторые ПФ одного и двух аргументов. В табл.2 представлены все 4 функции одного аргумента. Таблица 2

    x
    f0(x)
    f1(x)
    f2(x)
    f3(x)

    0
    0
    0
    1
    1

    1
    0
    1
    0
    1


    Функция f0 (x) равно нулю (константа нуля), f3(x) равна единице (константа единицы), функция f1(x) повторяет значение аргумента, т.е. f1(x) = x. Наиболее интересной и имеющей важное значение является функция f2(x), которая принимает значения, обратные значению аргумента – логическое отрицание или функция НЕ и обозначается как:

    = ù х (читается не х).

    Все ПФ двух аргументов приведены в табл.3.

    Таблица 3

    х1
    х2
    f0
    f1
    f2
    f3
    f4
    f5
    f6
    f7
    f8
    f9
    f10
    f11
    f12
    f13
    f14
    f15

    0
    0
    0
    0
    0
    0
    0
    0
    0
    0
    1
    1
    1
    1
    1
    1
    1
    1

    0
    1
    0
    0
    0
    0
    1
    1
    1
    1
    0
    0
    0
    0
    1
    1
    1
    1

    1
    0
    0
    0
    1
    1
    0
    0
    1
    1
    0
    0
    1
    1
    0
    0
    1
    1

    1
    1
    0
    1
    0
    1
    0
    1
    0
    1
    0
    1
    0
    1
    0
    1
    0
    1



    Функции f0(x1,x2) и f15(x1,x2) не зависят от значений аргументов: f0(x1,x2)=0 и f15(x1,x2)=1. Функции f3(x1,x2), f5(x1, x2), f10(x1,x2) и f12(x1,x2) являются фактически функциями одного аргумента:

    f3(x1,x2)=x1, f5(x1,x2)=x2, f10(x1,x2)=x2 и f12(x1,x2)=x1.

    Рассмотрим часто встречающиеся ПФ. Функция f1(x1,x2) реализует операцию конъюнкции или логического произведения. Как видим из табл. 3, функция f1(x1,x2) равна 1, когда и x1 и x2 равны 1. Конъюнкция обозначается как

    f1(x1,x2)=x1  x2 = x1  x2 = x1 x2 (читается x1 и x2).

    Функция f7(x1,x2) реализует операцию дизъюнкцию или логического сложения. Функция равна 1, когда или x1 или x2 равны 1. Дизъюнкция обозначается как

    f7(x1,x2)=x1  x2.

    Функция f14(x1,x2) реализует операцию отрицания конъюнкции. Из табл. 3 видно, что когда конъюнкция f1(x1,x1) равна 0, то функция f14(x1,x2) равна 1, а если f1(x1, x2) равна1, то f14(x1,x2) равна 0, т.е. f14(x1,x2)=f1(x1,x2). Эта операция получила название “штрих Шеффера” и обозначается различными способами:





    Функция f8(x1, x2) реализует операцию отрицания дизъюнкции. По аналогии с функцией отрицания конъюнкции, из табл.3 видно, что f8(x1, x2)=f7(x1, x2). Эта операция также получила отдельное название – “стрелка Пирса” и обозначается следующим образом:





    Функция f6(x1, x2) реализует операцию логической неравнозначности или еще ее называют суммой по модулю два. ПФ равна 1, если аргументы x1 и x2 не равны между собой.

    Остальные ПФ двух аргументов рассматривать пока не будем.

    3. Логические элементы

    Рассмотрим некоторые логические элементы с одним и двумя входами, реализующие ПФ от одного и двух аргументов.

    Логический элемент НЕ (инвертор). Условное обозначение элемента НЕ представлено на рис. 1:



    Рис.1. Обозначение логического элемента НЕ
    Операция дизъюнкции y = x1 v x2 v ... v xn, n 2, выполняется элементом ИЛИ. Сигнал на выходе элемента ИЛИ принимает значение 0 только в том случае, если ни один из входных сигналов не имеет в данный момент времени значения 1. Условное обозначение элемента ИЛИ представлено на рис. 2:



    Рис.2. Обозначение логического элемента ИЛИ

    Операция конъюнкции y = x1 x2 ... xn, n 2, выполняется элементом И, сигнал на выходе которого равен 1, если все входные сигналы одновременно равны 1. Условное обозначение элемента И представлено на рис. 3:



    Рис.3. Обозначение логического элемента И

    Операцию отрицания дизъюнкции реализует элемент ИЛИ-НЕ, представляющий собой последовательное соединение элемента ИЛИ с элементом НЕ. Условное обозначение элемента ИЛИ-НЕ представлено на рис. 4.



    Рис.4. Обозначение элемента ИЛИ-НЕ

    Операцию отрицания конъюнкции реализует элемент И-НЕ, представляющий собой последовательное соединение элемента И с элементом НЕ. Условное обозначение элемента И-НЕ представлено на рис. 5:



    Рис.5. Обозначение элемента И-НЕ

    4. Аналитическая запись переключательной функции

    Для аналитического представления ПФ используют правило ее записи по единицам:

    – в таблице истинности выбирают все наборы, на которых ПФ равна единице;

    – выписывают произведения аргументов, соответствующих этим наборам. При этом, если в этом наборе аргумент равен 1, то он вписывается в произведение без изменения, если же он равен 0, то он вписывается со знаком отрицания;

    – все полученные произведения соединяются знаком дизъюнкции.

    5. Преобразования логических выражений

    Построение комбинационных схем связано с преобразованиями логических выражений, которые содержат ПФ. Приведем достаточно очевидные формулы, содержащей операции дизъюнкции, конъюнкции и отрицания.

    Ф

    ормулы для отрицания    :
    Формулы для дизъюнкции:








    Формулы для конъюнкции:




    Правило действия со скобками:




    Операция поглощения:




    Операция склеивания:





    Формулы де Моргана:





    Приведенные соотношения дают правила преобразования логических выражений, с помощью которых получают эквивалентные выражения. Новые выражения могут оказаться проще, а это приведет к экономии оборудования и повышению быстродействия устройств ЭВМ.

    6. Знакомство с программой «ЕВЕМА-2»

    Программа «ЕВЕМА-2» позволяет собрать в электронном виде комбинационную схему и схемы различных устройств ЭВМ и проверить их работоспособность и функционирование.

    1. Порядок выполнения работы

    Содержанием работы является: аналитическая запись всех 16 переключательных функций 2-х аргументов, построение схем с использованием программы «ЕВЕМА-2» и контроль правильности их работы.

    Работу рекомендуется выполнять в следующей последовательности:

    - представить заданные переключательные функции 2-х аргументов в булевом базисе;

    - набрать на компьютере комбинационную схему;

    - проверить правильность работы схемы, задавая на ее входах всевозможные наборы значений переменных.

    1. Пример выполнения лабораторной работы

    Построить схему сумматора по модулю два на элементах булевого базиса (И, ИЛИ, НЕ).

    По таблице истинности для ПФ f6(x1,x2) логической неравнозначности в соответствии с правилом записи ПФ по единицам получим:




    Тогда схема сумматора по модулю два будет иметь вид: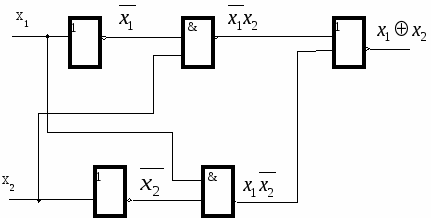

    Рис. 6. Схема сумматора по модулю два на элементах И, ИЛИ, НЕ

    Эта схема имеет 3 уровня. Собрав на компьютере комбинационную схему с использованием программы «ЕВЕМА-2» и включив ее питание, проводим контроль правильности ее работы.

    9. Cодержание отчета

    1. Таблица истинности переключательных функций 2-х аргументов,

    2. Аналитическая запись заданных переключательных функций 2-х аргументов.

    3. Построение схем с использованием программы «ЕВЕМА-2» и контроль правильности их работы.


    10. Задания

    1. Записать в аналитическом виде переключательные функции f1(x1, x2), f7(x1, x2), f13(x1, x2) и f14 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    2. Записать в аналитическом виде переключательные функции f1(x1, x2), f8(x1, x2), f11(x1, x2) и f13 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    3. Записать в аналитическом виде переключательные функции f3(x1, x2), f6(x1, x2), f10(x1, x2) и f15 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    4. Записать в аналитическом виде переключательные функции f5(x1, x2), f6(x1, x2), f9(x1, x2) и f11 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    5. Записать в аналитическом виде переключательные функции f4(x1, x2), f6(x1, x2), f13(x1, x2) и f15 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    6. Записать в аналитическом виде переключательные функции f6(x1, x2), f7(x1, x2), f10(x1, x2) и f12 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    7. Записать в аналитическом виде переключательные функции f3(x1, x2), f8(x1, x2), f10(x1, x2) и f13 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    8. Записать в аналитическом виде переключательные функции f5(x1, x2), f6(x1, x2), f13(x1, x2) и f15 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    9. Записать в аналитическом виде переключательные функции f3(x1, x2), f6(x1, x2), f10(x1, x2) и f14 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    10. Записать в аналитическом виде переключательные функции f5(x1, x2), f8(x1, x2), f6(x1, x2) и f14 (x1, x2). Построить схемы с использованием программы «ЕВЕМА-2» и проверить правильности их работы.

    11. Контрольные вопросы

    1. Что такое переключательная функция?

    2. Как задается переключательная функция?

    3. При каких значениях аргументов переключательная функция конъюнкция равна 1?

    4. При каких значениях аргументов переключательная функция дизъюнкция равна 1?

    5. При каких значениях аргументов переключательная функция логической неравнозначности (сложение по модулю два) равна 1?

    6. Чему равна функция ?

    7. Чему равна функция ?

    8. Чему равна функция ?

    9. Чему равна функция ?

    10. Чему равна функция ?

    Литература

    1. Конспект лекций по дисциплине «Информатика» в электронном виде.

    написать администратору сайта