Курсовая Расчёт характеристик направленности линейной антенны. Курсовой Титов. Инженерная школа
 Скачать 233.89 Kb. Скачать 233.89 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Дальневосточный федеральный университет» ИНЖЕНЕРНАЯ ШКОЛА Кафедра Приборостроения Параскев Аркадий Иванович РАСЧЕТ ХАРАКТЕРИСТИК НАПРАВЛЕННОСТИ ЛИНЕЙНОЙ АНТЕННЫ вариант № 2.7.5 КУРСОВАЯ РАБОТА по дисциплине «Теория направленного излучения» Студент группы ___________
г. Владивосток 2019 ОглавлениеВведение 4 Исходные данные 5 Вывод формулы характеристики направленности 6 Определение расстояния между элементами 6 Направленные свойства АР на разных частотах 8 Сравнение направленных свойств заданной дискретной базы и сплошной полосы 11 Заключение 13 Список литературы 14 ВведениеДля получения большей мощности излучения, обеспечения направленности и возможности управления направленностью без изменения конструкции или механического поворота используют антенны, имеющие много преобразователей и большие волновые размеры. Такие многоэлементные антенны, состоящие и ненаправленных преобразователей, размеры которых малы по сравнению с длиной волны, получили название антенных решёток. Исходные данныеЛинейная эквидистантная антенная решётка (АР) из 5 ненаправленных элементов имеет, с углом компенсации, амплитудное распределение представленное на рис. 1. 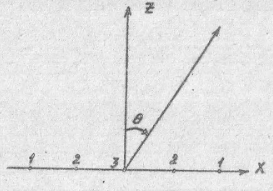 Рисунок 1 – Чертеж антенны Исходные данные для расчета приведены в таблице 1. Таблица 1 – Исходные данные для расчета
Вывод формулы характеристики направленностиПоскольку антенная решётка имеет не равномерную амплитудное распределение, необходимо применить теорему сложения. Согласно теореме сложения характеристика направленности групповой АР может быть представлена в виде суммы характеристики направленности отдельных N групп ее элементов с коэффициентами Mj, равными отношению нормирующего множителя соответствующей группы к нормирующему множителю характеристики направленности всей АР: 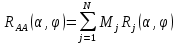 ,(1) ,(1)где 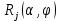 – ДН j-й группы; – ДН j-й группы; 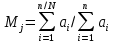 ; ; 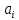 – амплитуда i-го элемента, n – числа элементов AA. – амплитуда i-го элемента, n – числа элементов AA.Разобьем заданную АР на 3 группы. Первая группа состоит из одного ненаправленного элемента, из этого следует что характеристика направленности во всех направлениях будет равна единице. Вторая и третья группа состоит из двух элементов. 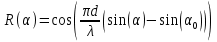 ,(2) ,(2)где 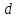 – расстояние между элементами; – расстояние между элементами; 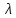 – длина волны; – длина волны; 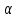 – наблюдения; – наблюдения; 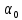 – угол компенсации. – угол компенсации.Формула (2) применяется для расчёта АР состоящей из двух ненаправленных элементов. Используем формулу (1) для расчёта характеристики направленности второй и третьей группы, а также применив теорему сложения для расчёта АР, получим формулу для характеристики направленности заданной антенны:  ,(3) ,(3)Определение расстояния между элементамиПо условию задания, боковые максимумы диаграммы направленности не должны превышать значения σ. Для этого необходимо подобрать максимальное соотношение 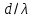 , поскольку исходя из условий, менять значения , поскольку исходя из условий, менять значения 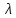 невозможно, необходимо подобрать такое максимальное невозможно, необходимо подобрать такое максимальное 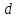 , при котором выполнялось бы условие задания. , при котором выполнялось бы условие задания.Максимальное значения 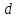 , при котором выполняется условие задания, был найдено методом подбора, и равно , при котором выполняется условие задания, был найдено методом подбора, и равно 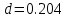 м. На рисунке 2 изображена диаграмма направленности при заданном значении расстояния между элементами. м. На рисунке 2 изображена диаграмма направленности при заданном значении расстояния между элементами.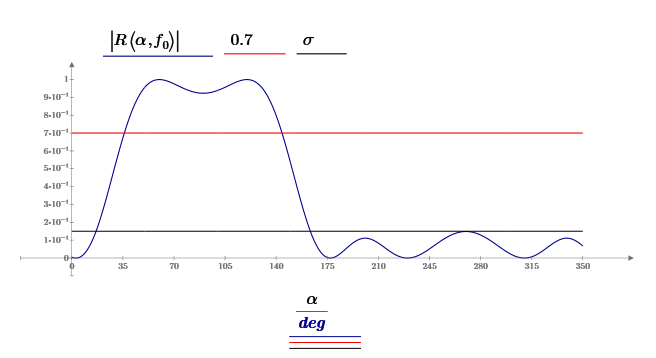 Рисунок 2 - Диаграмма направленности при заданном значении расстояния между элементами. Направленные свойства АР на разных частотахНа рисунках 3-6 представлены диаграммы направленности АР при разных значениях рабочей частоты, при постоянном расстоянии между элементами 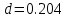 м. м.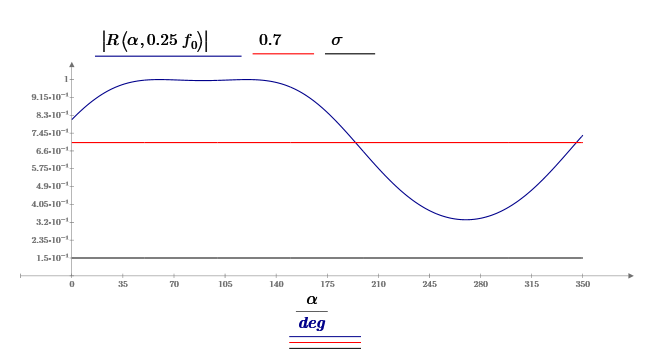 Рисунок 3 - Диаграмма направленности АР на частоте 0,25f0 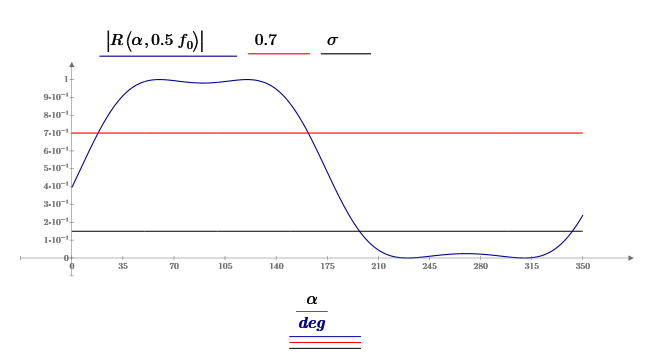 Рисунок 4 - Диаграмма направленности АР на частоте 0,5f0  Рисунок 5 - Диаграмма направленности АР на частоте f0 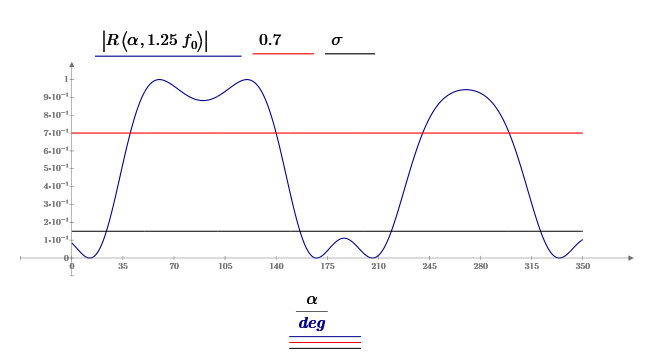 Рисунок 6 - Диаграмма направленности АР на частоте 1,25f0 При изменении рабочей частоты, изменяется отношение 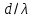 , что приводит к уменьшению боковых максимумов и увеличению площади главного максимума при уменьшении рабочей частоты, и противоположным изменениям при увеличении частоты. Так же видно, что эти изменения не линейны, так как при небольшом уменьшении площади главного лепестка, на частотах , что приводит к уменьшению боковых максимумов и увеличению площади главного максимума при уменьшении рабочей частоты, и противоположным изменениям при увеличении частоты. Так же видно, что эти изменения не линейны, так как при небольшом уменьшении площади главного лепестка, на частотах 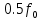 и и 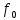 , наблюдается «небольшое» увеличение бокового максимума, но на частотах , наблюдается «небольшое» увеличение бокового максимума, но на частотах 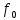 и и 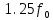 наблюдается резкий «скачёк» боковых максимумов. наблюдается резкий «скачёк» боковых максимумов.Одной из важных характеристик АР является ей коэффициент концентрации (КК). Коэффициент концентрации линейной эквидистантной антенной решетки с разными амплитудами колебания элементов: 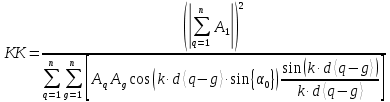 ,(4) ,(4)где n – число элементов, Aq, Ag – амплитуды колебаний элементов с номером q и g, k – волновое число, d – расстояние между элементами Формула (4) используется для расчёта коэффициента концентрации АР. На рисунке 7 представлен график зависимости коэффициента концентрации от частоты в приделах от 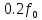 до до 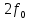 . .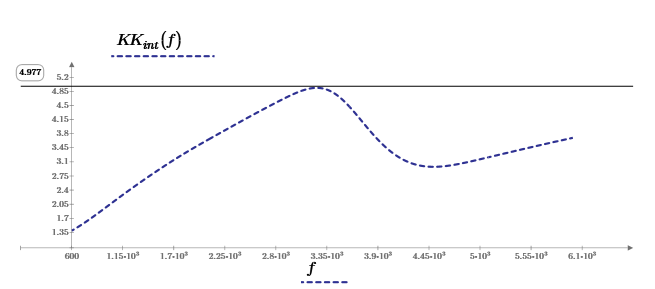 Рисунок 7 - График зависимости коэффициента концентрации от частоты Сравнение направленных свойств заданной дискретной базы и сплошной полосы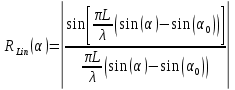 ,(5) ,(5)где L – длинна сплошной полосы. Сравнение диаграмм направленности АР и сплошной полосы длиной равной АР, на частоте 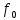 и и 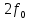 , представлено на рисунках 8 9. , представлено на рисунках 8 9.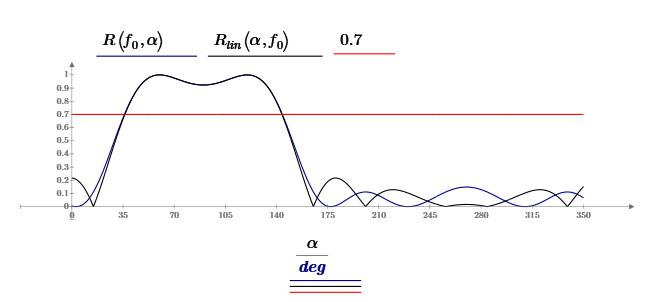 Рисунок 8 – Диаграмма направленности дискретной антенной решётки и сплошной полосы на частоте f0 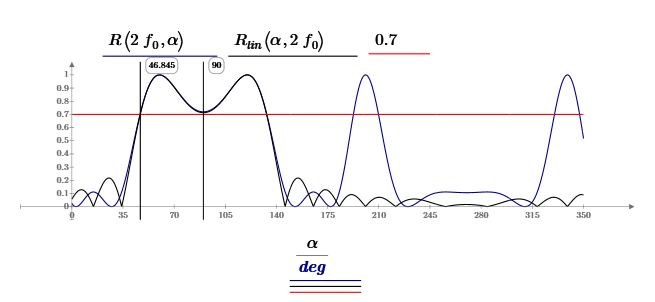 Рисунок 9 – Диаграмма направленности дискретной антенной решётки и сплошной полосы на частоте 2*f0 На рисунках 9 видно, что сплошная полоса и дискретная решётка обладают одинаковой ширеной главного лепестка равной 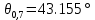 . .Коэффициент концентрации сплошной полосы: 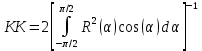 ,(6) ,(6)В таблице 2 представлены значения коэффициента концентрации АР и сплошной полосы на частотах 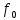 и и 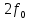 . .Таблица 2 – Значения коэффициента концентрации
На частоте f0 сплошная полоса и дискретная АР обладают одинаковым КК, при увеличении частоты в два раза, КК дискретной антенной решётки в два раза меньше КК сплошной полосы. ЗаключениеВ курсовой работе были произведены расчеты характеристик направленности эквидистантной акустической антенной решетки из пяти элементов, с неравномерным амплитудным распределением. Данная работа показала влияние соотношения 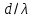 на направленность антенной решётки. на направленность антенной решётки. Также проведено сравнение направленных свойств заданной антенной решетки и сплошной полосы, длина которой равна длине антенной решетки. Список литературы1. Г.М. Свердлин Прикладная гидроакустика: Учебное пособие. – 2 изд., перераб. и доп. –Л.: Судостроение, 1990. – 320с., ил. 2. Евтютов А.П., Митько В.Б. Инженерные расчёты в гидроакустике – 2 изд., перераб. и доп. –Л.: Судостроение, 1988. – 288с., ил. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
