Инженерный бизнес и менеджмент

Название	Инженерный бизнес и менеджмент
Дата	02.10.2022
Размер	255.8 Kb.
Формат файла
Имя файла	DZ_Ekonometrika1.docx
Тип	Учебный комплекс #709275
страница	1 из 2

1 2

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский государственный технический университет имени Н.Э.Баумана

(национальный исследовательский университет)»

(МГТУ им. Н.Э.Баумана)

НАУЧНО-УЧЕБНЫЙ КОМПЛЕКС
”ИНЖЕНЕРНЫЙ БИЗНЕС И МЕНЕДЖМЕНТ”
Кафедра «Экономика и организация производства»

(ИБМ-2)
ДОМАШНЕЕ ЗАДАНИЕ №1
По дисциплине

«Эконометрика»
Тема: «Функция спроса и метод наименьших квадратов»
Вариант № 1
(Компьютерные мыши)

Студент _______________________ Зингалев Г.Е.

(Подпись) (ФИО студента)
Группа ИБМ6-43Б

Преподаватель ________________ Куликова С.Ю.

(Подпись) (ФИО преподавателя)

Москва

2022г.
Цель и задачи данной работы

Цель данной работы: определить оптимальные цены, которые готовы заплатить потребители за 1 компьютерную мышь, на основе результатов опроса 50 респондентов о максимальной цене.

Задачи данной работы:

Провести опрос 50-ти человек и узнать, какую максимальную цену они готовы заплатить за 1 компьютерную мышь.
Найти значение функции спроса.
Построить на графике выборочную функцию спроса.
Восстановить функцию спроса методом наименьших квадратов, используя линейную аппроксимизацию.
Рассчитать доверительные границы.
Сопоставить результаты оптимизации на основе выборочной функции спроса.
Сделать вывод.

Часть 1.
Построение выборочной функции спроса и расчет оптимальной цены.

Составить выборку из 50 человек.
Провести опрос и узнать, какую максимальную цену готовы заплатить за компьютерную мышь респонденты.
Полученные при опросе цены, руб.: 2000, 1500, 1500, 3500, 3000, 3500, 2000, 2500, 1000, 1500, 4000, 2000, 1800, 3200, 3400, 1500, 2000, 4000, 3500, 4000, 1500, 2000, 3500, 1000, 5000, 1500, 800, 1700, 1600, 2000, 2100, 3000, 2800, 4900, 1400, 4500, 3700, 1400, 1700, 4300, 1200, 2000, 1600, 4000, 2700, 1500, 1800, 2800, 2800, 3700, 3200.
Расположить цены по возрастанию, заполнить таблицу и оценить функцию спроса.

Tаблица 1 - Эмпирическая оценка функции спроса

№ п/п	Цена руб.	N повторов	D (p)
1	800	1	50
2	1000	2	49
3	1200	1	47
4	1400	2	46
5	1500	6	44
6	1600	2	38
7	1700	2	36
8	1800	2	34
9	2000	7	32
10	2100	1	25
11	2500	2	24
12	2700	1	22
13	2800	3	21
14	3000	1	18
15	3200	2	17
16	3400	1	15
17	3500	3	14
18	3700	2	11
19	4000	4	9
20	4300	1	5
21	4500	1	4
22	4900	1	3
23	5000	2	2

Пояснения к таблице:

№ - номера значений цен;

Цена, руб (Pᵢ) – цены, которые назвали респонденты в порядке возрастания и без повторений (Pᵢ);

Повторы N(i) - количество повторных цен (Nᵢ);

Спрос D(pᵢ) – Спрос на данный товар при определённой цене Pᵢ.

Вывод: 50 респондентов назвали 23 цены за компьютерную мышь.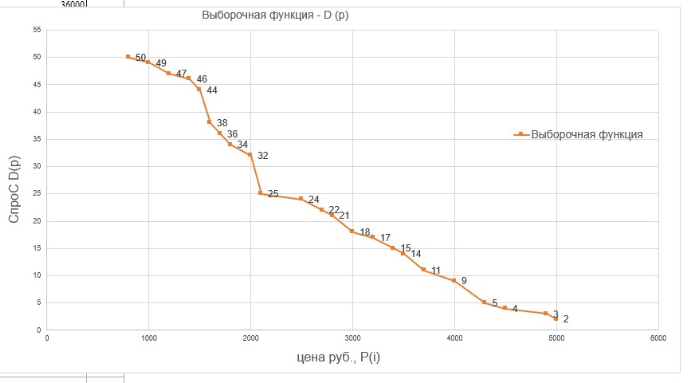

Рисунок 1 - Функция спроса

Проанализировав функцию спроса, можно увидеть, что чем дороже стоит принтер, тем меньше на него спрос.
Расчёт оптимальных цен

Нахождение значения максимальной прибыли для значения издержек.

П = (𝑃_𝑖 − 𝑃₀) ∗ 𝐷(𝑃_𝑖) → 𝑚𝑎𝑥, где

^P0 ^{– издержки производителя или оптовая цена, руб.;}

^Pi ^–^{розничная}^{цена, руб.};

^D(^pi⁾^{– спрос}^{от цены;}

Зададим значение издержек и рассчитаем оптимальные цены при:

P₀₁= 100 руб.;

P₀₂= 300 руб.;

P₀₃= 500 руб.;

P₀₄= 700 руб.;

P₀₅= 1000 руб.
Таблица 2 - Расчет оптимальной цены

№ п/п	Цена руб.	N повторов	D (p)	*Прибыль, (Pi - 100) D(Pi)**	*Прибыль, (Pi - 300) D(Pi)**	*Прибыль, (Pi - 500) D(Pi)**	*Прибыль, (Pi - 700) D(Pi)**	*Прибыль, (Pi - 1000) D(Pi)**
1	800	1	50	35000	25000	15000	5000	-10000
2	1000	2	49	44100	34300	24500	14700	0
3	1200	1	47	51700	42300	32900	23500	9400
4	1400	2	46	59800	50600	41400	32200	18400
5	1500	6	44	61600	52800	44000	35200	22000
6	1600	2	38	57000	49400	41800	34200	22800
7	1700	2	36	57600	50400	43200	36000	25200
8	1800	2	34	57800	51000	44200	37400	27200
9	2000	7	32	60800	54400	48000	41600	32000
10	2100	1	25	50000	45000	40000	35000	27500
11	2500	2	24	57600	52800	48000	43200	36000
12	2700	1	22	57200	52800	48400	44000	37400
13	2800	3	21	56700	52500	48300	44100	37800
14	3000	1	18	52200	48600	45000	41400	36000
15	3200	2	17	52700	49300	45900	42500	37400
16	3400	1	15	49500	46500	43500	40500	36000
17	3500	3	14	47600	44800	42000	39200	35000
18	3700	2	11	39600	37400	35200	33000	29700
19	4000	4	9	35100	33300	31500	29700	27000
20	4300	1	5	21000	20000	19000	18000	16500
21	4500	1	4	17600	16800	16000	15200	14000
22	4900	1	3	14400	13800	13200	12600	11700
23	5000	2	2	9800	9400	9000	8600	8000

Пример расчета для случайно выбранных цен:

Прибыль, (Pi - 100) * D(Pi)

(800 – 100) * 50 = 35000 руб. (При цене 800 рублей)

Прибыль, (Pi - 300) * D(Pi)

(800-300) * 50 = 25000руб. (При цене 800 рублей)

Прибыль, (Pi - 500) * D(Pi)

(2000-500) * 32 = 48000 руб. (При цене 2000 рублей)

Прибыль, (Pi - 700) * D(Pi)

(2800-700) * 21= 44100 руб. (При цене 2800 рублей)

Прибыль, (Pi – 1000) * D(Pi)

(4500-1000) * 4= 14000 руб. (При цене 4500 рублей)

Проанализировав таблицу 2, можно сделать вывод, что при первых двух значениях, которые имеют небольшую величину издержек максимальная прибыль достигается в одной цене, а при повышении себестоимости товара максимальная прибыль уменьшается и цена становится намного больше:

При P₀₁= 100 рублей максимальная прибыль равна 61600 рублей;

При P₀₂= 300 рублей максимальная прибыль равна 54400 рублей;

При P₀₃= 500 рублей максимальная прибыль равна 48400 рублей;

При P₀₄= 700 рублей максимальная прибыль равна 44100 рублей;

При P₀₅= 1000 рублей максимальная прибыль равна 37800 рублей.

Таблица 3 - Оптимальные цены при издержках производителя

Р (издержки), в руб.	Р(оптимальная), в руб
100	1500
300	2000
500	2700
700	2800
1000	2800

Проанализировав таблицу 3, можно сделать вывод, если оптовая цена или издержки повышаются, вероятно, повысится и розничная цена. Повышение издержек приводит к снижению прибыли и уменьшению доли покупателей, готовых приобрести товар.

100 рублей  1500 рублей  44 человек (88%);

300 рублей  2000 рублей  32 человек (64%);

500 рублей  2700 рублей  22 человека (44%);

700 рублей  2800 рублей  21 человек (42%);

1000 рублей  2800 рублей  21 человек (42%).

1 2