Институт непрерывного и дистанционного образования кафедра вычислительных систем и программирования

Название	Институт непрерывного и дистанционного образования кафедра вычислительных систем и программирования
Анкор	lab 2 matlab
Дата	21.09.2022
Размер	0.79 Mb.
Формат файла
Имя файла	laba2_Matlab.docx
Тип	Отчет #688120

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ И ПРОГРАММИРОВАНИЯ

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

доцент, к.т.н.				В.А. Ненашев
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ

по дисциплине: МОДЕЛИРОВАНИЕ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №
	номер группы		подпись, дата		инициалы, фамилия

Санкт-Петербург

2021

Цель работы:

ознакомление с возможностями MATLAB по изучению основных законов распределений одномерных случайных величин;
исследование зависимости графиков функций распределения и функций плотности вероятности от параметров распределений;
моделирование и анализ одномерных случайных величин в MATLAB.

Номер варианта: 10.

Для каждого вида распределений (нормальный, равномерный, экспоненциальный и Рэлея) написать программу вывода в графическом окне графиков функций распределения с использованием функций MATLAB.

Графики плотности и функции распределения для нормального закона распределения

На рисунке 1 изображен график плотности распределения по нормальному закону.

Рисунок 1 - График плотности распределения нормального закона

На рисунке 2 изображен график функции распределения нормального закона.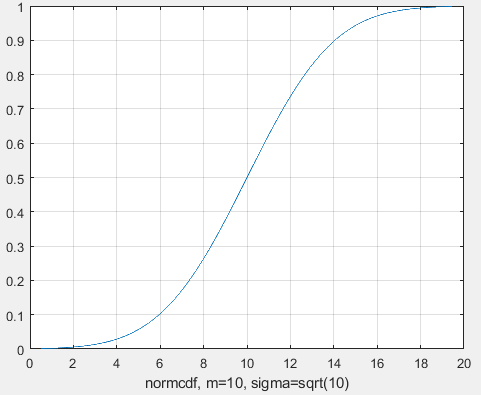

Рисунок 2 - График функции распределения нормального закона

Листинг программы:

clear all

m=10;

sigma = sqrt(m);

x = m-3*sigma:0.01:m+3*sigma;

y_p = normpdf(x,m,sigma);

figure (1)

plot(x,y_p)

grid on

xlabel('normpdf, m=10, sigma=sqrt(10)')

axis([0 20 0 0.14]);

y_F = normcdf(x,m,sigma);

figure (2)

plot(x,y_F)

grid on

xlabel('normcdf, m=10, sigma=sqrt(10)')

axis([0 20 0 1]);

Графики плотности и функции для равномерного закона распределения

На рисунке 3 изображен график плотности распределения равномерного закона.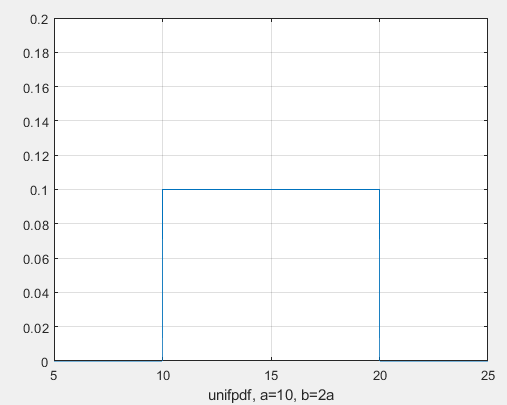

Рисунок 3 - График плотности распределения равномерного закона

На рисунке 4 изображен график функции распределения равномерного закона.

Рисунок 4 - График функции распределения равномерного закона

Листинг программы:

clear all

a=10;

b=2*a;

x = a-5:0.01:2*a+5;

y_p = unifpdf(x,a,b);

figure (1)

plot(x,y_p)

grid on

xlabel('unifpdf, a=10, b=2a')

axis([5 25 0 0.2]);

y_F = unifcdf(x,a,b);

figure (2)

plot(x,y_F)

grid on

xlabel('unifcdf, a=10, b=2a')

axis([5 25 0 1.1]);

Графики для плотности и функции распределения для экспоненциального закона распределения

На рисунке 5 изображен график плотности распределения экспоненциального закона.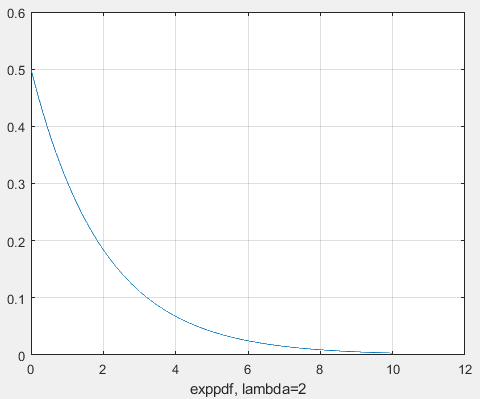

Рисунок 5 - График плотности распределения экспоненциального закона

На рисунке 6 изображен график функции распределения экспоненциального закона.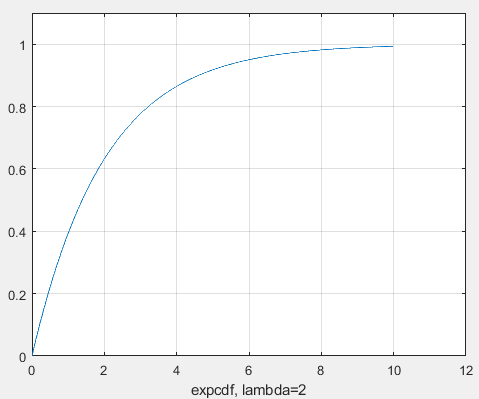

Рисунок 6 – График функции распределения экспоненциального закона

Листинг программы:

clear all

a=10;

b=2*a;

lambda=2;

x = 0:0.01:10;

y_p = exppdf(x,lambda);

figure (1)

plot(x,y_p)

grid on

xlabel('exppdf, lambda=2')

axis([0 12 0 0.6]);

y_F = expcdf(x,lambda);

figure (2)

plot(x,y_F)

grid on

xlabel('expcdf, lambda=2')

axis([0 12 0 1.1]);

Графики для плотности и функции распределения для закона распределения Рэлея

На рисунке 7 изображен график плотности распределения закона Рэлея.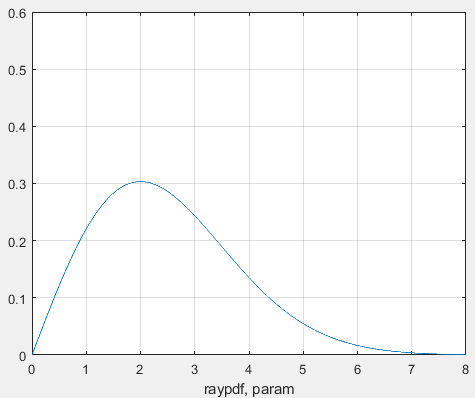

Рисунок 7 - График плотности распределения закона Рэлея

На рисунке 8 изображен график функции распределения закона Рэлея.

Рисунок 8 - График функции распределения закона Рэлея

Листинг программы:

clear all

a=10;

b=2*a;

param=2;

x = 0:0.01:10;

y_p = raylpdf(x,param);

figure (1)

plot(x,y_p)

grid on

xlabel('raypdf, param')

axis([0 8 0 0.6]);

y_F = raylcdf(x,param);

figure (2)

plot(x,y_F)

grid on

xlabel('raycdf, param')

axis([0 12 0 1.1]);

Получить реализацию случайных чисел с помощью встроенных функций MATLAB и с помощью формул для каждого закона распределения, а также построить гистограммы для N=100, 1000 и 10000

Нормальный закон распределения.

Листинг программы для реализации случайных величин (СВ) с помощью встроенной функции MATLAB:

clear all

m=10;

sigma = sqrt(m);

N=1000;

c=2*pi;

%ПО ВСТРОЕННОЙ ФУНКЦИИ

Y_vstr = normrnd(m, sigma, N, 1);

figure(1)

plot(Y_vstr)

xlabel('Номер элемента в выборке')

ylabel('Значения СВ')

grid on

figure(2)

hist(Y_vstr)

grid on

xlabel("Значение");

ylabel("Частота");

axis([0 20 0 300]);

Результаты работы программы: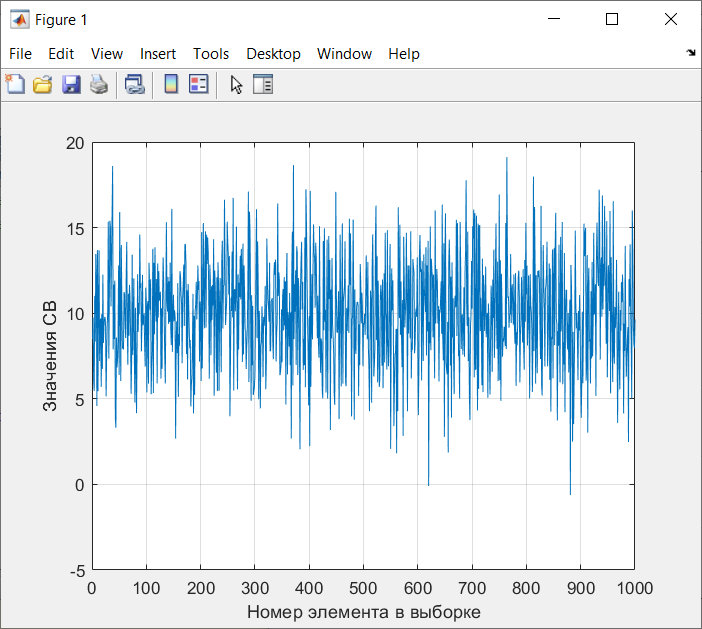

Рисунок 9 - График распределения СВ, построенный по встроенной функции MATLAB, при N=1000

Листинг программы для реализации СВ с помощью формулы:

%ПО ФОРМУЛЕ

a1=rand(1,N); % сгенерировать a1 размерностью N

a2=rand(1,N); % сгенерировать a2 размерностью N

r=sqrt(-2*log(a1));

f=a2*c;

X1=r.*sin(f);

Y_form=m+sigma*X1;

figure(3)

plot(Y_form)

xlabel('Номер элемента в выборке')

ylabel('Значения СВ')

grid on

Результаты работы программы: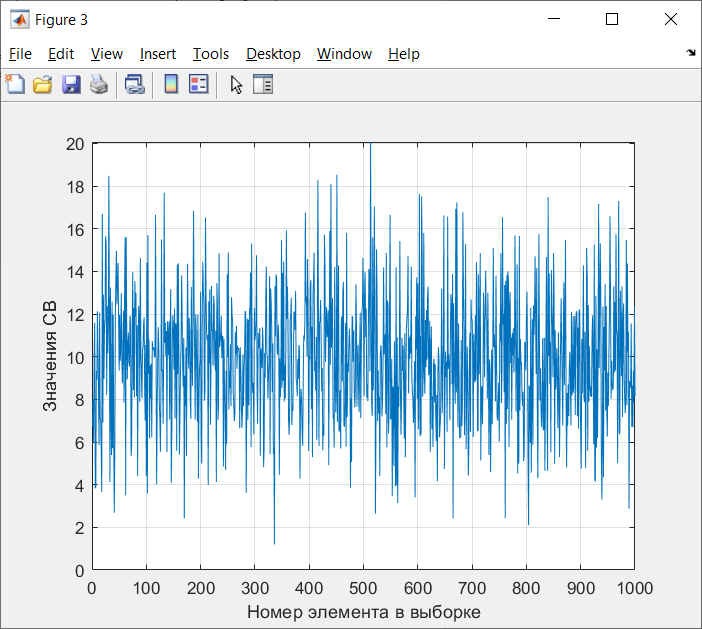

Рисунок 10 - График распределения СВ, построенный с помощью формулы, при N=1000

Анализ и сравнение результатов и построение гистограмм, при N=100, 1000 и 10000

figure(4)

histfit(Y_form, 50)

grid on

xlabel("Значение");

ylabel("Вероятность");

axis([0 60 0 300]);

m_y = mean (Y_form) % вычисление мат. ожидания

st_y = std (Y_form) % вычисление СКО

sk_Y = skewness(Y_form) % вычисление коэффициента асимметрии

kur_Y = kurtosis(Y_form)-3 % вычисление коэффициента эксцесса

Результаты работы программы: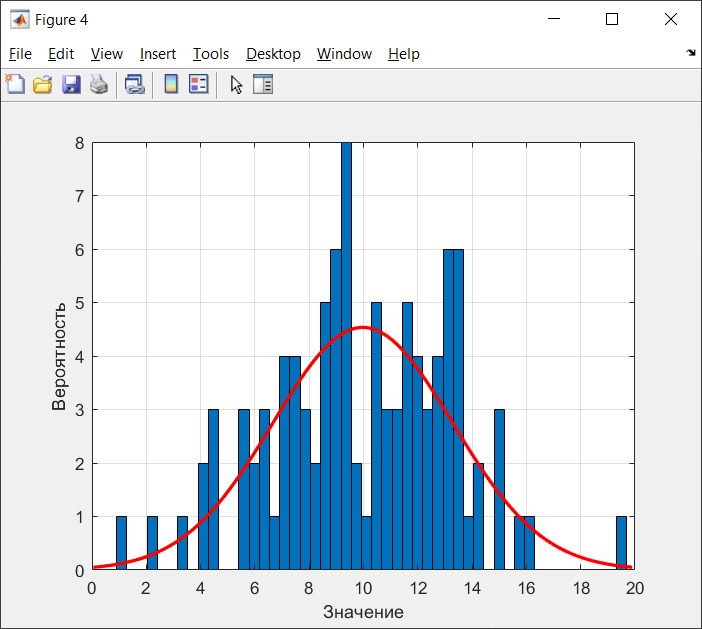

Рисунок 11 - Гистограмма нормального распределения СВ, при N=100

Вычисленные значения, при N=100:

Математическое ожидание: 9.9745

Дисперсия: 10.9379

СКО: 3.3072

Коэффициент асимметрии: -0.1216

Коэффициент эксцесса: 0.0342

Рисунок 12 - Гистограмма нормального распределения СВ, при N=1000

Вычисленные значения, при N=1000:

Математическое ожидание: 10.0572

Дисперсия: 9.3376

СКО: 3.0558

Коэффициент асимметрии: 0.0943

Коэффициент эксцесса: -0.2663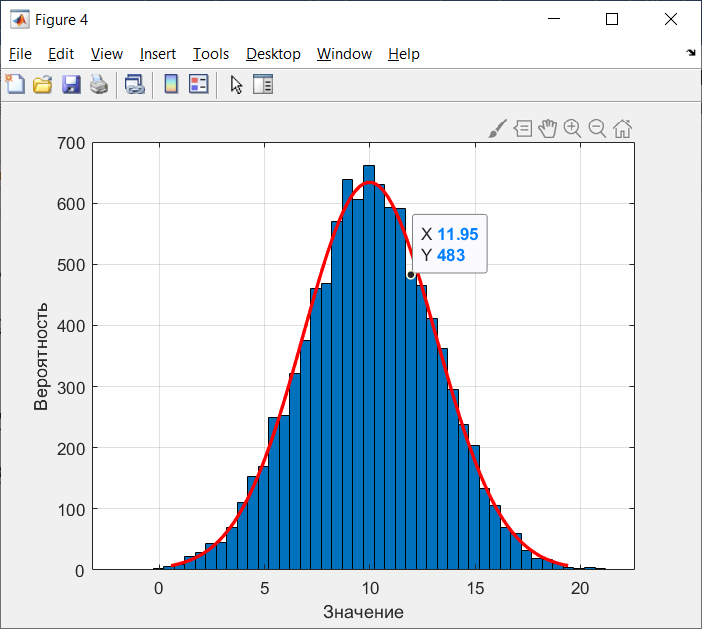

Рисунок 13 - Гистограмма нормального распределения СВ, при N=10000

Вычисленные значения, при N=10000:

Математическое ожидание: 9.9836

Дисперсия: 9.8925

СКО: 3.1452

Коэффициент асимметрии: -0.0346

Коэффициент эксцесса: -0.0346

Равномерный закон распределения.

Листинг программы для реализации СВ с помощью встроенной функции матлаб:

clear all

a=10;

b=2*a;

N=1000;

c=2*pi;

%ПО ВСТРОЕННОЙ ФУНКЦИИ

Y_vstr = unifrnd(a, b, N, 1);

figure(1)

plot(Y_vstr)

xlabel('Номер элемента в выборке')

ylabel('Значения СВ')

grid on

Результаты работы программы: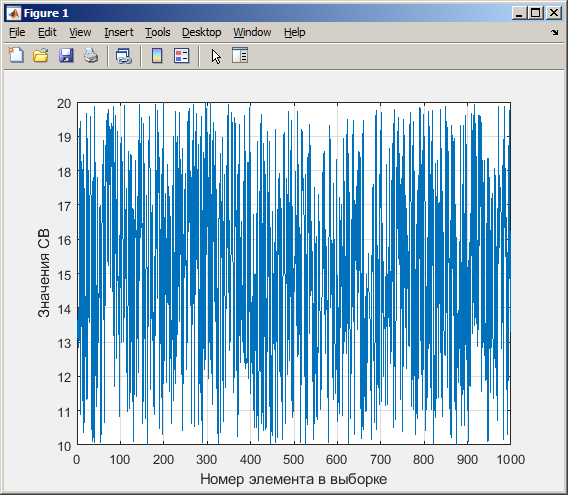

Рисунок 14 - График распределения СВ, построенный по встроенной функции MATLAB, при N=1000

Листинг программы для реализации СВ с помощью формулы:

%ПО ФОРМУЛЕ

a1=rand(1,N); % сгенерировать a1 размерностью N

Y_form=a+(b-a)*a1;

figure(2)

plot(Y_form)

xlabel('Номер элемента в выборке')

ylabel('Значения СВ')

grid on

Результаты работы программы: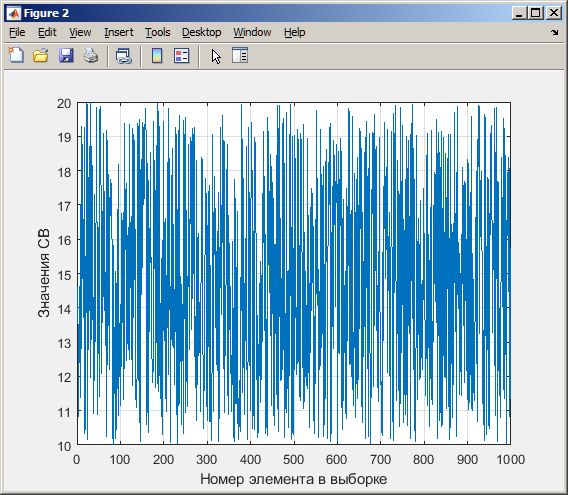

Рисунок 15 - График распределения СВ, построенный с помощью формулы, при N=1000

Анализ и сравнение результатов и построение гистограмм, при N=100, 1000 и 10000

figure(4)

histfit(Y_form, 50)

grid on

xlabel("Значение");

ylabel("Вероятность");

axis([0 60 0 300]);

m_y = mean (Y_form) % вычисление мат. ожидания

st_y = std (Y_form) % вычисление СКО

sk_Y = skewness(Y_form) % вычисление коэффициента асимметрии

kur_Y = kurtosis(Y_form)-3 % вычисление коэффициента эксцесса

Результаты работы программы: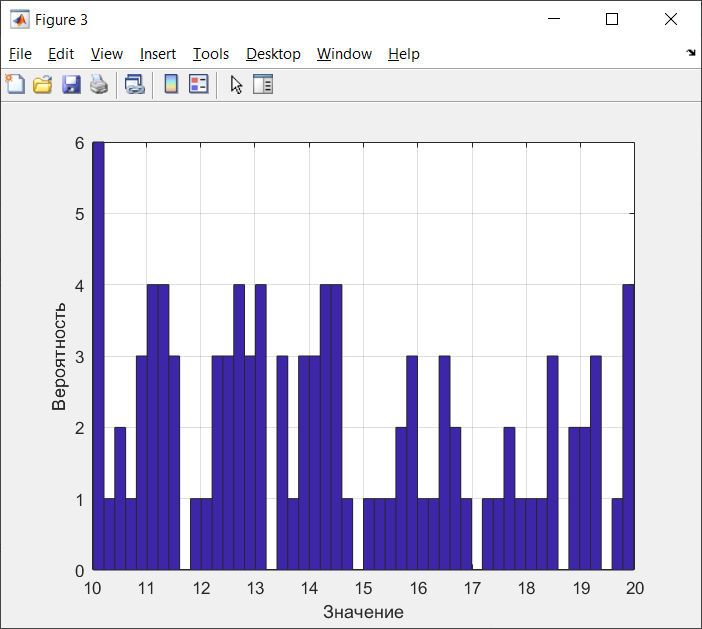

Рисунок 16 - Гистограмма равномерного распределения СВ, при N=100

Вычисленные значения, при N=100:

Математическое ожидание: 14.3728

Дисперсия: 8.7093

Коэффициент асимметрии: 0.3433

Коэффициент эксцесса: -1.0264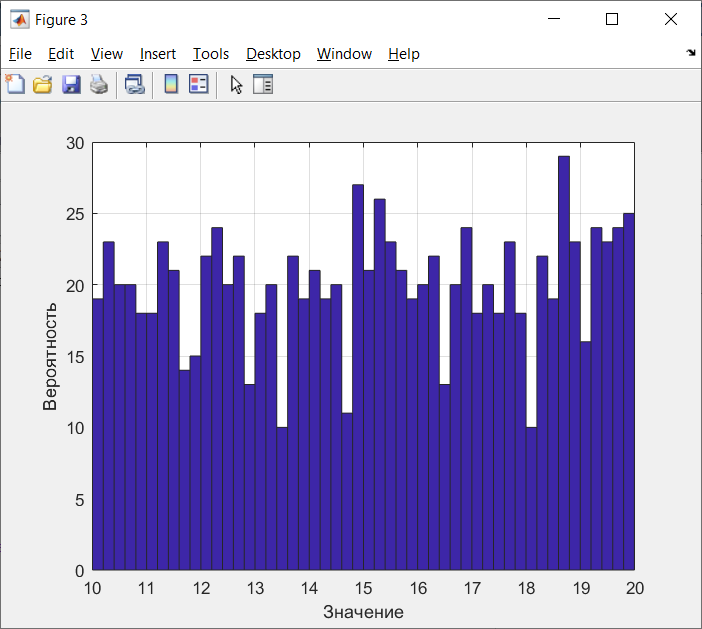

Рисунок 17 - Гистограмма равномерного распределения СВ, при N=1000

Вычисленные значения, при N=1000:

Математическое ожидание: 15.1116

Дисперсия: 8.5515

Коэффициент асимметрии: -0.0418

Коэффициент эксцесса: -1.2041

Рисунок 18 - Гистограмма равномерного распределения СВ, при N=10000

Вычисленные значения, при N=10000:

Математическое ожидание: 14.9784

Дисперсия: 8.3401

Коэффициент асимметрии: 0.0150

Коэффициент эксцесса: -1.2070

Экспоненциальный закон распределения.

Листинг программы для реализации СВ с помощью встроенной функции матлаб:

clear all

lambda=2;

m=1/lambda;

N=1000;

%ПО ВСТРОЕННОЙ ФУНКЦИИ

Y_vstr = exprnd(m, N, 1);

figure(1)

plot(Y_vstr)

xlabel('Номер элемента в выборке')

ylabel('Значения СВ')

grid on

Результаты работы программы: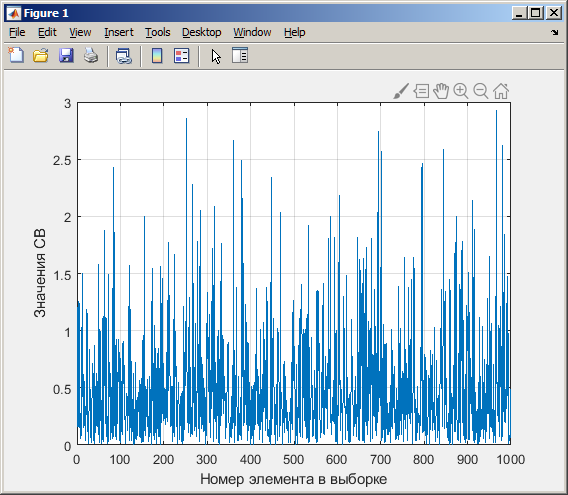

Рисунок 112 - График распределения СВ, построенный по встроенной функции MATLAB, при N=1000

Листинг программы для реализации СВ с помощью формулы:

%ПО ФОРМУЛЕ

a1=rand(1,N); % сгенерировать a1 размерностью N

Y_form=log(a1)/(-lambda);

figure(2)

plot(Y_form)

xlabel('Номер элемента в выборке')

ylabel('Значения СВ')

grid on

Результаты работы программы: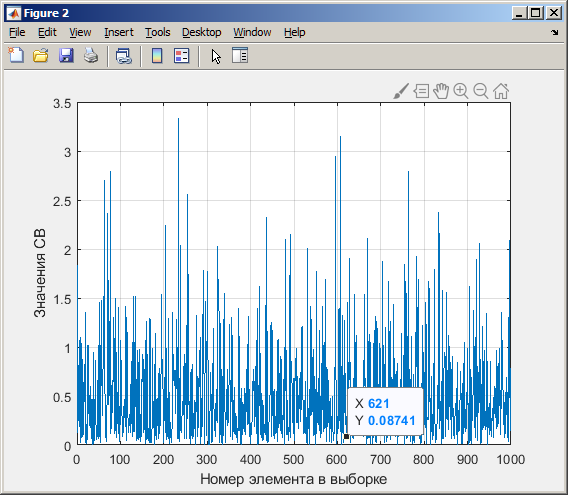

Рисунок 13 - График распределения СВ, построенный с помощью формулы, при N=1000

Анализ и сравнение результатов и построение гистограмм, при N=100, 1000 и 10000

figure(4)

histfit(Y_form, 50, 'exponential')

grid on

xlabel("Значение");

ylabel("Вероятность");

m_y = mean (Y_form) % вычисление мат. ожидания

st_y = std (Y_form) % вычисление СКО

sk_Y = skewness(Y_form) % вычисление коэффициента асимметрии

kur_Y = kurtosis(Y_form)-3 % вычисление коэффициента эксцесса

Результаты работы программы: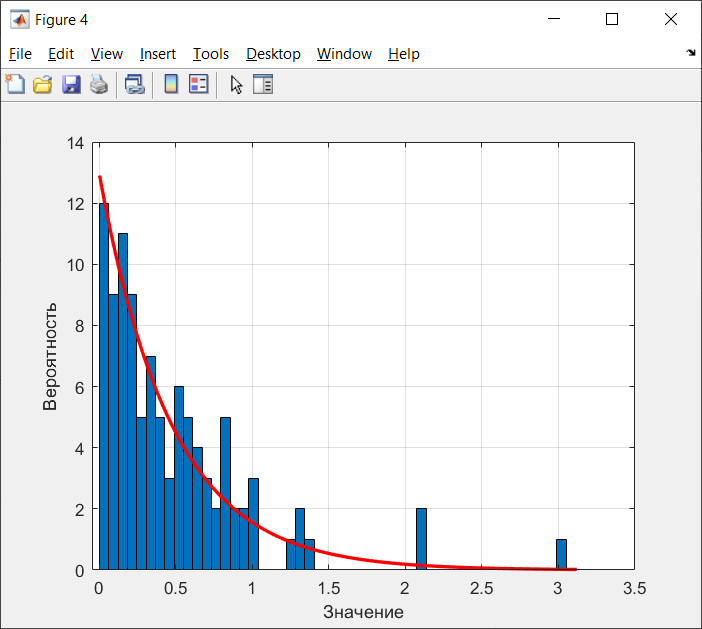

Рисунок 14 - Гистограмма экспоненциального распределения СВ, при N=100

Вычисленные значения, при N=100:

Математическое ожидание: 0.4721

Дисперсия: 0.2330

СКО: 0.4827

Коэффициент асимметрии: 2.3511

Коэффициент эксцесса: 7.9122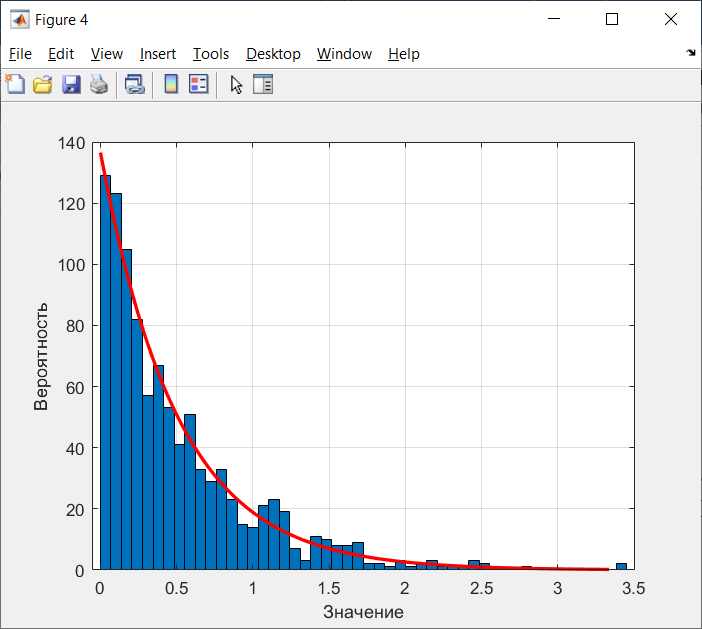

Рисунок 22 - Гистограмма экспоненциального распределения СВ, при N=1000

Вычисленные значения, при N=1000:

Математическое ожидание: 0.5046

Дисперсия: 0.2509

СКО: 0.5009

Коэффициент асимметрии: 1.7808

Коэффициент эксцесса: 4.1622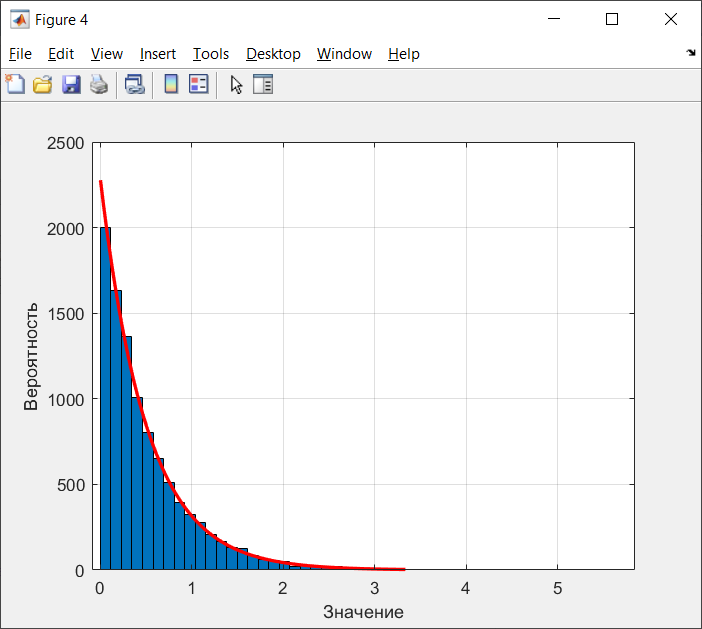

Рисунок 23 - Гистограмма экспоненциального распределения СВ, при N=10000

Вычисленные значения, при N=10000:

Математическое ожидание: 0.5044

Дисперсия: 0.2524

СКО: 0.5024

Коэффициент асимметрии: 1.9781

Коэффициент эксцесса: 5.9436

Рэлеязакон распределения.

Листинг программы для реализации СВ с помощью встроенной функции матлаб:

clear all

m=10;

sigma = sqrt(m);

N=1000;

%ПО ВСТРОЕННОЙ ФУНКЦИИ

Y_vstr = raylrnd(sigma, N, 1);

figure(1)

plot(Y_vstr)

xlabel('Номер элемента в выборке')

ylabel('Значения СВ')

grid on

figure(2)

hist(Y_vstr)

grid on

xlabel("Значение");

ylabel("Частота");

axis([0 20 0 300]);

Результаты работы программы: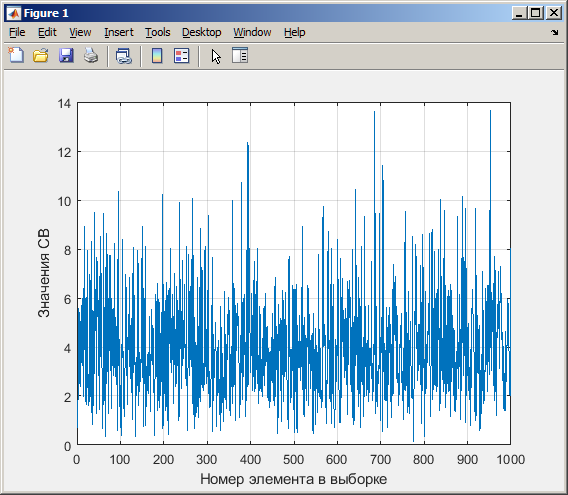

Рисунок 24 - График распределения СВ, построенный по встроенной функции MATLAB, при N=1000

Листинг программы для реализации СВ с помощью формулы:

%ПО ФОРМУЛЕ

a1=rand(1,N); % сгенерировать a1 размерностью N

Y_form=sigma*sqrt(-2*log(a1));

figure(3)

plot(Y_form)

xlabel('Номер элемента в выборке')

ylabel('Значения СВ')

grid on

Результаты работы программы: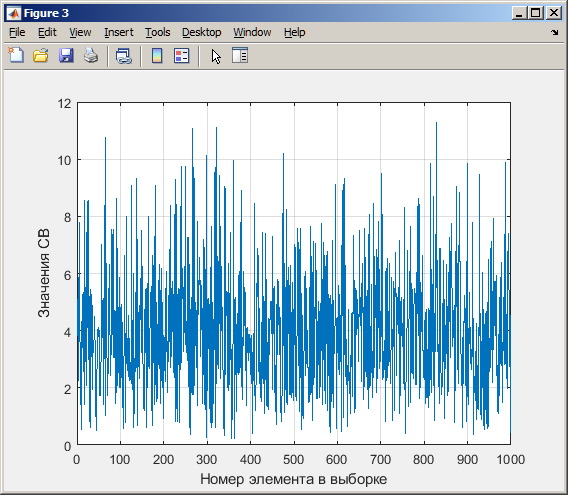

Рисунок 25 - График распределения СВ, построенный с помощью формулы, при N=1000

Анализ и сравнение результатов и построение гистограмм, при N=100, 1000 и 10000

figure(4)

histfit(Y_form, 50, 'rayleigh')

grid on

xlabel("Значение");

ylabel("Вероятность");

m_y = mean (Y_form) % вычисление мат. ожидания

d_y = var(Y_form) % вычисление дисперсии

st_y = std (Y_form) % вычисление СКО

sk_Y = skewness(Y_form) % вычисление коэффициента асимметрии

kur_Y = kurtosis(Y_form)-3 % вычисление коэффициента эксцесса

Результаты работы программы: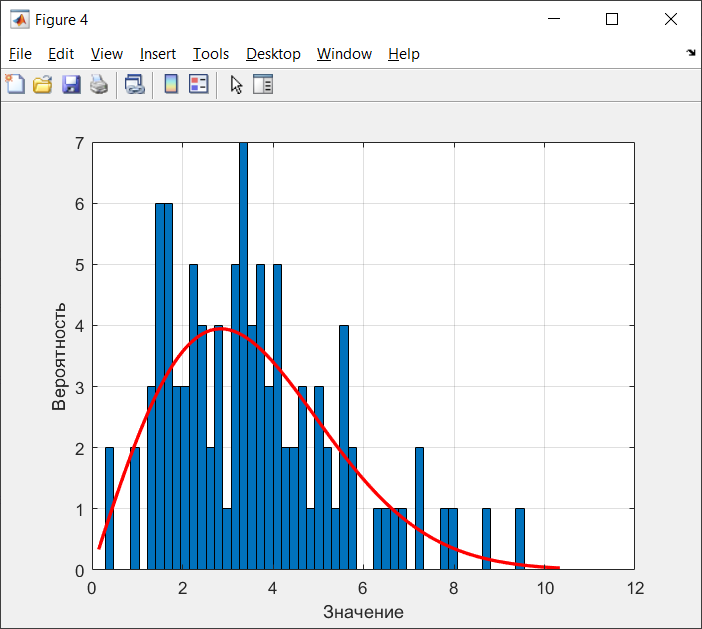

Рисунок 26 - Гистограмма Рэлей распределения СВ, при N=100

Вычисленные значения, при N=100:

Математическое ожидание: 3.5661

Дисперсия: 3.4963

СКО: 1.8698

Коэффициент асимметрии: 0.8352

Коэффициент эксцесса: 0.5363

Рисунок 27 - Гистограмма Рэлей распределения СВ, при N=1000

Вычисленные значения, при N=1000:

Математическое ожидание: 4.1366

Дисперсия: 4.2540

СКО: 2.0625

Коэффициент асимметрии: 0.6203

Коэффициент эксцесса: 0.3559

Рисунок 28 - Гистограмма Рэлей распределения СВ, при N=10000

Вычисленные значения, при N=10000:

Математическое ожидание: 3.9658

Дисперсия: 4.3892

СКО: 2.0950

Коэффициент асимметрии: 0.6413

Коэффициент эксцесса: 0.2731

Теоретические значения числовых характеристик СВ

Нормальный закон

m = 10;

D = σ² = 10;

σ =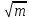

= 3.1623;

A_s = 0;

γ₂ = 0;

Равномерный закон

m =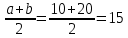

;

D =

;

A_s = 0;

γ₂ = -6/5 = -1.2;

Экспоненциальный закон

m = 1/λ = ½ = 0.5;

D = 1/λ² = ¼ = 0.25;

A_s = 2;

γ₂ = 6;

Рэлея закон

m =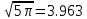

;

σ =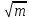

= 3.1623;

D = (2 – π/2) * σ² = 20 - 5π = 4.3;

A_s = 0.631;

γ₂ = 0.245;

Таблица сравнения теоретических числовых характеристик СВ и характеристик, полученных по моделируемой выборке

Таблица 1 – Сравнение теоретических характеристик СВ с характеристиками СВ полученных эмпирически

Характеристика Распределение	M[X]		D[X]		Ex[X]			Sk[X]
Характеристика Распределение	теор.	выбор. N=100, 1000, 10000	теор.	выбор. N=100, 1000, 10000	теор.	выбор. N=100, 1000, 10000	теор.		выбор. N=100, 1000, 10000
Нормальное N(m, σ)	10	9.9745, 10.0572, 9.9836	10	10.9379, 9.3376, 9.8925	0	-0.1216, 0.0943, -0.0346	0		0.0342, -0.2663, -0.0346
Равномерное R(a, b)	15	14.3728, 15.1116, 14.9784	8.333	8.7093, 8.5515, 8.3401	0	0.3433, -0.0418, 0.0150	-1.2		-1.0264, -1.2041, -1.2070
Экспоненциальное E(λ)	0.5	0.4721, 0.5046, 0.5044	0.25	0.2330, 0.2509, 0.2524	2	2.3511, 1.7808, 1.9781	6		7.9122, 4.1622, 5.9436
Рэлея	3.963	3.5661, 4.1366, 3.9658	4.3	3.4963, 4.2540, 4.3892	0.631	0.8352, 0.6203, 0.6413	0.245		0.5363, 0.3559, 0.2731

Выводы:

В ходе выполнения лабораторной работы были написаны программы вывода в графическом окне графиков функций распределения с использованием функций MATLAB.
Были получены реализации случайных величин с помощью формул для каждого закона распределения и построены гистограммы для N=100, 1000 и 10000.
Гистограммы и числовые характеристики, во всех представленных законах распределения, найденных эмпирически, с увеличением объема выборки становятся ближе к теоретическим значениям.