Кейс_задачи_ПОНИС_вар 9. Институт непрерывного образования
 Скачать 58.04 Kb. Скачать 58.04 Kb.
|
|
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ Кейс-задачи По дисциплине «Проектная оценка надежности информационных систем» Вариант 9 Фамилия: Имя: Отчество: Курс: Студ. билет №: Группа №: Дата сдачи работы: ________ Санкт-Петербург 2022 СодержаниеСАНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ 1 УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича 1 ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ 1 Кейс-задачи По дисциплине «Проектная оценка надежности информационных систем» 1 Вариант 9 1 Фамилия: 1 Имя: 1 Отчество: 1 Курс: 1 Студ. билет №: 1 Группа №: 1 Санкт-Петербург 1 Задача №1 3 Задача №2 6 Задача №3 8 Задача №4 10 Задача №1При проектировании информационной системы обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t)≥ 0,97. Исходные данные: Проектируемая система состоит из 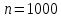 элементов. элементов.Средняя интенсивность отказов для элементов 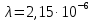 . .Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. Время работы 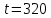 . .Определить: Вероятность безотказной работы заданной системы. Как следует изменить количество элементов системы, чтобы надежность системы удовлетворяла поставленным требованиям? Как следует изменить надежность элементов системы, чтобы надежность всей системы удовлетворяла поставленным требованиям? Как следует изменить время работы системы, чтобы надежность системы удовлетворяла поставленным требованиям? Вопрос 1. Вероятность безотказной работы невосстанавливаемой системы подчиняющейся экспоненциальному закону распределения рассчитывается по формуле: 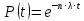 Подставив значения получим: 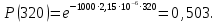 То есть вероятность безотказной работы невосстанавливаемой системы подчиняющейся экспоненциальному закону распределения в нашем случае равна 0,503, что не удовлетворяет условиям. Определим условия, при которых будет выполняться неравенство 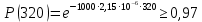 После логарифмирования обеих частей неравенства можно определить, что 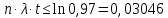 Вопрос 2. Количество элементов в системе оказывает влияние на надёжность. Увеличение количества элементов приводит к резкому ухудшению надёжности. Следовательно, для того, чтобы система удовлетворяла поставленным требованиям (P(t)≥ 0,97) количество элементов должно принимать следующие значения: 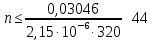 , ,Вопрос 3. На надежность элементов системы влияет интенсивность отказов. Увеличение интенсивности отказов приводит к резкому ухудшению надёжности. Следовательно, для того, чтобы система удовлетворяла поставленным требованиям (P(t)≥ 0,97) значение интенсивности отказов должно принимать следующие значения: 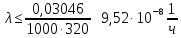 Вопрос 4. Интенсивность отказов в зависимости от времени эксплуатации имеет следующую зависимость – увеличение времени работы приводит к ухудшению надёжности. следовательно для того, чтобы система удовлетворяла поставленным требованиям (P(t)≥ 0,97) время работы должно принимать следующие значения: 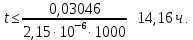 Задача №2При проектировании информационной системы обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t)≥ 0,97. Исходные данные: Проектируемая система состоит из 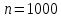 элементов. элементов.Средняя интенсивность отказов для элементов 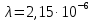 . .Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. Время работы 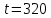 . .Определить: Кратность резервирования всей системы, обеспечивающую требуемое значение вероятности безотказной работы (P(t)). Решение: 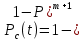 , ,Где 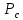 (320) = 0,97 – вероятность безотказной работы зарезервированной системы, (320) = 0,97 – вероятность безотказной работы зарезервированной системы,P(320) = 0,503 – вероятность безотказной работы исходной системы, m – искомое значение кратности резервирования системы. Решая уравнение относительно m, получим 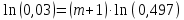 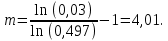 Для проверки полученного результата рассчитаем вероятность безотказной работы системы для различных вариантов резервирования. При четырёхкратном резервировании: 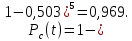 При пятикратном резервировании: 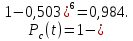 Последний результат, удовлетворяет поставленным требованиям, однако такое увеличение надежности системы стоит очень дорого. К основной системе необходимо добавить пять резервных, при этом стоимость, вес, габариты системы увеличиваются в несколько раз. Задача №3При проектировании информационной системы обеспечить надежность безотказной работы системы в длительном режиме функционирования P(t)≥ 0,97. Исходные данные: Проектируемая система состоит из 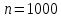 элементов. элементов.Средняя интенсивность отказов для элементов 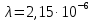 . .Вероятность безотказной работы системы подчиняется экспоненциальному закону распределения, система невосстанавливаемая. Время работы 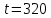 . .Определить: Кратность поэлементного резервирования системы, обеспечивающую требуемое значение вероятности безотказной работы (P(t)) 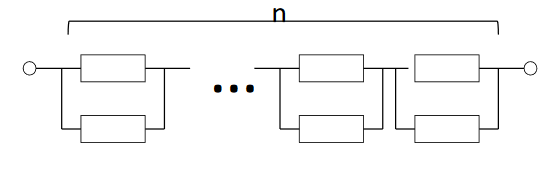 Рисунок 1. Структура системы при поэлементном резервировании системы Решение: Примем, что элементы системы равнонадежные. Из схемы, изображенной на рисунке 1, видно, что кратность резервирования элементов одинаковая. Тогда вероятность безотказной работы невосстанавливаемой системы при поэлементном резервировании системы подчиняющейся экспоненциальному закону распределения вычисляется по формуле: 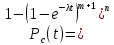 , ,где m – кратность резервирования. Сделаем расчет для кратности резервирования равной единице: 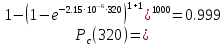 , ,Что соответствует требованиям P(t)≥ 0,97. Задача №4Исходные данные: Таблица 1 Исходные данные
Необходимо определить: 2.1 Состав нерезервируемых (nнр) и резервируемых (nр) структурных элементов системы при резервировании, части которой (nр), выполняются требования по надежности проектируемой системы. 2.2 Кратность резервирования nр-части системы 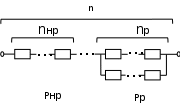 Решение: 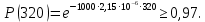 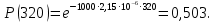 Полученное значение вероятности (0,503) безотказной работы ИС не удовлетворяет поставленным требованиям Р(320) ≥ 0,97. Количество элементов, не подлежащих резервированию 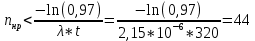 - допустимое значение элементов, не подлежащих резервированию. - допустимое значение элементов, не подлежащих резервированию.  Не резервируемая часть 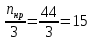 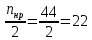 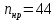 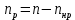   Резервируемая часть 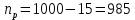 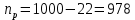 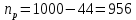 Вероятность безотказной работы нерезервируемой части системы составит: 𝑃нр=𝑒−𝑛нр𝜆𝑡 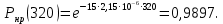 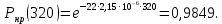 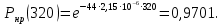 Определение требования к величине вероятности безотказной работы зарезервированной части системы 𝑃зр= 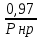 𝑃зр= 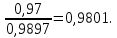 𝑃зр= 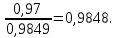 𝑃зр= 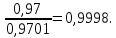 Вероятность безотказной работы резервируемой части системы до ее резервирования составляет 𝑃р=𝑒−𝑛р𝜆𝑡 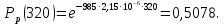 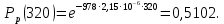 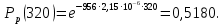 Определение кратности резервирования данной части (m) 𝑚= 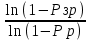 −1 −1𝑚= 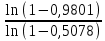 −1=4,5257 =5 −1=4,5257 =5𝑚= 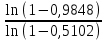 −1=4,8653=5 −1=4,8653=5𝑚= 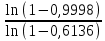 −1=7,9571=8 −1=7,9571=8Вероятность безотказной работы резервируемой части системы после ее резервирования с кратностью m=5, m=5, m=9 составит 𝑃зр(при 𝑚=5)=1−(1−𝑃р)6, 𝑃зр(при 𝑚=5)=1−(1−0,5078)6=0,9857. 𝑃зр(при 𝑚=5)=1−(1−𝑃р)6, 𝑃зр(при 𝑚=5)=1−(1−0,5102)6=0,9861. 𝑃зр(при 𝑚=8)=1−(1−𝑃р)9, 𝑃зр(при 𝑚=8)=1−(1−0,6136)10=0,9995. |
