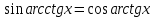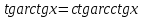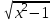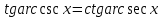открытый урок интегрированная функция. урок интегрирование тригонм функций. Интегрирование тригонометрических функций
 Скачать 184.15 Kb.
|
|
Интегрирование тригонометрических функций Цель: формирование знаний, умений и навыков вычислять интегралы тригонометрических функций; развитие умений анализировать; воспитание целеустремленности Ход урока Организационный момент Актуализация знаний При вычислении интегралов широко применяются всевозможные подстановки, при которых аргумент заменяется функцией от другого аргумента. Разумный выбор подстановки часто позволяет свести задачу к типовому варианту, не требующему особых усилий. Сам же выбор подстановки часто балансирует на грани искусства. Не существует универсальных методов и подстановок, позволяющих решать любой решаемый интеграл. Изучение нового материала При преобразовании подынтегральных тригонометрических функций к алгебраическому виду применяются обратные тригонометрические функции. К примеру:  (1) Эти формулы абсолютно очевидны. В них прямые и обратные функции одноимённы. Переход от тригонометрических функций к алгебраическим с помощью неодноимённых обратных тригонометрических функций не столь же очевиден, хотя и возможен. Такой переход выполняется в рамках обычных тригонометрических преобразований. Покажем конкретные примеры таких преобразований: 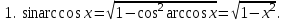 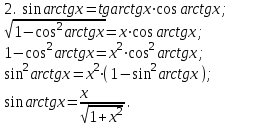 3. Совершенно аналогично получается формула  .  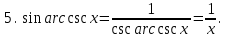Полный свод таких преобразований представлен в таблице 1. Таблица 1 Таблица преобразований тригонометрических функций к алгебраическому виду
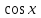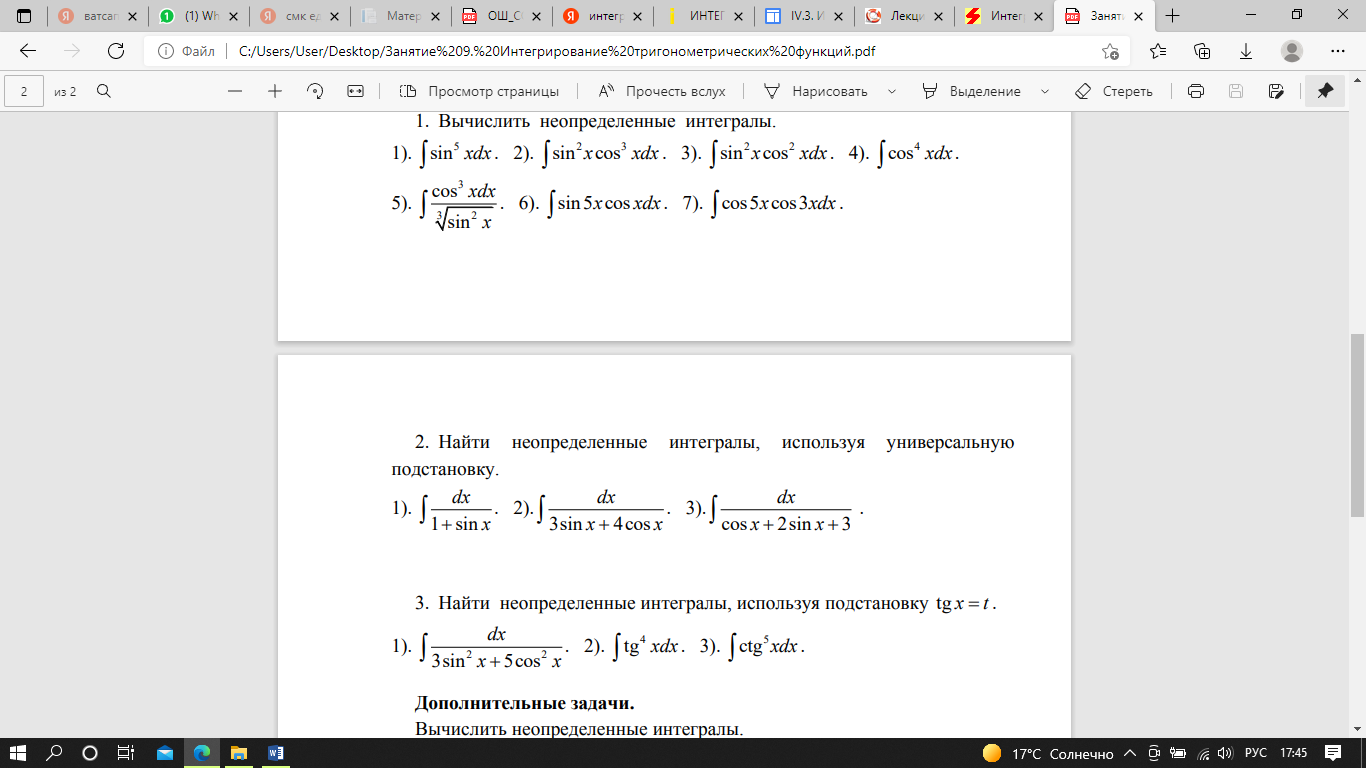Интегрирование элементарных тригонометрических функций  и  с помощью одной из шести обратных тригонометрических функций, интересно лишь с дидактической точки зрения, даёт каждый раз тривиальный результат: (2)Закрепление  Подведение итогов. Рефлексия |
