вычмат лаба 2. Интерполяция непрерывной функции кубическими полиномами (кубическим сплайном дефекта 1)
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
 МИНОБРНАУКИ РОССИИфедеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технологический университет «СТАНКИН» (ФГБОУ ВО «МГТУ «СТАНКИН») Лабораторная работа №2 по дисциплине «Вычислительная математика» Тема: «Интерполяция непрерывной функции кубическими полиномами (кубическим сплайном дефекта 1)» Вариант №14 Выполнил: студент группы ИДБ-19-06 Макаров М.А. Преподаватель: Красикова Е.М. Москва, 2021 Постановка задачи: Пусть на некотором отрезке [𝑎, 𝑏] действительной оси существует некоторая непрерывная функция y(x), значения которой известны лишь в n+1 точке данного отрезка, которые обозначим через 𝑥𝑖 , 𝑖 = 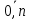 , и 𝑥𝑖 = 𝑎 + 𝑖ℎ, , и 𝑥𝑖 = 𝑎 + 𝑖ℎ, 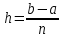 , 𝑥0 = 𝑎, 𝑥𝑛 = 𝑏. Требуется найти для каждых двух соседних точек (узлах) 𝑥𝑖 , 𝑥𝑖+1, 𝑖 = , 𝑥0 = 𝑎, 𝑥𝑛 = 𝑏. Требуется найти для каждых двух соседних точек (узлах) 𝑥𝑖 , 𝑥𝑖+1, 𝑖 = 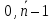 данного отрезка кубический полином, аппроксимирующий данную функцию в каждой точке интервала (𝑥𝑖 , 𝑥𝑖+1 ), значения которого совпадают со значениями функции на концах интервала. данного отрезка кубический полином, аппроксимирующий данную функцию в каждой точке интервала (𝑥𝑖 , 𝑥𝑖+1 ), значения которого совпадают со значениями функции на концах интервала.Необходимо получить кубический сплайн дефекта 1 для функции cos*3(x/3) на отрезке функции [−1;1], построить график сплайна и cos*3(x/3) на одной координатной плоскости для сравнения определить погрешность построенного сплайна Практическая частьДля построения данного сплайна необходимо разредить отрезок [−1;1] на несколько равных отрезков. Пусть данный отрезок будет разделен на 5 равных отрезков. Тогда шаг такого разделения будет равен 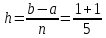 = 0,4. = 0,4.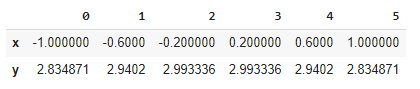 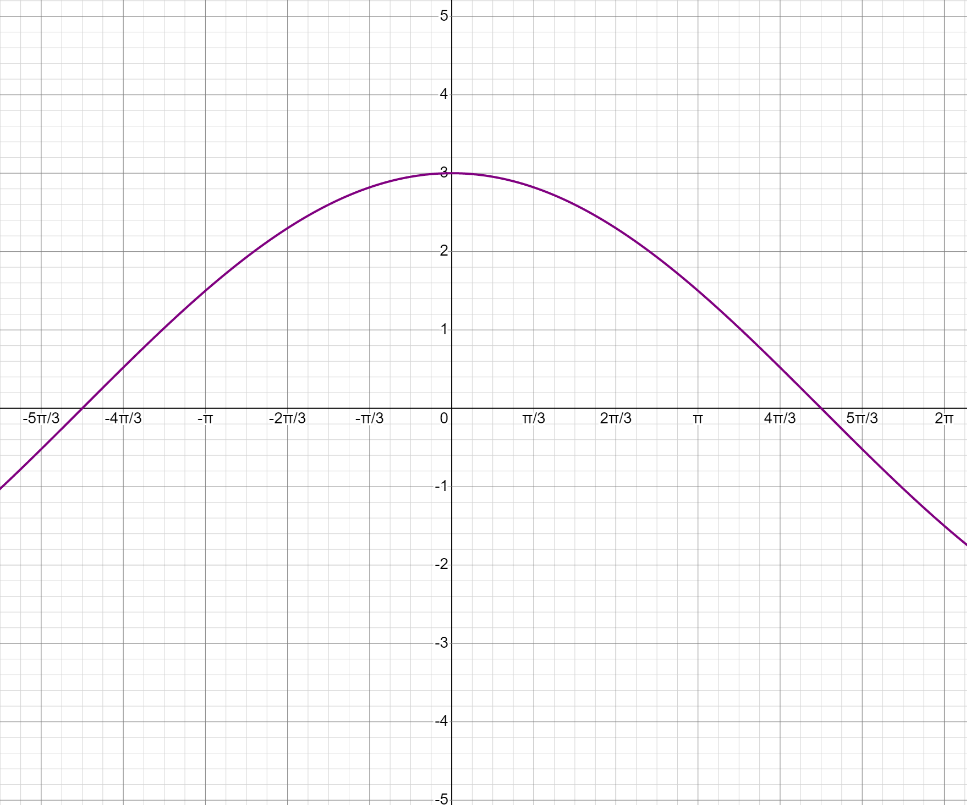 Н  азовем кубическим сплайном функции 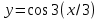 , [-1;1] на сетке точек, указанных в таблице выше, функцию S(x), удовлетворяющую следующим условиям: , [-1;1] на сетке точек, указанных в таблице выше, функцию S(x), удовлетворяющую следующим условиям:Запишем полиномы Si(x) и их производные в виде: 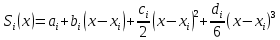 Возьмём первую и вторую производную нашего полинома: 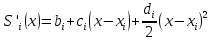 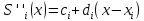 Подставим xi вместо x и получим: 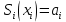 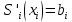 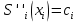 Отсюда следует, что для выполнения третьего условия в узлах интерполяции: 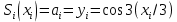 , при i=1,2,3,4,5 , при i=1,2,3,4,5Требуя непрерывности сплайна в узлах xi, i = 1,2,3,4 и выполнения третьего условия при i = 0, получаем: 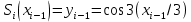 , при i=1,2,3,4,5 , при i=1,2,3,4,5Или 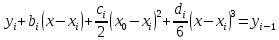 , при i = 1,2,3,4,5 , при i = 1,2,3,4,5Второе условие относительно непрерывности первой производной сплайна в узлах xi, i = 1,2,3,4 приводит к соотношению: 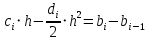 , i = 2,3,4,5. , i = 2,3,4,5.Аналогично, для второй производной сплайна: 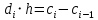 , i = 2,3,4,5. , i = 2,3,4,5.Дополнительные граничные условия (четвертое условие) дают последних два уравнения: 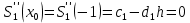 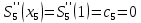 В итоге получается система, содержащая в сумме 3*5 = 15 линейных алгебраических уравнений для отыскания 3*5 = 15 неизвестных: bi, ci, di, i = 1,2,3,4,5. Реализация метода Гаусса: #include #include #include using namespace std; int main() { setlocale(LC_ALL, "RUS"); int i, j, n, m, k; float d; //создаем массив cout << "Кол-во уравнений в системе: "; cin >> n; cout << "Кол-во переменных: "; cin >> m; m += 1; float** matr = new float* [n]; for (i = 0; i < n; i++) matr[i] = new float[m]; //вводим элементы матрицы for (i = 0; i < n; i++) for (j = 0; j < m; j++) { cout << " Элемент " << "[" << i + 1 << " , " << j + 1 << "]: "; cin >> matr[i][j]; } //выводим матрицу cout << "Матрица: " << endl; for (i = 0; i < n; i++) { for (j = 0; j < m; j++) cout << matr[i][j] << " "; cout << endl; } cout << endl; //Метод Гаусса //Прямой ход, приведение к верхнетреугольной матрице float* X = new float[m]; for (i = 0; i < n; i++) { d = matr[i][i]; for (j = n; j >= i; j--) matr[i][j] = matr[i][j] / d; for (j = i + 1; j < n; j++) { d = matr[j][i]; for (k = n; k >= i; k--) matr[j][k] -= d * matr[i][k]; // Диагональная матрица } } //обратный ход // считаем корни X[n - 1] = matr[n - 1][n]; for (i = n - 2; i >= 0; i--) { X[i] = matr[i][n]; for (j = i + 1; j < n; j++) X[i] = X[i] - matr[i][j] * X[j]; } //Вывод решения for (i = 0; i < n; i++) cout << "X" << i + 1 << " = " << X[i] << endl; cout << endl; delete[] matr; return 0; } Исходная система 15х15:  Упрощение и основная матрица 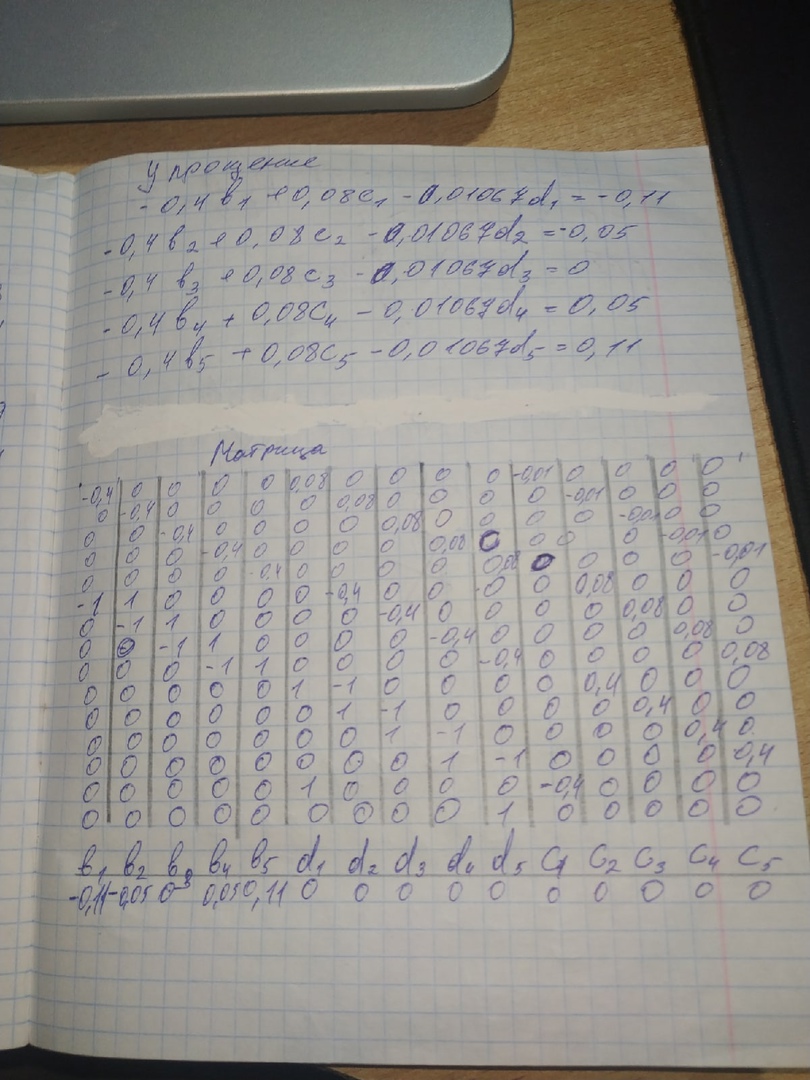 Решаем данную систему методом Гаусса и получаем следующие корни: b1 = 0.2092105283284274 b2 = 0.0552631527008294 b3 = -0.05526315270082938 b4 = -0.2092105283284274 b5 = -0.3078947512551961 с1 = -0.4934211146338432 с2 = -0.2763157635041469 с3 = -0.2763157635041469 с4 = -0.49342111463384336 с5 = -4.336808689942016e-17 = 0 d1 = -1.2335527865846057 d2 = 0.5427633778242403 d3 = -0.0 d4 = -0.5427633778242417 d5 = 1.2335527865846085 a1 = 2.940199733523725 a2 = 2.993335802103367 a3 = 2.993335802103367 a4 = 2.940199733523725 a5 = 2.834870838944213 Подставив данные коэффициенты в изначальное уравнение сплайна, мы получим пять сплайнов, каждый для своего диапазона 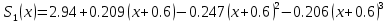 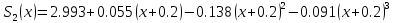 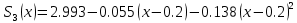 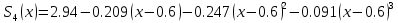 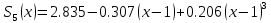 График сплайна 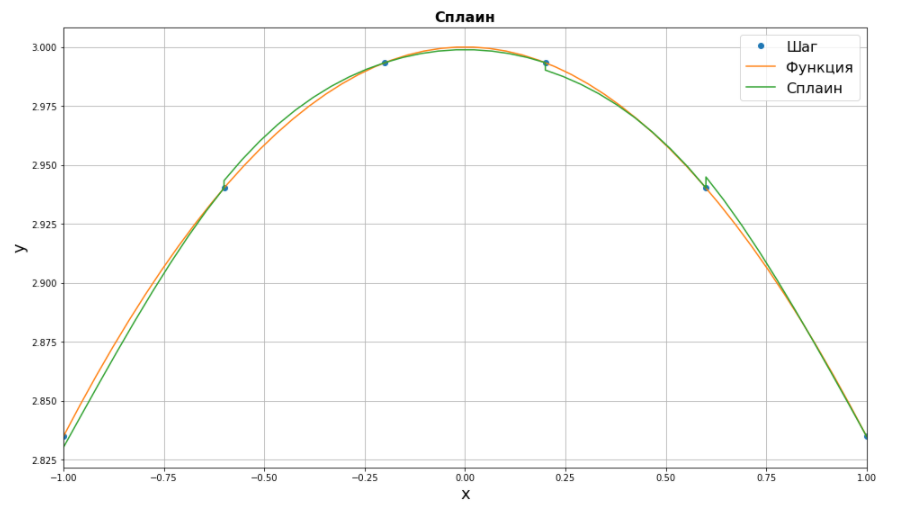 Подсчёт погрешности 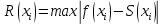 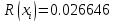 Вывод В данной лабораторной работе мы разобрали интерполяцию кубическим сплайном дефекта 1. Попрактиковались на предложенной функции, построили график сплайна и оценили погрешность данного метода. |
