Зачет № 2 по теме «Перпендикулярность прямых и плоскостей».
Часть 2 К-1
2)Доказать теорему о трех перпендикулярах (прямую или обратную).
3)Один конец данного отрезка лежит в плоскости β, а другой находится от нее на расстоянии 6м. Найти расстояние от середины данного отрезка до плоскости β.
4) Из вершины В треугольника АВС, сторона АС которого лежит в плоскости 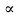 , проведен перпендикуляр ВВ1. Найдите расстояние от точки В до прямой АС и плоскости , проведен перпендикуляр ВВ1. Найдите расстояние от точки В до прямой АС и плоскости 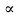 , если АВ=2см, , если АВ=2см, 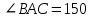 0 и двугранный угол ВАСВ1 равен 450. 0 и двугранный угол ВАСВ1 равен 450.
|
Часть 2 К-2
2)Как расположена прямая к плоскости, если она параллельна прямой, перпендикулярной данной плоскости? (Доказать)
3) АВСD-ромб, к его плоскости проведен перпендикуляр МО, где т.О- точка пересечения диагоналей ромба. Найти расстояние от т. М до ближайшей вершины ромба, если АС=12м, ВD=10м и МО=12м.
4)Через вершину прямого угла С прямоугольного треугольника АВС проведена плоскость, параллельная гипотенузе, на расстоянии 1м от нее. Проекции катетов на эту плоскость равны 3м и 5м. Найти гипотенузу.
|
Часть 2 К-3
2)Доказать свойство двух прямых, перпендикулярных к одной плоскости.
3) Точка А находится на расстоянии2м от вершин равностороннего треугольника со стороной 3м. Найти расстояние от точки А до плоскости треугольника.
4)Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости 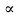 , а катет наклонен к этой плоскости под углом 300. Найти угол между плоскостью , а катет наклонен к этой плоскости под углом 300. Найти угол между плоскостью 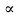 и плоскостью треугольника. и плоскостью треугольника.
|
Часть 2 К-4
2) Определение перпендикулярных плоскостей. Доказать признак перпендикулярности плоскостей.
3) АВСD-квадрат, к его плоскости проведен перпендикуляр ВМ. Найти DМ, если АВ= 2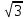 м, ВМ=5м. м, ВМ=5м.
4) Из точки, отстоящей от плоскости на расстояние а, проведены две наклонные, образующие с плоскостью углы 450, а между собой угол 1200. Найти расстояние между основаниями наклонных.
|
Часть 2 К-5
2) Определение прямоугольного параллелепипеда. Записать его свойства. Доказать свойство диагоналей.
3)Из точки к плоскости проведены две наклонные, равные 10см и 17см. Разность проекций этих наклонных равна 9см. Найти проекции наклонных.
4)Ребро СМ тетраэдра АВСМ перпендикулярно к плоскости АВС, АВ=ВС=АС=6м, ВМ=3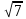 м. Найти двугранный угол МАВС. м. Найти двугранный угол МАВС.
|
Часть 2 К-6
2) Доказать свойство прямой, лежащей в одной из перпендикулярных плоскостей и перпендикулярной их линии пересечения.
3)Через вершину В квадрата АВСD проведена прямая ВК, перпендикулярная к его плоскости. Найдите расстояния от точки К до прямых, содержащих стороны квадрата, если ВК=8дм, АВ=4дм.
4)Общая сторона АВ треугольников АВС и АВМ равна 10см. Плоскости этих треугольников взаимно перпендикулярны. Найти СМ, если треугольники равносторонние.
| |
 Скачать 14.73 Kb.
Скачать 14.73 Kb.