Отчет 2. Интерполяция по узлам Чебышева
 Скачать 399.44 Kb. Скачать 399.44 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В. И. УЛЬЯНОВА (ЛЕНИНА) Кафедра Высшей математики №2 отчет по практической работе №2 по дисциплине «Вычислительная математика» Тема: Интерполяция по узлам Чебышева Студент гр. 6305: Байдуров И. А. Преподаватель: Филатов А.Ю. Санкт-Петербург 2018 г. Задание 1. Построить узлы Чебышева: корни полинома 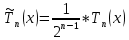 , где , где 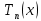 задается рекуррентной формулой: задается рекуррентной формулой: 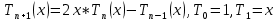 корни 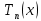 : : 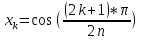 2. Построить интерполяционные полиномы по: равноотстоящим узлам корням Чебышева 3. Посчитать максимум модуля отклонения между исходной функцией и интерполяционным полиномом, построенным по: равноотстоящим узлам корням Чебышева 4. Построить практическое значение максимума модуля отклонения и рассчитать теоретическое. 5. По максимумам модуля отклонения найти 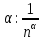 . .Узлы Чебышева.  (Числа в таблице отсортированы по убыванию для наглядности) 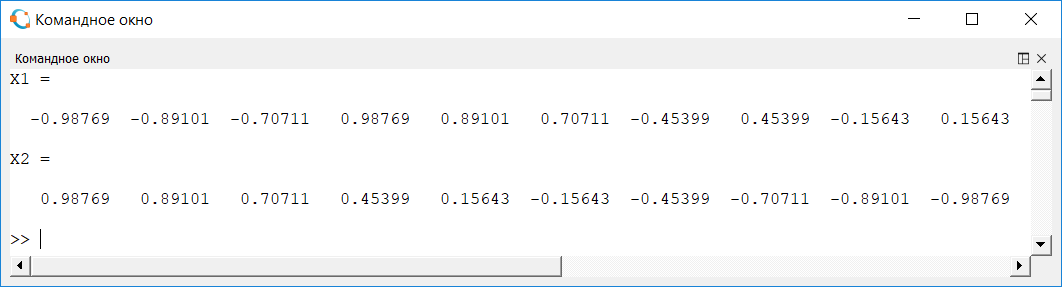
Построить интерполяционные полиномы. 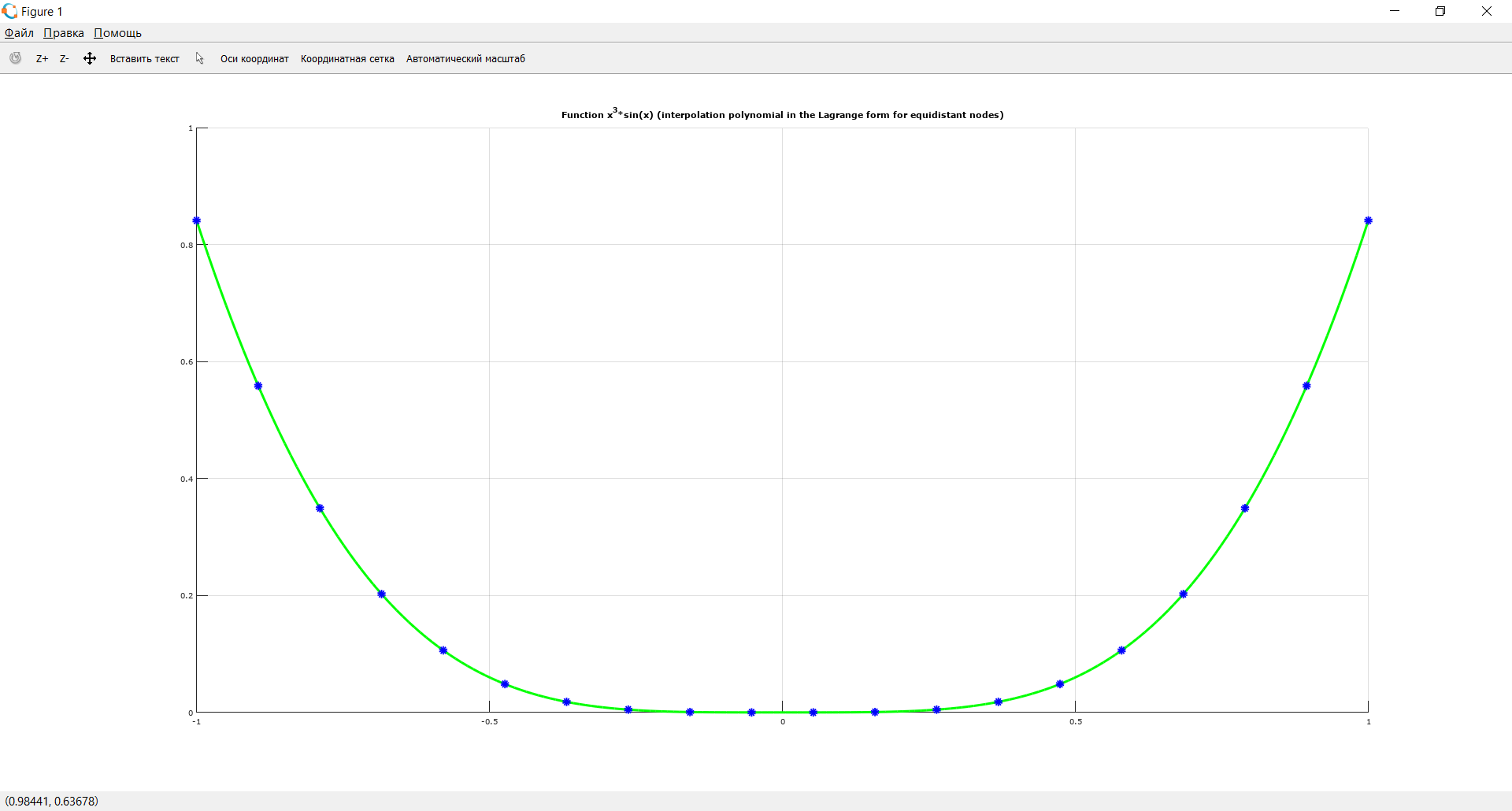 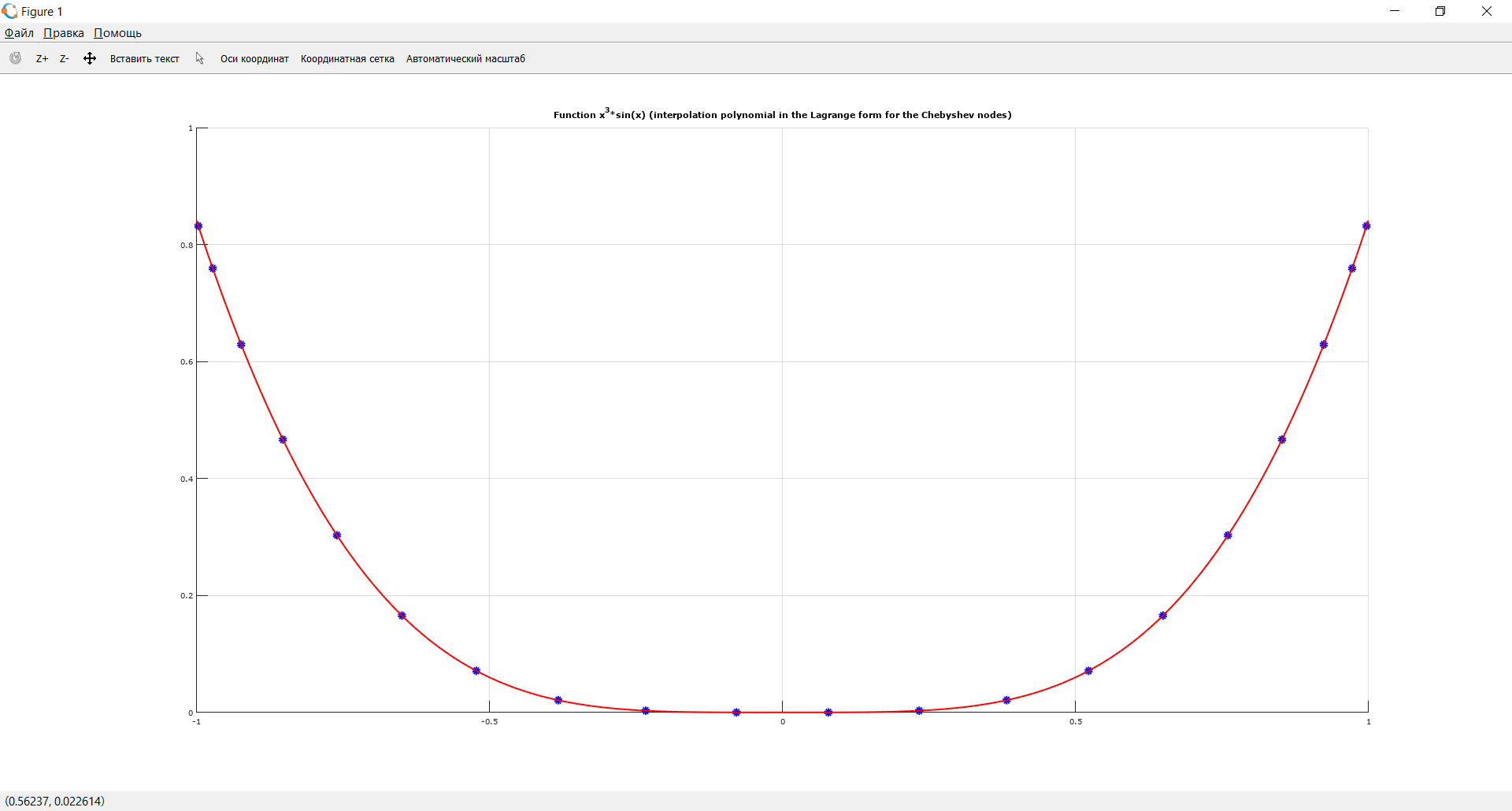 Максимум модуля отклонения между исходной функцией и интерполяционным полиномом. 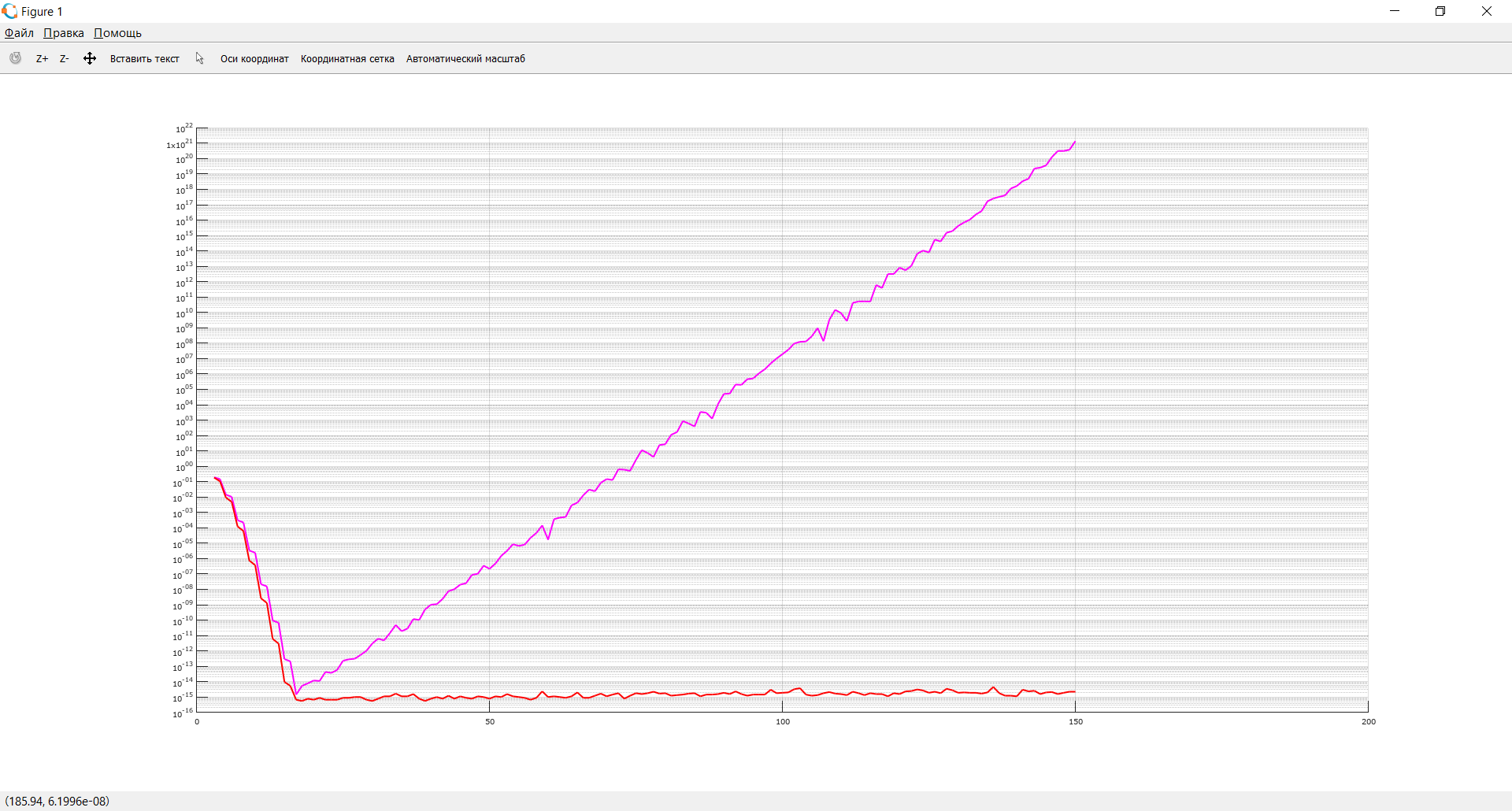 По графику видно, что интерполяционный полином, построенный по равноотстоящим узлам ломается раньше, построенного по узлам Чебышева. Построить практическое значение максимума модуля отклонения и рассчитать теоретическое. Рассчитаем теоретический модуль отклонения (для 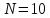 ): ):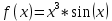 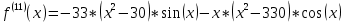 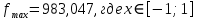 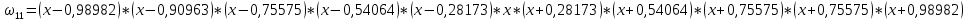 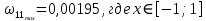 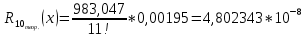 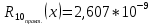 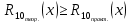 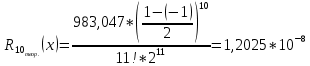 По максимумам модуля отклонения найти 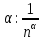 . .При вычислении 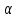 для разных N, была получены следующая зависимость: для разных N, была получены следующая зависимость: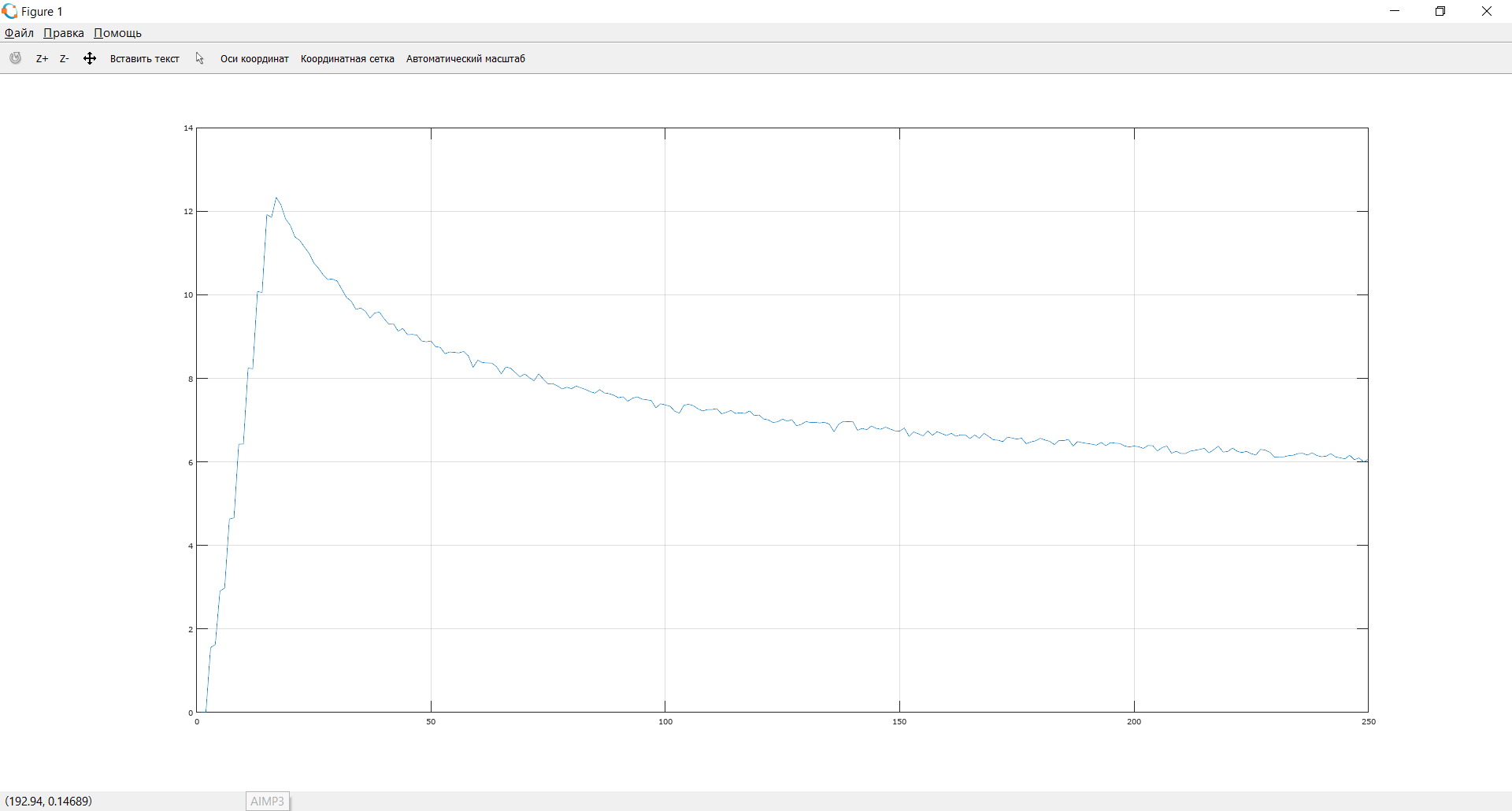 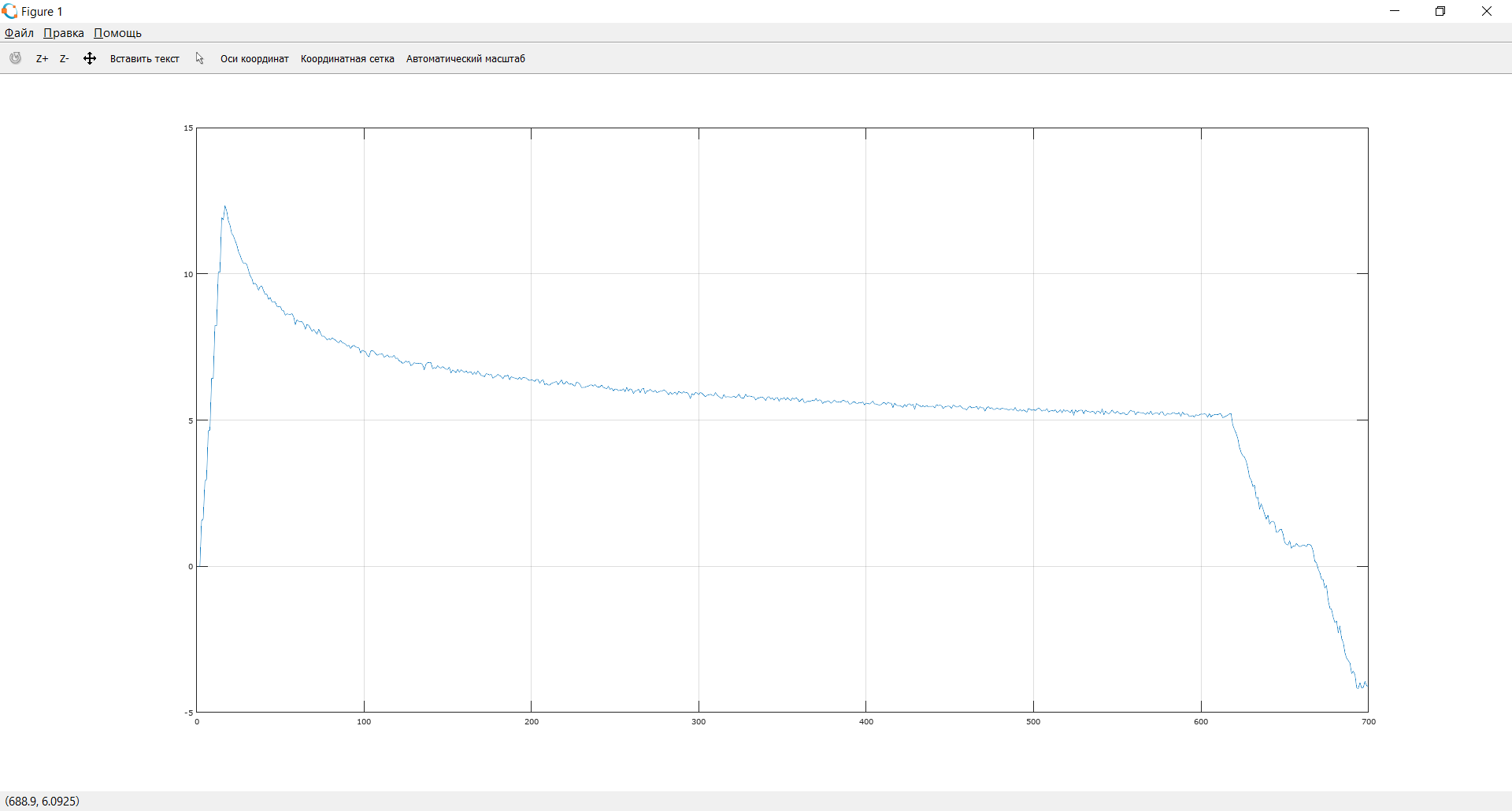 Видим, что 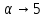 . .Вывод В ходе выполнения данной лабораторной работы было произведено интерполирование функции по узлам Чебышева. Полученный максимум модуля отклонения получился меньше, чем при интерполировании по равноотстоящим узлам. Найдена теоретический максимум модуля отклонения ( 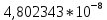 для 10 точек). для 10 точек). |