Вычислительная математика, Сплайны. Отчет. Отчет по лабораторной работе по дисциплине Вычислительная математика Тема Сплайны. Студент гр. 6307 Горст Е. С. Преподаватель
 Скачать 230.89 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ВТ Отчет по лабораторной работе по дисциплине «Вычислительная математика» Тема: Сплайны.
Санкт-Петербург 2018 Цель работы.Выполнить построение кубических сплайнов на промежутке. Сравнить максимальный модуль отклонения от исходной функции и параметр 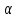 для сплайнов, метода Ремеза, интерполяции по равноотстоящим точкам и по узлам Чебышева методом Лагранжа.Основные теоретические положения.План выполнения работы: На каждом отрезке строим кубический многочлен: 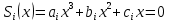 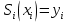 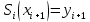 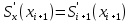 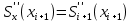 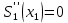 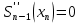 Найти max| 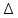 | – максимальный модуль отклонения для 3-20 точек.Найти парметр для 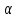для сплайнов, метода Ремеза, интерполяции по равноотстоящим точкам и по узлам Чебышева методом Лагранжа.Экспериментальные результаты.Исходная функция: y = 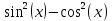 График исходной функции, квази-альтернанса и интерполяционой по Лагранжу.: 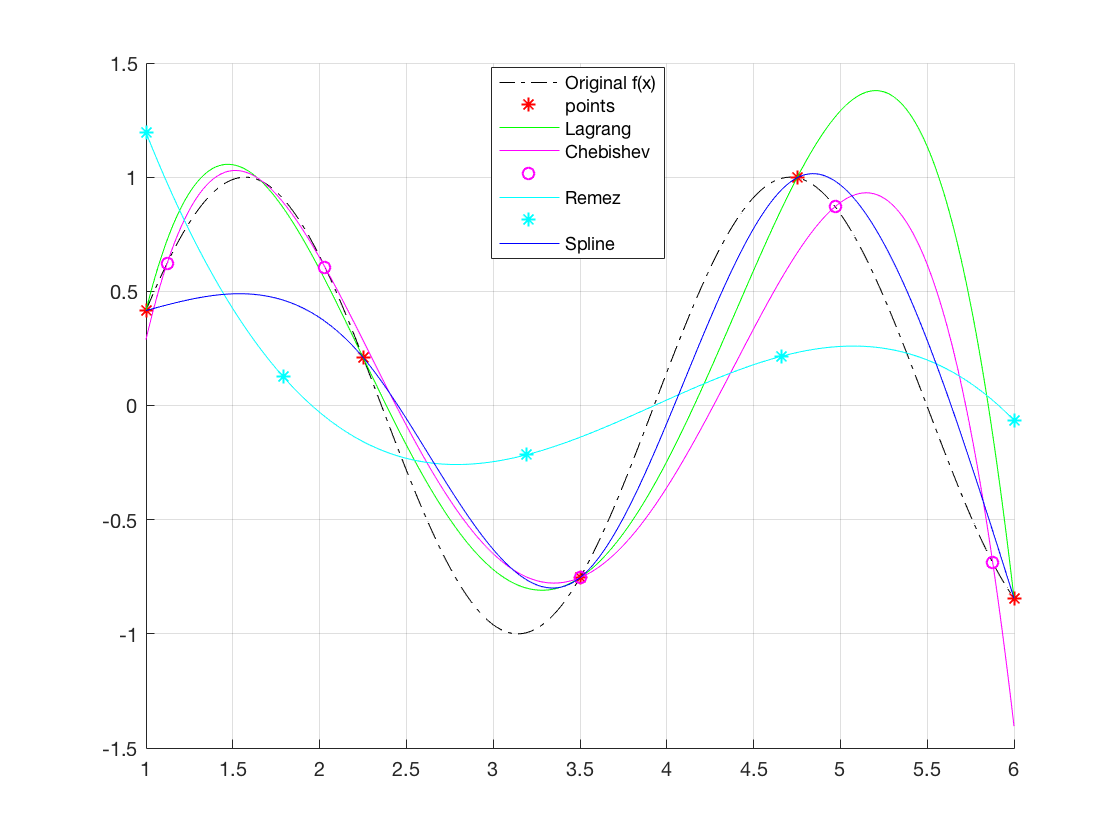  Рис. 1. Графики всех функци. График максимального модуля отклонения сплайнов от исходной функции 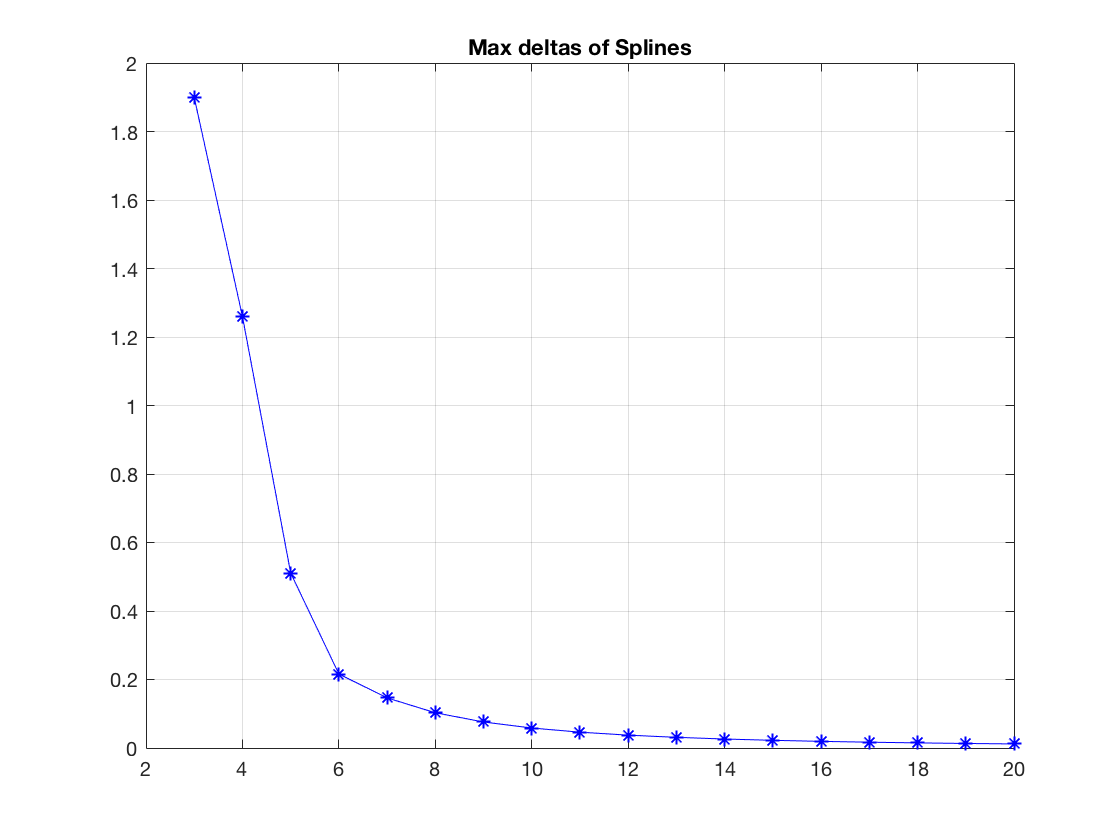 Рис. 2. График максимального модуля отклонения сплайнов от исходной функции. Графики максимального модуля отклонения от исходной функции 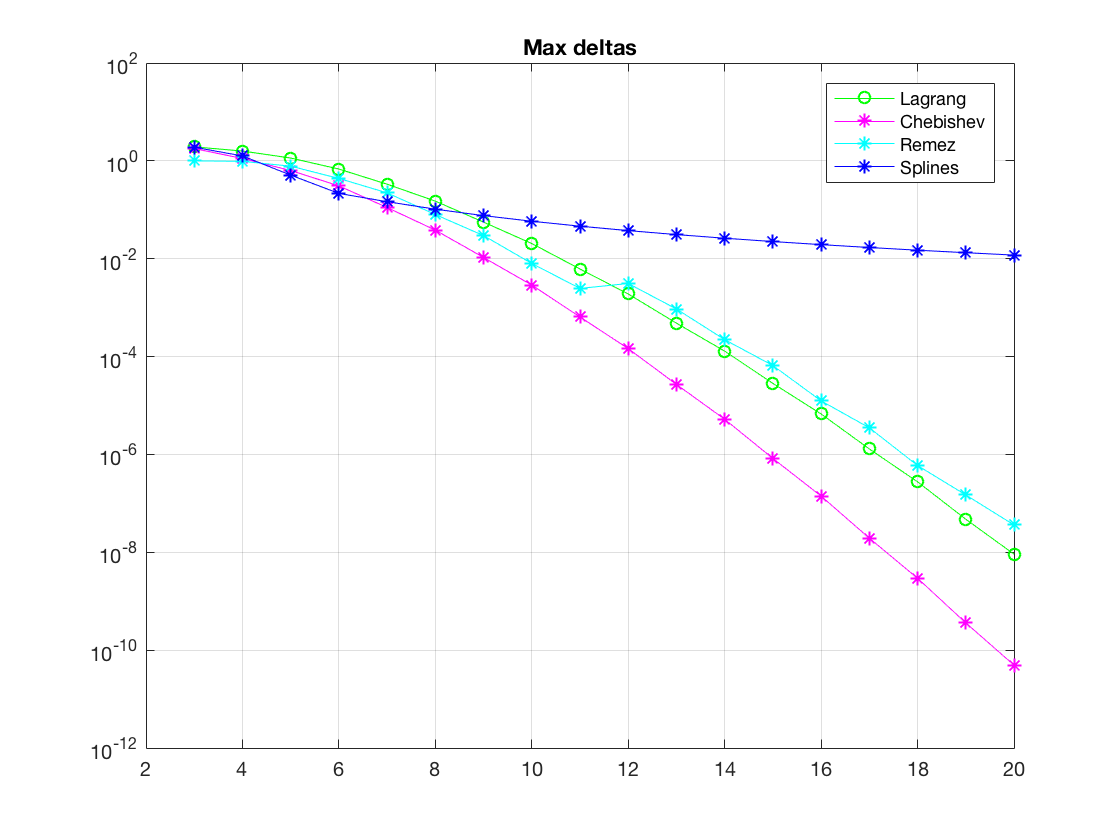 Рис. 3. Графики максимального модуля отклонения от исходной функции. Графики параметров 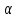 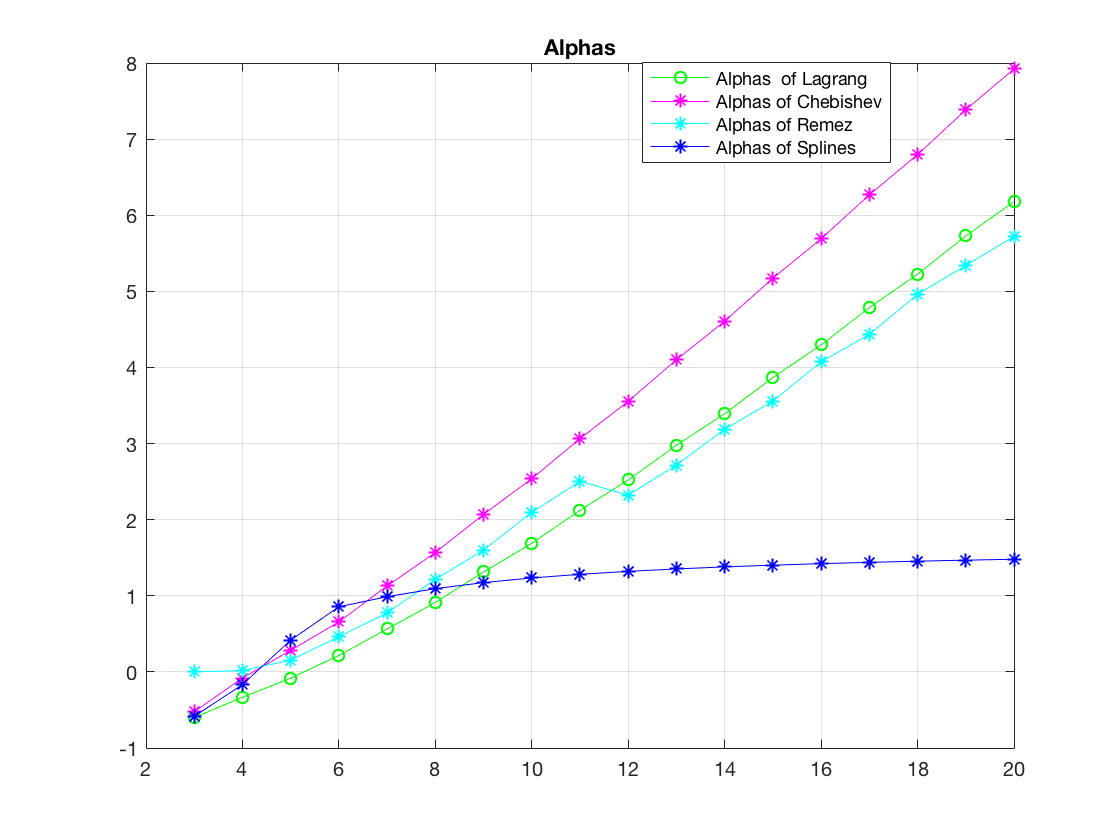Рис. 4. Графики параметров 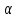.Выводы.В ходе выполнения лабораторной работы была построено очень много различных алгоритмов интерполяции и аппроксимации заданной функции. В итоге оказалось, что лучшее приближение предоставляет все равно чебышев. Все ваши лабы мне нафиг не нужны, я буду пользоваться чебышевым, лучший математик. |