Расчет информационных характеристик источников. Ис ацп к м нк дм цап

• Название: Ис ацп к м нк дм цап
• Дата: 08.06.2022
• Размер: 0.57 Mb.
• Имя файла: Расчет информационных характеристик источников.doc
• Тип: Документы; #577288

ЗАДАНИЕ
Рассчитать основные характеристики системы передачи информации, структурная схема которой дана на рисунке 1.

ИС

АЦП

К

М

НК

ДМ

ЦАП
a(t) j(t_i) b(t) s(t) z(t) 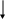к



ДК

ПС




Рисунок 1. Структурная схема системы передачи.
Элементы системы передачи информации:

ИС – источник непрерывного сообщения а(t);

АЦП – аналого-цифровой преобразователь, преобразует сообщение в отсчеты а(t_i), квантованные уровни а_j(t_i) и соответствующие им числа j(t_i) – номера уровней;

К – кодер, выполняет кодирование и образует модулирующий сигнал b(t);

М – модулятор, создает высокочастотный аналоговый сигнал s(t);

НК – непрерывный канал, на выходе которого образуется аддивная смесь z(t) сигнала с помехой;

ДМ – демодулятор, восстанавливает передаваемые кодовые символы к;

ДК – декодер, восстанавливает номера передаваемых уровней ;

ЦАП – цифро-аналоговый преобразователь, восстанавливает квантованные уровни а_j(t_i) и непрерывное сообщение ;

ПС – получатель сообщения.
Исходные данные

№ вар	Уровень, а мин, В	Уровень, а макс, В	Верхняя частота, fв, Гц	№ уровня, j	Вид моду- ляции	Энерг. спектр помехи,N0, В2/Гц	Способ приема
34	0	+6.4	6·10-6	57	ОФМ	1,24·10-9	2

1. ИСТОЧНИК СООБЩЕНИЙ

Источник создает непрерывное сообщение a(t) – случайный квазибелый стационарный процесс, мощность которого сосредоточенна в полосе частот от 0 до fв .

Мгновенные значения сообщения равновероятны в интервале от amin до amax.

1. 
   Функция распределения F(х) мгновенных значений сообщения а(t), плотность распределения w_а(x) и построить их графические изображения.
   

Для отыскания плотности распределения w_а(х) сообщения нужно учесть, что все мгновенные значения сообщения равновероятны в интервале от a_min до a_max


В
Внутри интервала плотность определяется из условий нормировки, вне его равна 0. Аналитическое выражение для плотности вероятности w_а(х), с учетом того, что все мгновенные значения данного случайного процесса в равновероятны, можно записать так:
,
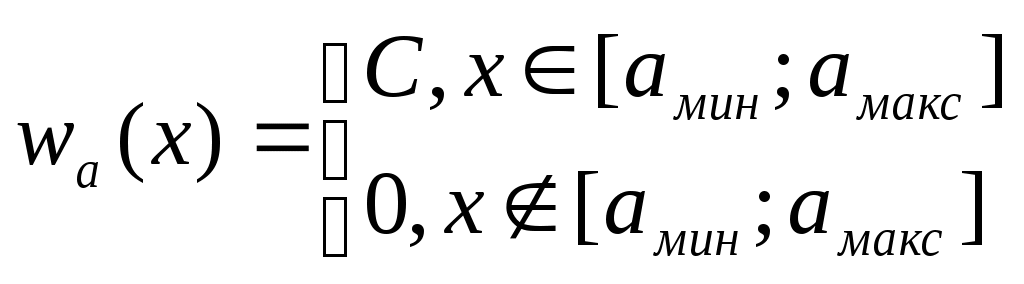С - константа, значение которой можно получить из условия нормировки:

- условие нормировки

=C(a_max-a_min)=1  C= В^-1
Аналитическое выражение для плотности вероятности w_а(х):


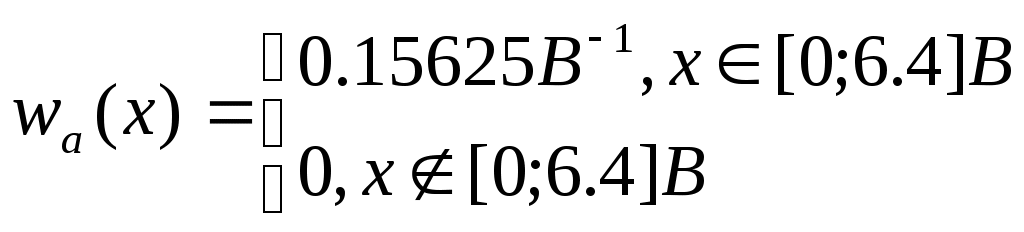
График плотности распределения:



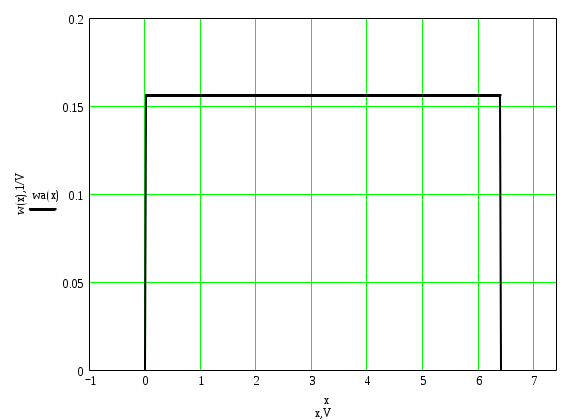
Аналитическое выражение для функции распределения вероятности F_а(х):





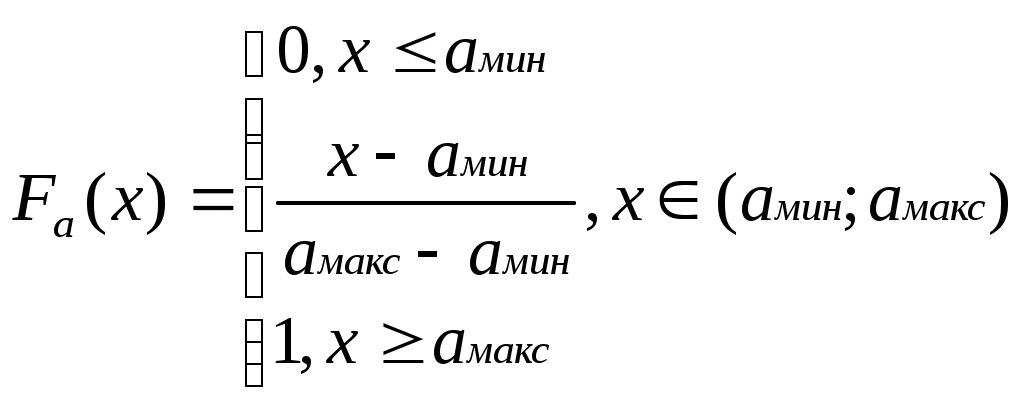
График функции распределения:


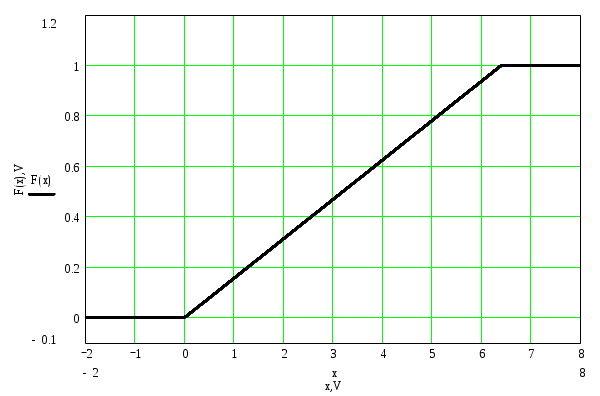
1.2 Расчет математического ожидания m{a(t)} и дисперсии D{a(t)} сообщения a(t).
Математическое ожидание определяется по формуле:
В
Дисперсия D{а(t)} определяется по формуле:

3. 
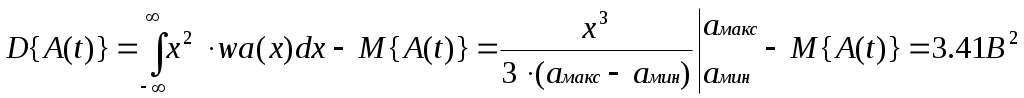
   Расчет постоянной составляющей и мощности Р_а пeременной составляющей сообщения. График для спектральной плотности средней мощности сообщения – энергетический спектр G_a(f).
   

= = 3.2В

PA = D{A(t)} = 3.41В²



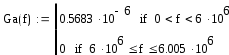
График для спектральной плотности средней мощности сообщения:


1.4 Дифференциальная энтропия сообщения




2. АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ

Передача получателю непрерывного сообщения осуществляется с использованием дискретной системы связи. В процессе подготовки к передаче сообщение подвергается преобразованию в цифровую форму, в поток двоичных символов: нулей и единиц. Преобразование выполняет аналого-цифровой преобразователь (АЦП) в три этапа. На первом этапе производится дискретизация сообщения с постоянным шагом t, т.е. получение непрерывных отсчетов a(t_i). На втором этапе выполняется квантование отсчетов с постоянным шагом а=0,1В. На третьем этапе каждому полученному уровню квантования a_j(t_i) сопоставляется его номер j – число, записанное в двоичной системе счисления, двоичная цифровая последовательность информационных символов.
2.1 Расчет интервала дискретизации t для получения непрерывных отсчетов a(ti) сообщения a(t), ti=it, i = 0, 1, 2, …
По теореме Котельникова: F_д  2f_в  12·10⁶ Гц

Интервал дискретизации: сек.=0.08333 мкс

2.2 Определение числа уровней квантования L, нужных для замены любого непрерывного расчета a(t_i) квантованным отсчетом a_j(t_i), j=0,1,2,… L-1, и далее соответствующим номером уровня квантования j(t_i). Считать, что при квантовании все значения сообщения им любого промежутка a_j ≤а< a_j+1 заменяются нижним уровнем a_j того же промежутка.



2.3 Мощность шума квантования P_шк и ее относительная величина при сравнении с мощностью переменной составляющей непрерывного сообщения.
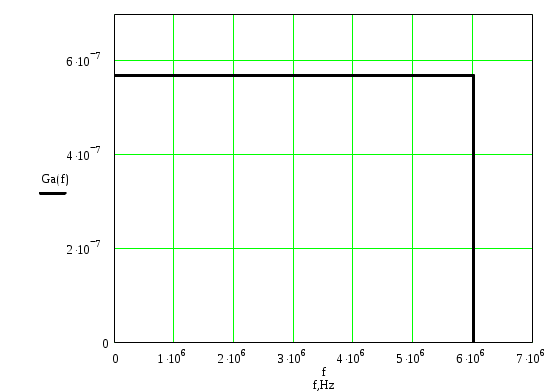
Закон распределения имеет вид, аналогичный закону распределения процесса а(t). То есть можно записать:

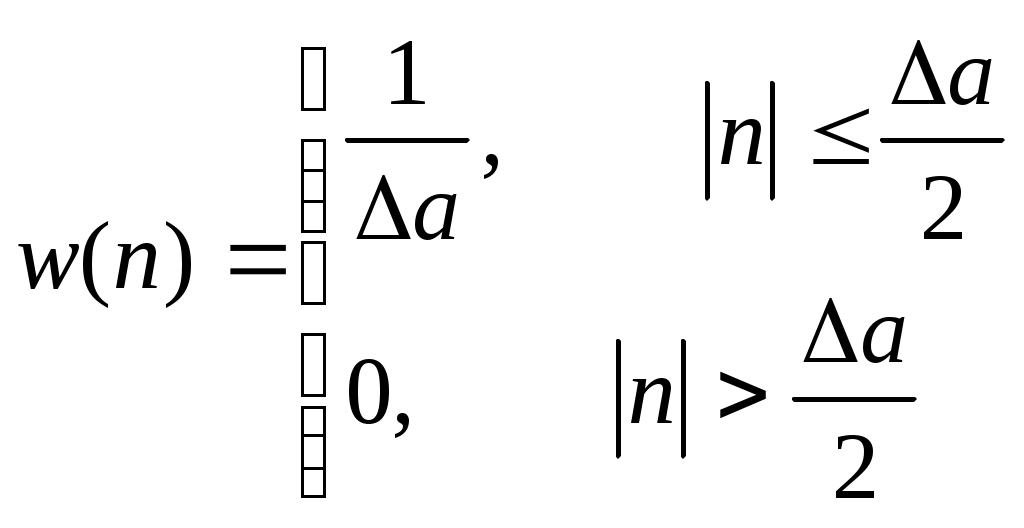
P_шк= 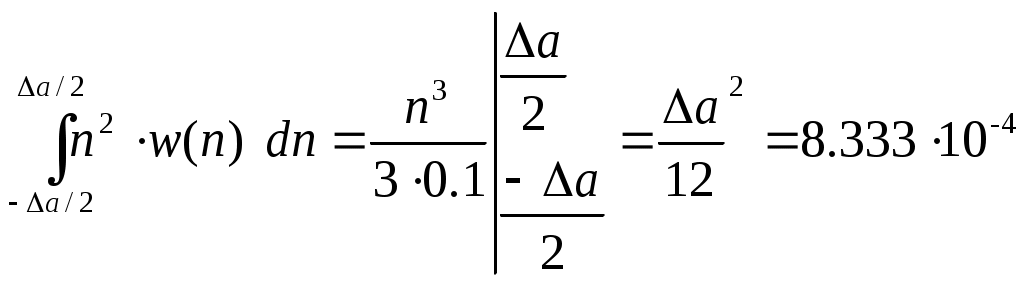B².= 83,3мВ
Определим относительную величину мощности шума квантования по сравнению с мощностью переменной составляющей


2.4 Минимальное число двоичных разрядов k, требуемое для записи в виде двоичного числа любого номера из L номеров уровней квантования:
бит

2.5 k- разрядное двоичное число, соответствующее заданному номеру j уровня квантования a_j:

2.6 Временная диаграмма отклика АЦП на уровень с заданным номером j (в виде последовательности биполярных импульсов):


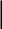
b(t)


1



6T

0

0

T

2T

1

1

1

1


-1

2.7 Энтропия Н и производительность Н′ при условии, что все отсчеты непрерывного сообщения взаимнонезависимы

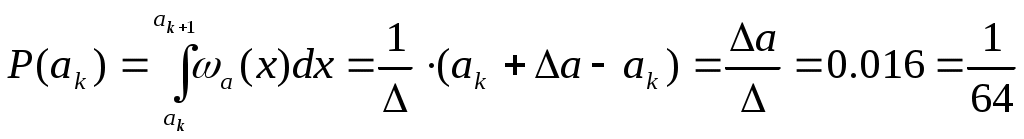
Так как все отсчеты взаимонезависимы, то энтропия АЦП вычисляется по формуле


Производительность АЦП рассчитывается по следующей формуле:




3.кодер

Кодер выполняет систематическое кодирование с одной проверкой на чётность, образуя код (n,k). При этом символы двоичного числа, образованного номером уровня, становятся информационными символами кодового слова. На выходе кодера последовательность кодовых символов b каждого n-разрядного кодового слова b преобразуется в импульсную последовательность b(t) по правилу, приведённому в пункте 6 предыдущего раздела. Длительность импульсной последовательности, соответствующей каждому кодовому слову, одинакова и равна . Сигнал b(t) на выходе кодера представляет собой случайный синхронный телеграфный сигнал.

3.1 Расчёт минимального значения разрядности кода (k) необходимого для примитивного кодирования всех L уровней квантованного сообщения a(ti).

Из теории кодирования известно, что канальным (помехоустойчивым) кодом называется множество из М различных последовательностей x₁, x₂ , x₃,…,x_M одинаковой длины n, каждая позиция которых может принимать любое из m значений входного алфавита Х если M≤mⁿ. Причем при выполнении равенства код является примитивным (безизбыточным), а разрядность кода минимальна. Тогда, в нашем случае, минимальное значение разрядности кода k определим из выражения (учитывая, что - основание кода в нашем случае, а - число возможных последовательностей):



То есть:



Тогда, для осуществления одной проверки на четность, необходимо, чтобы разрядность кода была равна:



3.2 Расчёт избыточности кода с одной проверкой на чётность (æ).

Избыточность кода определяется следующим образом:

æ

3.3 Расчёт двоичной кодовой комбинации, соответствующей передаче a _j -го уровня сигнала.

Будем считать, что при примитивном кодировании - му уровню сигнала ставится в соответствие двоичная кодовая комбинация, представляющая собой запись числа j в двоичной системе счисления. В данном варианте j = 125 .Запишем это число в двоичной системе счисления:



Кодовое слово – вектор .

Определим проверочный символ b₉ путем суммирования по модулю два всех 6 информационных символов данной кодовой комбинации:



, где первые 6 символов – информационные, последний 7-ой – проверочный.

Соответствующая импульсная последовательность имеет вид:



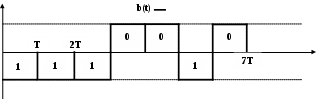
1


-1

3.4 Расчёт числа двоичных символов, выдаваемых кодером в секунду (Vk), и длительности двоичного символа (T).

Число двоичных символов, выдаваемых кодером в секунду, V_K определяется числом отсчетов в секунду (1/Δt) и числом двоичных символов n = k+1 , приходящихся на один отсчет. Длительность двоичного символа Т определяется, как величина обратная V_K:

бит/с=84000кБод



4.модулятор

В модуляторе случайный синхронный телеграфный сигнал производит модуляцию гармонического несущего колебания u(t). Вид модуляции: ОФМ. (Uс=1B, fс=100*Vk = 8.432 ГГц).



График функции корреляции B_b() модулирующего сигнала b(t) имеет вид:


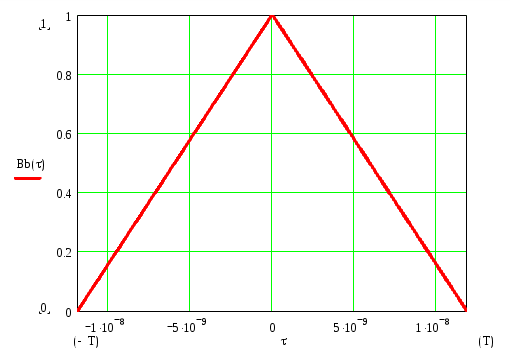
4.2 Выражение и график спектральной плотности мощности G_b(f) модулирующего сигнала b(t):

Функция корреляции Bb() и спектральная плотность мощности Gb(f), как известно из теоремы Хинчина – Винера, связаны парой преобразований Фурье, поэтому Gb(f) можно найти из выражения:



Учитывая, что функция корреляции B_b() есть четная функция от τ, то это выражение можно преобразовать и тогда получаем:





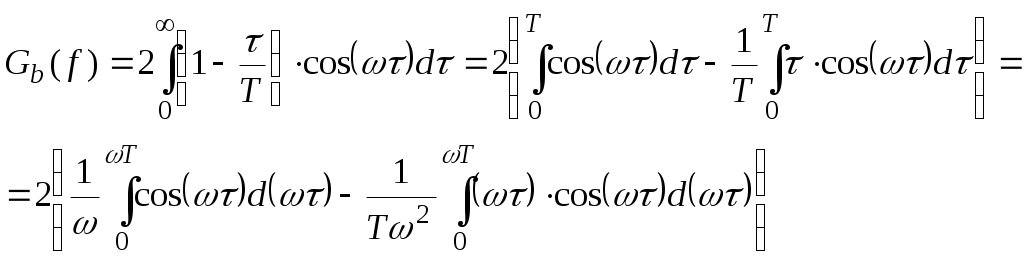
Пусть .

Так как: ,

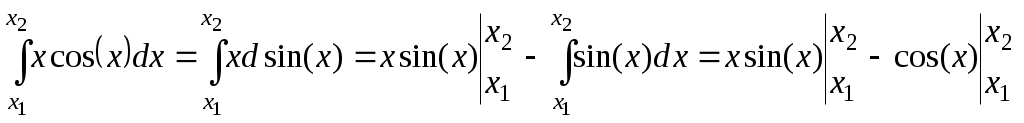То получаем:



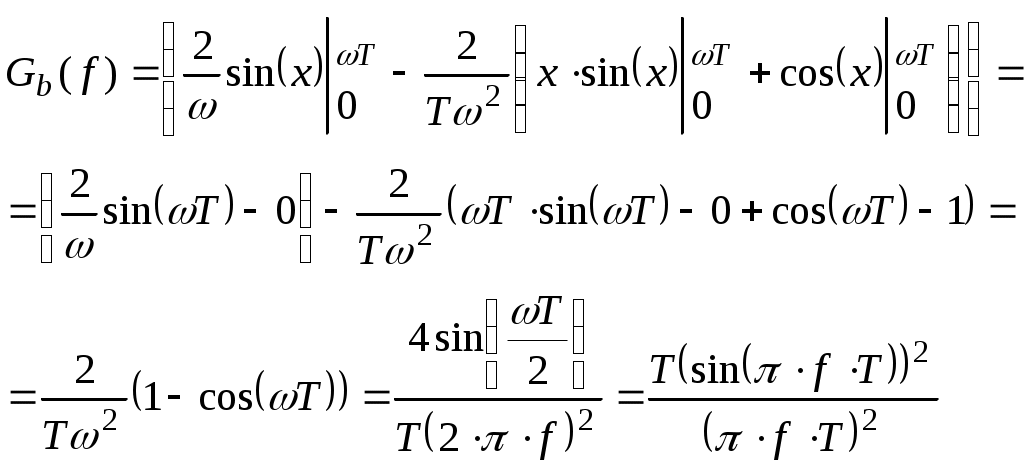
Окончательно:



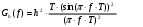
График спектральной плотности мощности G_b(f) имеет вид:



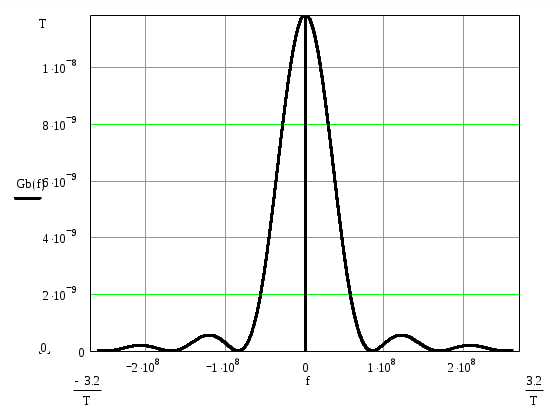
Ограничение спектра модулирующего сигнала производится с целью получения модулированного сигнала с ограниченным спектром. Верхняя частота определяется по формуле (α=2):


=168640 кГц
Гц.

Верхняя частота модулирующего сигнала Fb больше верхней частоты сообщения в раз

График спектральной плотности мощности G_b(f) после ограничения имеет вид:



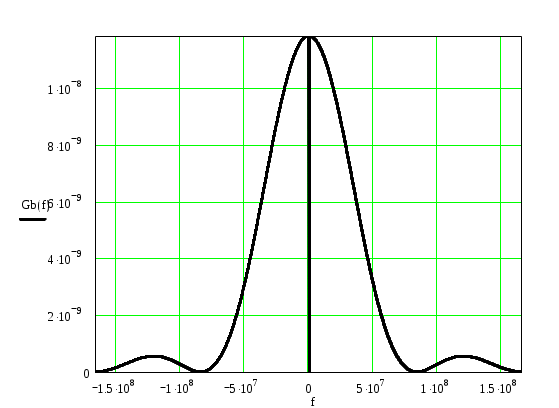
Определим мощность модулирующего сигнала после ограничения спектра. При этом будем исходить из следующих соображений: полная средняя мощность сигнала b(t) (дисперсия) равна значению функции корреляции B_b() в точке 0 (для вычисления интеграла использовалась программа математической обработки данных MathCAD):

Вт

После ограничения верхней частоты спектра модулирующего сигнала его мощность:



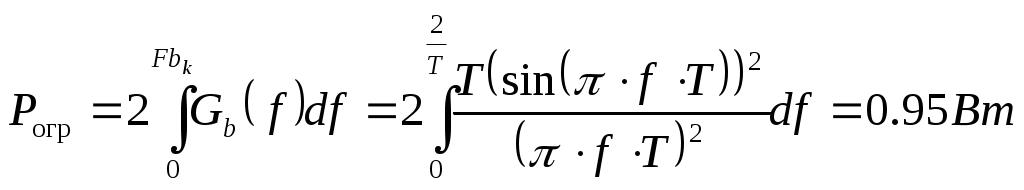
Тогда, отношение средней мощности сигнала в полосе частот от 0 до Fb к полной средней мощности:

%

То есть, в полосе частот от 0 до Fb =1*Vk сосредоточено 95 % средней мощности сигнала.

4.4 Запись аналитического выражения для модулированного сигнала s(t)=F[b(t)] (вид модуляции - ОФМ):

офм(t)=

Модулированный сигнал с ОФМ можно записать как функцию сигнала c(t), который в свою очередь получается в результате перекодировки исходного модулирующего сигнала b(t) по правилу:



Тогда на каждом интервале:



где ,

4 .5 Нарисовать временные диаграммы S(t) ot B(t)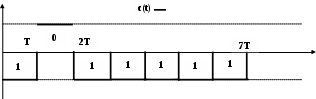











4.6 Выражение и график спектральной плотности средней мощности модулированного сигнала.


=337280 кГц


График спектральной плотности средней мощности модулированного сигнала в области положительных частот.



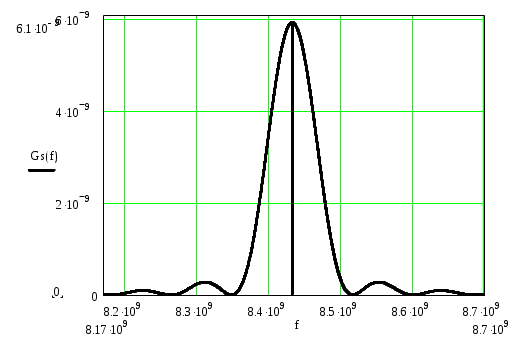
4.7 Ширина спектра Fc модулированного сигнала

Гц

5.нЕПрерывный канал

Передача сигнала s(t) происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии аддитивной помехи n(t). Сигнал на выходе такого канала имеет вид: Z(t)=s(t)+n(t)

Где  - коэффициент передачи канала равный 1.

Помехой является гауссовский шум, у которого спектральная плотность средней мощности постоянна и равна в полосе частот канала Fk.

5.1 Расчёт минимально необходимой ширины полосы частот непрерывного канала

При выборе ширины полосы непрерывного канала необходимо учитывать, что любое расширение полосы пропускания увеличивает мощность помехи, а при не только искажается форма сигнала, но и уменьшается энергия сигнала на выходе канала. Таким образом, минимально необходимая ширина полосы частот непрерывного канала:

= Гц

5.2 Расчёт мощности помехи n(t) на выходе канала.

Мощность помехи в полосе частот Fk = Fс :



5.3 Расчёт отношения Рс/Рn средней мощности сигнала Рс к мощности помехи Рn.

Для двоичных равновероятных сигналов s₁(t) и s₀(t) их средняя мощность равна:



где Е₁ и Е₀ энергия соответственно сигналов s₁(t) и s₀(t):

, .

Для ОФМ сигналов (система с активной паузой):



Тогда:



Примем . Тогда:



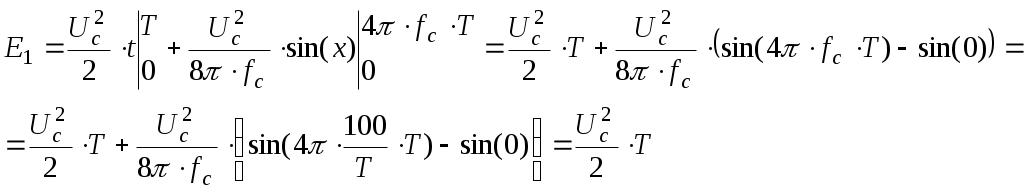
Очевидно, что: .

Средняя мощность сигнала:

Вт.

Отношение Рс/Рn средней мощности сигнала Рс к мощности помехи Рn:



5.4. Расчёт пропускной способности непрерывного канала в единицу времени С:

Пропускная способность непрерывного канала С определяется по формуле Шеннона:

бит/c.=382800кБод

5.5 Эффективность использования пропускной способности непрерывного канала :

Для оценки эффективности использования пропускной способности канала связи применяют коэффициент, равный отношению производительности источника Н’ к пропускной способности канала С’.



6.ДЕМОДУЛЯТОР

Демодулятор, оптимальный по критерию максимального правдоподобия в канале с аддитивной помехой, осуществляет некогерентную обработку принимаемого сигнала Z(t)=S(t)+n(t).

Для двоичной системы правило максимума правдоподобия сводится к проверке неравенства: P(1)*w(z|1)>P(0)*w(z|0) .

Или рассматривают отношение правдоподобий Λ_{i j}:



При равновероятной передаче cимволов и рассмотрении дополнительной “шумовой” гипотезы можно записать отношение правдоподобий:



Тогда правило будет иметь вид:Λ_i > Λ_j при всех i ≠ j

А для двоичной системы правило сведется к проверке:

Λ₁ > Λ₀,

при выполнении этого неравенства регистрируется 1, не выполнении - 0.

0. 
   Алгоритм работы и структурная схема оптимального демодулятора для заданного вида модуляции и способа обработки сигнала.
   

Для двоичной системы передачи сигналов правило оптимального некогерентного приема выражается в неравенством:




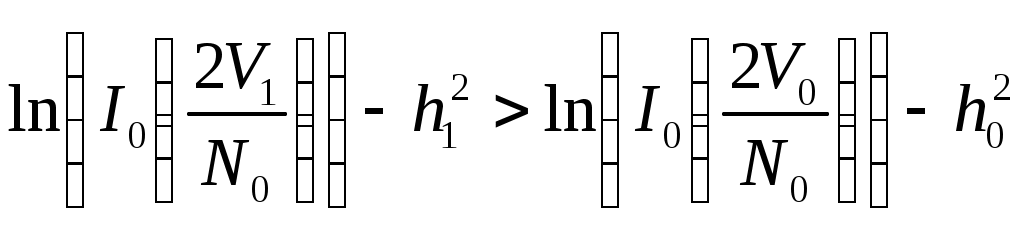
При выполнении данного условия считается, что пришёл сигнал s₁(t) (единица), в противном случае - сигнал s₀(t) (т.е. ноль).

Данный алгоритм и его реализация заметно упрощаются для двоичных систем с ОФМ (система с активной паузой). В этом случае алгоритм сводится к проверке одного неравенства:

.

где:





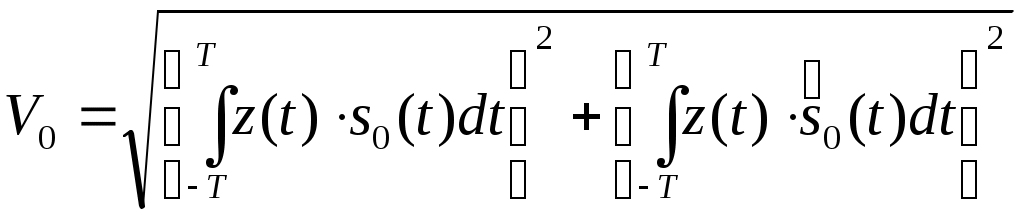
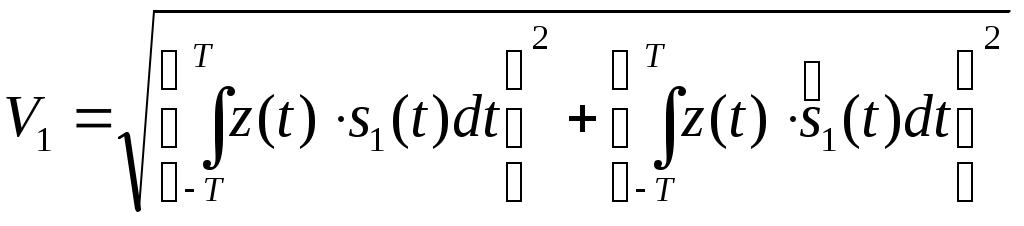
Поскольку при ОФМ информационный параметр сигнала определяется между двумя соседними элементами (на интервале от -T до T).

Для схемной реализации данный алгоритм также можно упростить. Для этого, сначала представим приходящий при ОФМ сигнал s(t) на двух тактовых интервалах в зависимости от символа, передаваемого n-м элементом:

, при передаче символа 0,

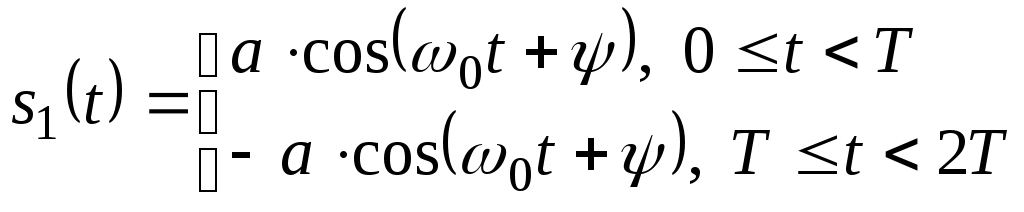, при передаче символа 1,

где - случайная начальная фаза, неизвестная при приеме, зависящая в частности, от символа передавшегося (n-2)-м элементом.

Далее, эти выражения для сигналов и подставим в алгоритм приема и, после сокращения одинаковых слагаемых приведем алгоритм к виду:

, где:

; ;

; .

В случае выполнения неравенства принимается символ 0, в противном случае символ 1.

Из того, что фаза является хотя и случайной, но постоянной на интервале от –T до T, следует, что левая часть полученного алгоритма инвариантна к значению этой фазы.

Структурная схема оптимального некогерентного демодулятора для ОФМ (двоичной системы с активной паузой) на основе активных фильтров в соответствии с имеющимся алгоритмом имеет вид:



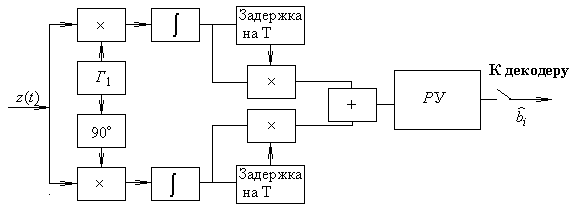
6.3Вероятность ошибки p оптимального некогерентного демодулятора.

Вероятность ошибки p оптимального некогерентного демодулятора при ОФМ определяется следующим выражением:

PОФМ=

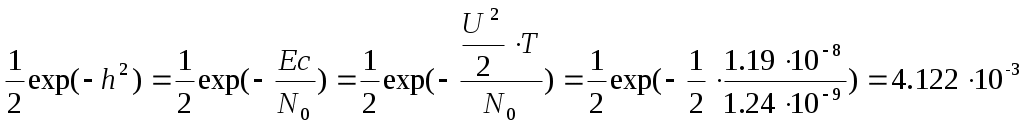
PОФМ=

6.4 Определить, как нужно изменить энергию сигнала (Е), чтобы при других видах модуляции и заданном способе приёма обеспечить вычисленное в п.3 значение вероятности ошибки р.

Так как при частотной модуляции вероятность ошибки определяется выражением:

,

а при амплитудной модуляции:

,

то, очевидно, что для обеспечения вычисленного в п.6.3 значения вероятности ошибки p необходимо при ЧМ увеличить энергию сигнала в 2 раза, при АМ – в 4 раза.

5. 
   Считая выход демодулятора выходом двоичного симметричного канала связи, определить его пропускную способность:
   

Пропускная способность симметричного двоичного канала определяется выражением:

,

где p = p(0/1) = p(1/0) = , бит/с.
Тогда:



кбит/с.

7. декодер

Декодер кода (n,k) анализирует принимаемые последовательности символов длины n и либо преобразует их в последовательность информационных символов k, либо отказывается от декодирования до исправления ошибки. Как и в кодере, работа выполняется в два этапа. На первом этапе производится обнаружение ошибок. Если в принятой последовательности ошибки не обнаружены, то на следующем этапе из неё выделяются k информационных символов – двоичное число, которое передаётся в цифро-аналоговый преобразователь. Если ошибка обнаружена, возможно исправление наименее надёжного символа. Степень надёжности определяется в демодуляторе, сообщение о ней поступает в декодер.

7.1 Оценка обнаруживающей q_o и исправляющей q_u способности кода (n,n-1) с одной проверкой на чётность.

Обнаруживающая и исправляющая способность кодов определяется d_min – минимальным расстоянием по Хеммингу между кодовыми комбинациями.

d_min определяется минимальным весом по всем кодовым комбинациям, отличным от нулевой , в нашем случае d_min = 2 /одна проверка на чётность/.В общем случае: q_omin; q_u ≤ [d_min/2] ( [•] -целое число) , следовательно, q_o=1; q_u=0, т.е. данный код позволяет лишь обнаружить ошибку, но не исправить её.

7.2 Алгоритм обнаружения ошибок.

Код с одной проверкой на чётность получается из примитивного кода добавлением в его конец проверочного символа, который определяется результатом побитного сложения элементов кода по модулю 2, т.е. указывает чётное или нечётное кол-во единиц в примитивном коде. Если в процессе декодирования определяется, что принятая кодовая комбинация имеет нечётный вес, то она считается ошибочной. То есть данный код обнаруживает ошибки только нечётной кратности.

8.ЦИФРО-АНАЛОГОВЫЙ ПРЕОБРАЗОВАТЕЛЬ

В цифроаналоговый преобразователь с декодера поступает k-разрядное двоичное число, восстановленный номер переданного уровня . На первом этапе это число преобразуется в короткий импульс. Амплитуда импульса пропорциональна номеру или восстановленному значению квантованного отсчета . Далее последовательность модулированных по амплитуде импульсов поступает на фильтр – восстановитель, который окончательно вырабатывает из этой последовательности восстановленное сообщение .

8.1 Выражение для амплитуды восстановленного квантованного отсчета ,

соответствующего уровню с принятым номером :

Амплитуда восстановленного квантованного отсчета соответствующего уровню с принятым номером :

В.
8.2 Указать класс фильтра-восстановителя и граничную частоту f_гр его полосы пропускания. Привести формулы и графические изображения частотной и импульсной характеристики фильтра выбранного класса.
Функция фильтра-восстановителя заключается в максимально точном восстановлении формы первичного непрерывного сигнала из ступенчатой функции, создаваемой ЦАП. Из этого следует, что его характеристики должны приближаться к характеристикам идеального ФНЧ, а ширина полосы пропускания соответствовать ширине спектра первичного сигнала: МГц

Фильтр-восстановитель характеризуется комплексной передаточной функцией H(jω).

АЧХ идеального ФНЧ:

|H(jω)| =

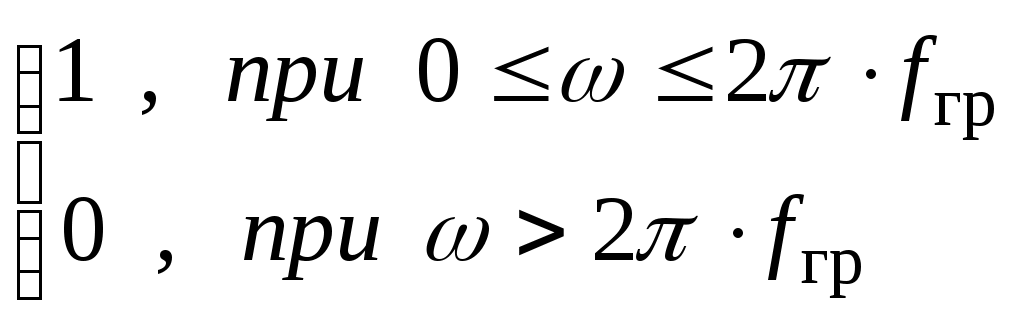
ФЧХ идеального ФНЧ:

θ(ω) = - ωτ , где τ - постоянная (время задержки), параметр, равный по модулю коэффициенту наклона ФЧХ, определяет задержку по времени максимума функции h(t).

Графики АЧХ и ФЧХ идеального фильтра-восстановителя (ФНЧ) имеют вид:

АЧХ



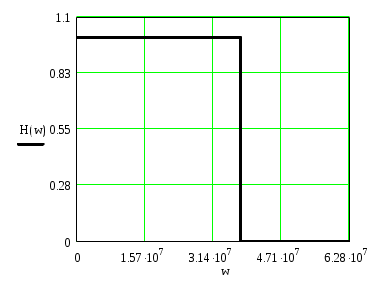
ФЧХ



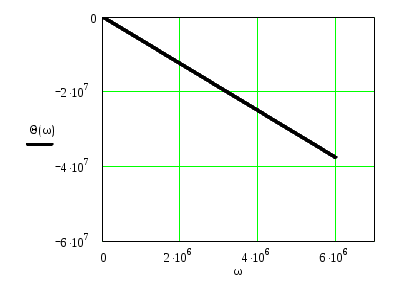
Найдем импульсную реакцию фильтра-восстановителя.





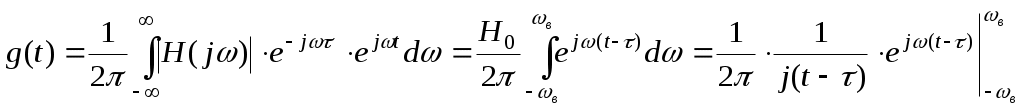
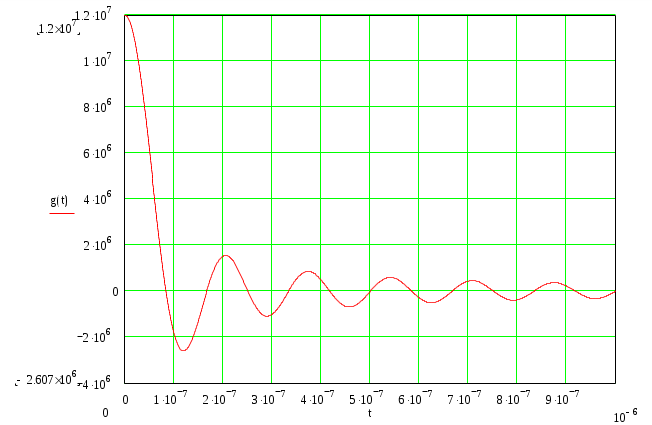
Теорема Котельникова позволяет представить непрерывную функцию в виде ряда

,где