(Исход 1)
Сколько взвешиваний на чашечных весах потребуется, чтобы определить одну фальшивую монету среди семи? (Известно, что фальшивая монета – легче настоящей).
|
(Зачет 1)
Кувшин уравновешивает графин и стакан; 2 кувшина весят столько же, сколько весят 3 чашки; стакан и чашка уравновешивают графин. Сколько стаканов уравновешивает графин?
|
(Исход 2)
Наполненный доверху водой сосуд весит 5 кг, а наполненный наполовину – 3 кг 250 г. Сколько воды вмещает сосуд?
|
(Зачет 2)
Зубр и лось вместе весят 1300кг. Найти вес лося, если 1/6 веса лося равна 1/7 веса зубра.
|
(Исход 3)
В ящике лежат 12 одинаковых шаров, отличающихся только цветом: 6 красных, 3 белых, 2 зеленых и 1 черный. Какое наименьшее число шаров надо взять из ящика наугад, чтобы среди вынутых шаров оказалось хотя бы 3 шара одного цвета?
|
(Зачет 3)
Делимое в 6 раз больше делителя, а делитель в 6 раз больше частного. Чему равен делитель?
|
(Исход 4)
Петя ехал в поезде. Сначала он читал книгу, затем – отдыхал, потом – смотрел в окно, а после – пил чай. На каждое из этих занятий, кроме первого, у Пети ушло вдвое меньше времени, чем на предыдущее. Начал читать книгу он в полдень, а закончил пить чай в час дня. Сколько было времени, когда Петя начал смотреть в окно?
|
(Зачет 4)
Последовательность натуральных чисел строится таким образом. Первое число равно 1. Каждое следующее число получается из предыдущего умножением на 2 и прибавлением к результату 1. Сколько среди первых 2004 членов этой последовательности чисел, делящихся на 5?
|
(Исход 5)
Старший брат идет от дома до школы 12 минут, а младший – 16 минут. Сколько минут потребуется старшему брату, чтобы догнать младшего, если тот вышел на одну минуту раньше?
|
(Зачет 5)
По углам доски 3х3 стоят четыре шахматных коня. За какое наименьшее число ходов коней можно добиться того, что кони вновь займут 4 угловых клетки, причем ни один не останется на своем месте?
|
(Исход 6)
Иван Иванович купил собаку. Саша думает, что эта собака – черный пудель, Паша считает ее белой болонкой, а Маша – белым бультерьером. Известно, что каждый из ребят, верно, угадал либо породу, либо цвет шерсти собаки. Назовите породу собаки, и цвет ее шерсти.
|
(Зачет 6)
Вини-Пух, Сова, Кролик и Пятачок вместе съели 70 бананов, причем каждый из них съел хотя бы один банан. Вини-Пух съел больше всех; Сова и Кролик вместе съели 45 бананов. Сколько бананов съел Пятачок?
|
(Исход 7)
Найдите наименьшее положительное целое число, сумма цифр которого равна 28.
|
(Зачет 7)
На конкурсе за правильный ответ ставили 12 баллов, а за неправильный ответ списывали 10 баллов. Миша ответил на 40 вопросов и набрал 106 баллов. Сколько раз он ответил правильно?
|
(Исход 8)
У Тани и Димы денег поровну. Какую часть своих денег должна Таня отдать Диме, чтобы у него стало в два раза больше, чем у неё?
|
(Зачет 8)
Найти самое маленькое из чисел, которое делится на 7, а при делении на 2, 3, 4, 5, 6 дает остаток 1.
|
(Исход 9)
Укажите следующий после 2002 года «симметричный» год, т.е. читаемый одинаково в обоих направлениях.
|
(Зачет 9)
В комнате стоят табуретки и стулья. У табуреток 3 ноги, у стульев – 4. Когда на всех табуретках и стульях сидят люди, в комнате 39 ног. Сколько в комнате стульев и сколько табуреток?
|
(Исход 10)
Сколько последовательных натуральных чисел, начиная с 1, надо сложить, чтобы получить трехзначное число, записанное тремя одинаковыми цифрами?
|
(Зачет 10)
Количество отсутствующих в классе составляло 1/6 присутствующих. После того, как один из учеников вышел из класса, количество отсутствующих стало составлять 1/5 присутствующих. Сколько учеников в классе?
|
(Исход 11)
Ученик Вовочка любит решать математические задачи. Известно, что вчера он решил 11 задач меньше, чем позавчера и сегодня вместе. Сколько задач решил Вовочка сегодня?
|
(Зачет 11)
Мама купила коробку кускового сахара. Дети сначала съели верхний слой – 77 кусков, затем боковой слой – 55 кусков, наконец, передний слой. Сколько кусочков сахара осталось в коробке?
|
(Исход 12)
Напишите наибольшее девятизначное число, состоящее из различных цифр и кратное 4.
|
(Зачет 12)
Два кита плыли рядом по прямой со скоростью 6 км/ч. Вдруг один из них поплыл быстрее со скоростью 10 км/ч, затем через некоторое время внезапно развернулся и поплыл назад с этой же скоростью. Их расхождение началось в 9.15, а снова киты встретились 10.00.Когда первый кит повернул обратно?
|
(Исход 13)
Коля и Миша разрезали два одинаковых прямоугольника. У Коли получились 2 прямоугольника, каждый периметром 40 см, а у Миши 2 прямоугольника 50 см. Какой периметр имели первоначальные прямоугольники?
|
(Зачет 13)
Сколько существует трехзначных чисел, в названии которых три слова, и все они начинаются с одной и той же буквы?
|
(Исход 14)
Три бобра построили плотину за 12 дней. Весной плотину смыло. Тогда бобры позвали соседей и за 4 дня построили такую же плотину. Сколько помощников позвали бобры?
|
(Зачет 14)
В конкурсе «Русский медвежонок» каждый участник отвечает на 10 вопросов стоимостью 3 балла, 10 вопросов стоимостью 4 балла и 10 вопросов стоимостью 5 баллов. За каждый правильный ответ участник получает количество баллов, равное стоимости вопроса, а за неправильный – 0. Несколько школьников, принимавших участие в конкурсе, обнаружили, что все они набрали разное число баллов. Каким могло быть наибольшее количество ребят?
|
(Исход 15)
В трех ящиках лежат орехи. В первом на 99 орехов меньше, чем в двух других вместе, во втором – на 19 меньше, чем в первом и третьем вместе. Сколько орехов лежит в третьем ящике?
|
(Зачет 15)
На Математической Карусели было 20 исходных и 20 зачетных задач. Команда «УХ» в составе 6 человек решила правильно половину исходных задач. Зачетную задачу с каким наибольшим номером наверняка получила команда?
|
(Исход 16)
Сереже вдвое больше лет, чем будет Саше тогда, когда Толе исполнится столько лет, сколько Сереже сейчас. Кто из мальчиков старший, кто самый младший, кто средний по возрасту?
|
(Зачет 16)
Среди прапрадедушкиных бумаг найден счет: 72 курицы - *61 руб. 9* коп. Первая и последняя цифра суммы, выражавшей стоимость 72 куриц, неразборчивы и заменены звездочками. Сколько стоила одна курица?
|
(Исход 17)
Половина трёхзначного числа нацело делится на 2, треть – на 3, а пятая часть – на 5. Какое это число?
|
(Зачет 17)
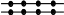 На двух прямых отметили по четыре точки так, как показано на рис. 1 Сколько существует треугольников с вершинами в отмеченных точках? На двух прямых отметили по четыре точки так, как показано на рис. 1 Сколько существует треугольников с вершинами в отмеченных точках?
Рис.1
|
(Исход 18)
В шахматном фестивале участвовало 8 команд. В каждой команде – 5 человек. Турнир прошёл по круговой системе (каждая команда сыграла с каждой по одному матчу). Сколько партий было сыграно на фестивале? (Если команда А встречается с командой В, то 1-ый игрок команды А, играет с 1-ым игроком команды В, второй – со вторым, …, пятый – с пятым).
|
(Зачет 18)
Дорога между двумя горными селами А и В идет то в гору, то под гору. Автобус, который развивает среднюю скорость 30 км/ч в гору и 60 км/ч под гору, проехал из А и В и обратно. Какова была его средняя скорость на всем пути?
|
(Исход 19)
Сэма-пижамчика в корзинке лежат 13 синих, 14 красных и 15 зелёных носков. Сколько носков надо, не глядя, вытащить из корзинки, чтобы среди них наверняка нашлось не менее двух красных и двух зеленых носков?
|
(Зачет 19)
В волейбольном турнире, проходившем в один круг (каждая команда играет с каждой ровно один раз) 20% всех команд не одержали ни одной победы. Сколько команд участвовало в этом турнире? Ничьих в волейболе не бывает.
|
(Исход 20)
В магазине «Зоомир» продают «Вискас» в пакетах по 3 и 5 кг. Всего на полке стоит 24 пакета. Вес всех пакетов по 5 кг равен весу всех пакетов по 3 кг. Сколько было пакетов по 3 кг?
|
(Зачет 20)
В некотором государстве система авиалиний устроена таким образом, что любой город соединен авиалиниями не более, чем с тремя другими, и из любого города в любой другой можно долететь, сделав не более одной пересадки. Какое наибольшее число городов может быть в этом государстве?
|
 Скачать 36.75 Kb.
Скачать 36.75 Kb.