Основы механники подвижного состава. Исходные данные 3 1 Динамика необрессоренных масс тс 5
 Скачать 413.52 Kb. Скачать 413.52 Kb.
|
 СОДЕРЖАНИЕ Исходные данные 3 1 Динамика необрессоренных масс ТС 5 1.1 Силы, действующие в вертикальной плоскости 5 Удар колеса по рельсу в вертикальной плоскости 5 Движение необрессоренной массы по кинематическим неровностям 6 1.2. Силы, действующие в горизонтальной плоскости 8 Удар колеса по рельсу в горизонтальной плоскости 8 Кривые участки пути 10 Устойчивость колес против схода с рельсов 13 2. Динамика в системе необрессоренная – обрессоренная масса 16 Частотная характеристика собственных вертикальных колебаний 16 3 Динамика в системе обрессоренная – обрессоренная массы 21 4 Гасители колебаний 26 Уравнение сил, действующих в диссипативной системе 26 Исходные данные Сцепной вес 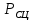 , кН – 1260 , кН – 1260 Количество тележек, шт – 2 Количество колесных пар, шт – 4 Масса (вес) тележки в сборе 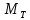 ( (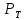 ) , т (кН) – 23,78(233,3) ) , т (кН) – 23,78(233,3)Неподрессоренный вес тележки 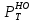 , кН – 110 , кН – 110Нагрузка от колесной пары на рельсы 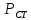 , кН – 210 , кН – 210Жесткость листовой рессоры 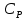 , кН/м – 1246 , кН/м – 1246Статический прогиб листовой рессоры 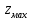 , мм – 65 , мм – 65 Эквивалентная жесткость на одно колесо 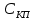 , кН/м – 1100 , кН/м – 1100Жесткость пружины 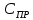 , кН/м – 1600 , кН/м – 1600 Статический прогиб пружины 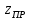 , м – 0,02 , м – 0,02Жесткость пружины центрального подвешивания, кН/м – 3000 Статический прогиб пружины центрального подвешивания, м –0,07 Условный тип гасителя колебаний – гидравлический Высота центра тяжести над уровнем рессорного подвешивания hц, м – 1,55 Момент инерции электровоза относительно оси пути ( ОХ) Iх, кг∙ м2∙109 – 22,6 Момент инерции электровоза относительно оси, перпендикулярной оси пути ( ОZ) IZ, кг∙ м2∙109 – 8,0 Максимальная высота вертикальных неровностей путиh (ƞ), м – 0,015 Длина периода неровностей пути L, м – 25 Приведенная масса пути mП. кг – 130 Угол в стыке рельсов γ, рад – 0,031 Боковая жесткость пути СП, Н/м ∙107 – 2,1 Вертикальная жесткость рельсового пути 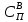 , 103 кН/м – 45 , 103 кН/м – 45Коэффициент эквивалентного вязкого трения в расчете на одну колесную пару βП, кН∙с/м – 340 Максимальный горизонтальный зазор между колесом и рельсом, м – 0,004 Максимальная горизонтальная неровность, м – 0,004 Длина ползуна 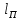 , м – 0,007 , м – 0,007Радиус круговой кривой R, м – 750 Длина переходной кривойlПЕР , м – 80 Полярный момент инерции тележки относительно вертикальной оси Oy, Iy, кг∙ м2∙105 – 8,1 В данной работе я решил рассчитывать секцию локомотива серии ВЛ 80, со следующими параметрами, необходимыми для расчета: База тележки 2 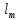 , м – 3,0 , м – 3,0Диаметр бандажа колесной пары DКП, м – 1,25 Вес колесной пары QКП, Н – 19600 База локомотива LЛ, м – 7,5 Расстояние от центра поворота кузова (оси) до центров шкворней 1-ой и 2-ой тележек 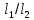 , м – 4/3,5 , м – 4/3,5Высота центра ветровой нагрузки от головки рельса hВ, м – 2,4 Площадь боковой поверхности локомотива FВ, м2 – 80 Высота центра тяжести кузова от головки рельса hЦ.Г., м – 2,3 Разность высот автосцепок ߡhВ, м – 0,1 Длина локомотива LВ, м – 15,2 Расстояние между клиновыми отверстиями автосцепок 2к, м –16,42 1 Динамика необрессоренных масс ТС Силы, действующие в вертикальной плоскости Удар колеса по рельсу в вертикальной плоскости Для определения наибольшей величины сил инерции необрессоренных масс, возникающих при движении колеса радиуса r, с ползуном ln или при прохождении стыка, в котором рельсы при прогибе образуют угол γ, следует воспользоваться формулой: 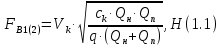 где Vk – скорость удара колеса по рельсу, м/с, определяемая для каждого случая по формулам: - при прохождении стыка: 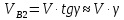 , м/с , м/с- при ползуне: 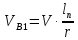 , м/с (1.2) , м/с (1.2)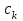 = 4,9·105 – контактная жесткость колеса и рельса, Н/м; = 4,9·105 – контактная жесткость колеса и рельса, Н/м;r – радиус колеса, r = 1,250/2 = 0,625 м; ln = 0,007 м – длина ползуна; γ – угол в стыке рельсов, γ = 0,031 рад; V – скорость ТС (здесь и далее принимаем 100 км/ч 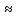 27,8 м/с); 27,8 м/с);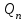 – приведенный вес рельса, Н, – приведенный вес рельса, Н, 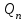 = 130∙9,81 = 1275 Н; = 130∙9,81 = 1275 Н;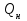 – вес неподрессоренной массы, приходящийся на колесо, Н, – вес неподрессоренной массы, приходящийся на колесо, Н, 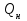 = 110/2 = 55 кН = 55000 Н. = 110/2 = 55 кН = 55000 Н.Подставляя значения в 1.2 получим: 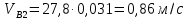 , , 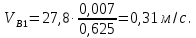 Затем, подставляя значения в 1.1 получим: 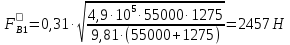 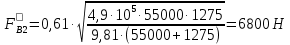 Движение необрессоренной массы по кинематическим неровностям Описывается выражением: 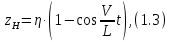 Вертикальная скорость 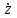 колеса по оси колеса по оси 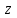 есть первая производная от его перемещения: есть первая производная от его перемещения: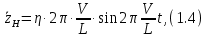 Ускорение вертикальных перемещений 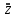 колеса по оси колеса по оси 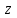 есть вторая производная от его перемещения: есть вторая производная от его перемещения: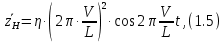 где 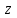 – амплитуда вынужденных колебаний кузова, м; – амплитуда вынужденных колебаний кузова, м;η – амплитуда неровностей пути, м; 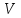 – скорость движения ТС, (по заданию от 10 до 140 км/ч или 2,7-40 м/с); – скорость движения ТС, (по заданию от 10 до 140 км/ч или 2,7-40 м/с);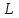 – длина периода неровностей, м. – длина периода неровностей, м.Подставляя данные в функции строим графики зависимости 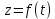 , , 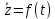 , и , и 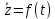 , для 1–2 секунд движения ТС в заданном временном интервале (рисунок 1.1, 1.2, 1.3). , для 1–2 секунд движения ТС в заданном временном интервале (рисунок 1.1, 1.2, 1.3). 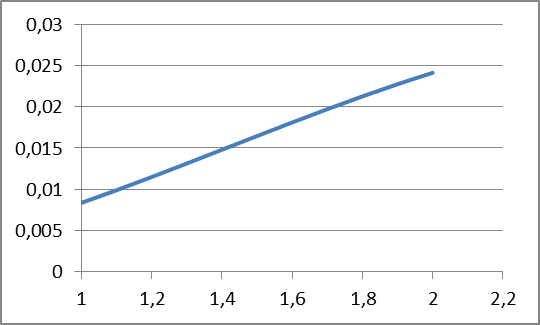 Рисунок 1.1 – Вертикальное перемещение колеса. 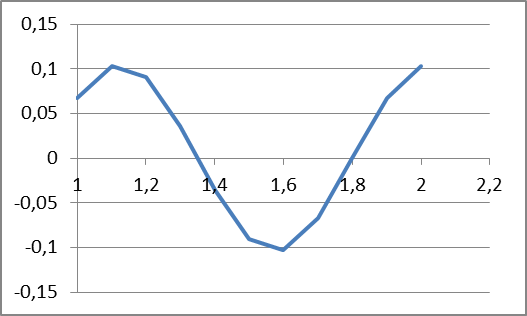 Рисунок 1.2 – Вертикальная скорость колеса.  Рисунок 1.3 – Ускорение вертикальных перемещений. Динамическая сила вследствие кинематических возмущений в вертикальной плоскости: 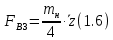 где 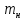 - общая необрессоренная масса тележки, кг (110 кН = 11213 кг). - общая необрессоренная масса тележки, кг (110 кН = 11213 кг).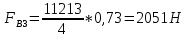 Сумма динамических сил, действующих в вертикальной плоскости: 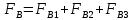 (1.7) (1.7)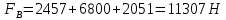 1.2. Силы, действующие в горизонтальной плоскости Удар колеса по рельсу в горизонтальной плоскости Крестовины рассматривают, как геометрические неровности. При одинаковых скоростях сила удара колеса по крестовине при движении по прямой в 3–5 раз больше, чем при вхождении ТС в крутые кривые и стрелочные переводы. Для современных стрелочных переводов при скорости ТС 30 м/с сила удара достигает 300 кН. Движение колеса по крестовине приводит к горизонтальному удару гребня колеса в усовик. Силу удара определяют по формуле: 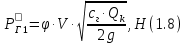 где 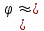 0,03 рад – угол набегания колеса на рельс; 0,03 рад – угол набегания колеса на рельс;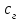 = 105 – контактная жесткость системы колесо – рельс в горизонтальной плоскости поперечно оси пути, Н/м; = 105 – контактная жесткость системы колесо – рельс в горизонтальной плоскости поперечно оси пути, Н/м;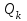 – вес крестовины, Н (14 кН); – вес крестовины, Н (14 кН);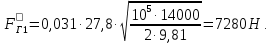 Для расчета наибольшей величины боковой силы 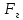 при извилистом движении ТС в прямом участке пути, можно применить формулу: при извилистом движении ТС в прямом участке пути, можно применить формулу: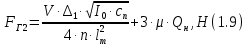 где 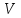 – скорость ТС, 27,8 м/с; – скорость ТС, 27,8 м/с;Δ1 – 0,02 м – максимальный зазор между гребнями колес и рельсами; 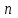 = 0,05 – конусность обода колеса; = 0,05 – конусность обода колеса;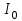 – полярный момент инерции тележки относительно вертикальной оси, кг·м2, I0 = 8,1∙107 кг·м2; – полярный момент инерции тележки относительно вертикальной оси, кг·м2, I0 = 8,1∙107 кг·м2;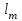 – половина базы тележки, м, lm = 3,0/2 = 1,5м ; – половина базы тележки, м, lm = 3,0/2 = 1,5м ;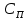 – боковая жесткость пути, Н/м, сn = 2,1∙107 Н/м; – боковая жесткость пути, Н/м, сn = 2,1∙107 Н/м;Qн – вертикальная нагрузка от колеса к рельсу 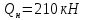 ; ;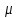 = 0,25 – коэффициент трения. = 0,25 – коэффициент трения.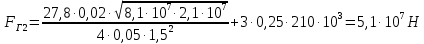 Кривые участки пути Для определения наибольшей величины боковой силы 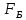 , при входе ТС в кривые участки пути, следует пользоваться формулой: , при входе ТС в кривые участки пути, следует пользоваться формулой: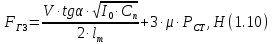 где 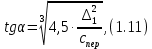 спер. = R∙ lпер.= 700*90=63000 = 65000– параметр переходной кривой; R и lпер – соответственно, радиус круговой кривой и длина переходной кривой. 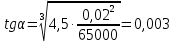 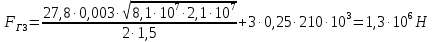 Колесная пара на прямом участке пути катится в горизонтальной плоскости по синусоидальной траектории. Длина волны при этом определяется из выражения: 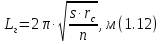 где s – половина ширины колеи, м, s = 1,520/2 = 0,760м; rc – средний радиус колеса по кругу катания, м, rc = 1,250/2 = 0,625м;  – конусность обода колеса, – конусность обода колеса,  = 0,05. = 0,05.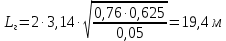 Круговая частота возмущений при извилистом движении колесной пары: 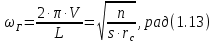 Подставляя значения в 1.13 получим: 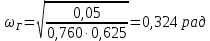 Проекции горизонтальных перемещений (на ось Y) в зависимости от времени прохождения периода колебаний описывается уравнением: 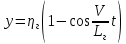 (1.14) (1.14)Скорость перемещения определяется 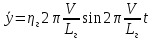 (1.15) (1.15)Ускорение горизонтальных перемещений 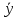 по оси Y, есть вторая производная от его перемещения по оси Y, есть вторая производная от его перемещения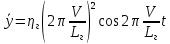 (1.16) (1.16)где 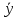 – амплитуда вынужденных колебаний кузова, м; – амплитуда вынужденных колебаний кузова, м;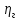 – амплитуда неровностей пути, м; – амплитуда неровностей пути, м;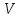 – скорость движения ТС, м/с; – скорость движения ТС, м/с;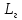 – длина периода неровностей, м. – длина периода неровностей, м.Необходимо построить графики зависимости 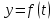 ; ; 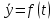 и и 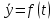 в заданном временном интервале. Проводят исследование указанных функций для различных скоростей движения ТС (10–140 км/ч). в заданном временном интервале. Проводят исследование указанных функций для различных скоростей движения ТС (10–140 км/ч).С учетом амплитуды возмущающих колебаний рассчитывают 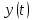 , , 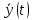 и и 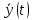 на временных участках внутри данного периода, а также величины сил инерции: на временных участках внутри данного периода, а также величины сил инерции: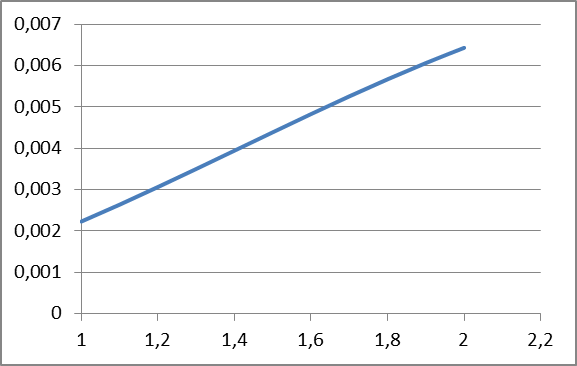 Рисунок 1.4 – Горизонтальное перемещение 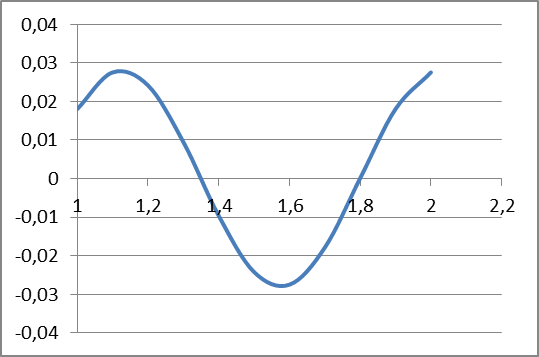 Рисунок 1.5 – Горизонтальная скорость  Рисунок 1.6 – Горизонтальное ускорение 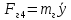 (1.17) (1.17)где 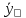 – вертикальное ускорение; – вертикальное ускорение;mГ = 23,78/2 = 11,89 т = 11890 кг 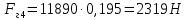 Исследуют влияние скорости ТС на величину силы инерции Сумму сил, действующих на неподрессоренную массу, приходящуюся на колесо, определяют 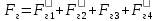 (1.18) (1.18)где 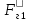 – сила удара неподрессоренной массы по крестовине, Н; – сила удара неподрессоренной массы по крестовине, Н;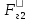 – боковая сила, возникающая при извилистом движении; – боковая сила, возникающая при извилистом движении;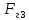 – инерционная сила, развиваемая при горизонтальных гармонических колебаниях необрессоренной массы, представляется как – инерционная сила, развиваемая при горизонтальных гармонических колебаниях необрессоренной массы, представляется как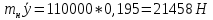 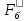 – величина боковой силы при входе ТС в кривой участок пути. – величина боковой силы при входе ТС в кривой участок пути.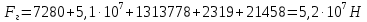 В точке контакта колеса и рельса действуют разнонаправленные силы ( 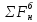 и и 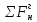 ), равнодействующая которых способствует сходу ТС с рельсов. ), равнодействующая которых способствует сходу ТС с рельсов.Устойчивость колес против схода с рельсов Чтобы гребень колеса скользил вниз по головке рельса, то есть колесо не вкатывалось на головку рельса, необходимо соблюдение условия 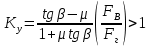 (1.19) (1.19)где 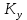 – коэффициент запаса устойчивости колеса против схода с рельса; – коэффициент запаса устойчивости колеса против схода с рельса;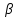 – угол наклона гребня колеса к горизонтали (60–67 °); – угол наклона гребня колеса к горизонтали (60–67 °);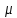 – коэффициент трения между колесом и головкой рельса (0,28); – коэффициент трения между колесом и головкой рельса (0,28);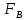 и и 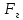 – вертикальные и горизонтальные силы, действующие на колесо, Н; – вертикальные и горизонтальные силы, действующие на колесо, Н;
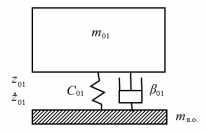
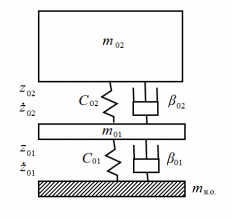
В случае потери устойчивости, колесо вкатится на головку рельса за время, с: 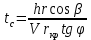 (1.20) (1.20)где 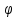 – угол набегания колеса на рельс (0,5–0,6 °); – угол набегания колеса на рельс (0,5–0,6 °);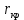 – критический радиус катания колеса по головке рельса (для локомотива – 0,635 м, для вагона – 0,485 м); – критический радиус катания колеса по головке рельса (для локомотива – 0,635 м, для вагона – 0,485 м);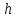 – длина гребня бандажа (0,013–0,015 м); – длина гребня бандажа (0,013–0,015 м);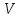 – скорость ТС, м/с. – скорость ТС, м/с.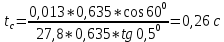 Путь схода колеса с рельса составит, м: 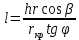 (1.21) (1.21)где 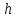 –длина гребня бандажа (0,013–0,015 м). –длина гребня бандажа (0,013–0,015 м).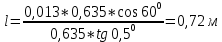 Динамическая сила, приходящаяся на колесо, передается на путь и упругий элемент, деформирующий последний. Величина этой деформации определяется, м: 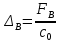 (1.22) (1.22)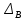 – величина деформации эквивалентного упругого элемента под действием динамической силы в вертикальной плоскости. – величина деформации эквивалентного упругого элемента под действием динамической силы в вертикальной плоскости.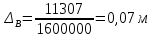 2. Динамика в системе необрессоренная – обрессоренная масса Частотная характеристика собственных вертикальных колебаний обрессоренной массы обусловлена действием динамических сил от необрессоренной массы, воздействующих на упругий элемент. Круговая частота собственных колебаний подпрыгивания обрессоренной массы определяется по следующим формулам: 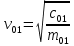 , рад/с (2.1) , рад/с (2.1)где 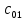 – жесткость рессорного комплекта обрессоренной массы тележки, приходящейся на одно колесо. – жесткость рессорного комплекта обрессоренной массы тележки, приходящейся на одно колесо.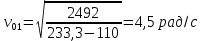 Период колебаний 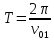 , с (2.2) , с (2.2)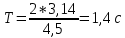 Вертикальные колебания в системе «необрессоренна масса – упругий элемент – обрессоренная масса» характеризуются перемещениями вдоль вертикальной оси. При этом учитывают частоту возмущений, реализуемых при взаимодействии необрессоренных масс и частоту колебаний обрессоренной массы. Зависимость величины вертикальных перемещений ( 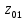 ), как функция времени описывается уравнением ), как функция времени описывается уравнением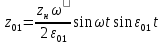 (2.3) (2.3)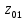 – максимальное значение вертикальных перемещений необрессоренной массы. – максимальное значение вертикальных перемещений необрессоренной массы.При этом 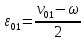 (2.4) (2.4)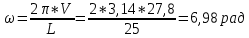 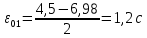 Скорость вертикальных перемещений: 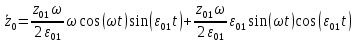 (2.5) (2.5)Ускорение вертикальных перемещений 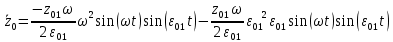 (2.6) (2.6)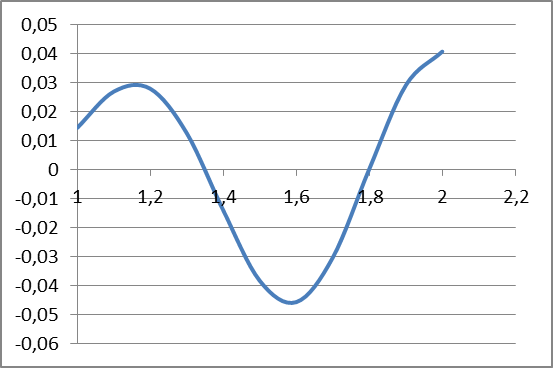 Рисунок 2.1 - Вертикальные колебания вдоль вертикальной оси 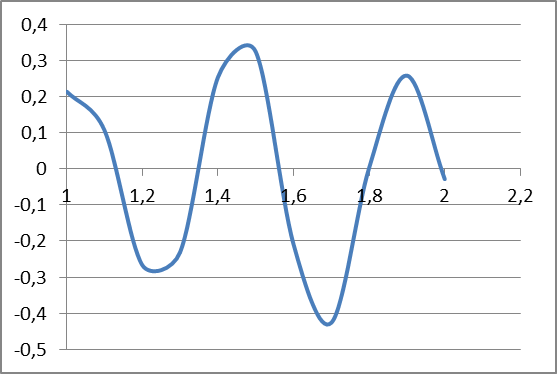 Рисунок 2.2 - Скорость вертикальных перемещений 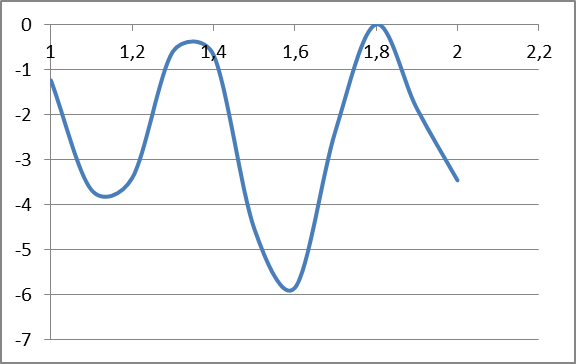 Рисунок 2.3 - Ускорение вертикальных перемещений С учетом величины максимального ускорения вертикальных перемещений, приходящейся на одно колесо и эквивалентной жесткости рессорного комплекта, приходящейся на одно колесо, определяют величину динамической силы, действующей в вертикальной плоскости вниз на упругий элемент; вверх на второй упругий элемент (рисунок 2) 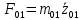 , Н (2.7) , Н (2.7)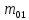 – обрессоренная масса, приходящаяся на одно колесо; – обрессоренная масса, приходящаяся на одно колесо;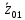 – ускорение в вертикальной плоскости обрессорнной массы, м/с2. – ускорение в вертикальной плоскости обрессорнной массы, м/с2.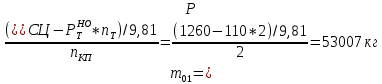 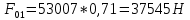 С учетом эквивалентной жесткости упругого элемента 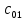 находят величину деформации упругого элемента вследствие действия динамической силы: находят величину деформации упругого элемента вследствие действия динамической силы: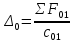 (2.8) (2.8)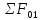 – сумма сил, действующих на упругий элемент снизу вверх и сверху вниз. – сумма сил, действующих на упругий элемент снизу вверх и сверху вниз.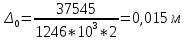 Отношение 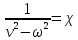 называется коэффициентом нарастания колебаний. Особенно он проявляется в условиях биения и резонанса. называется коэффициентом нарастания колебаний. Особенно он проявляется в условиях биения и резонанса.В условиях биения и резонанса колебательный процесс характеризуется переменной амплитудой, равной 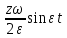 . .По мере увеличения скорости транспортного средства, 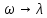 . При резонансе за каждый период колебаний амплитуда возрастает на величину . При резонансе за каждый период колебаний амплитуда возрастает на величину 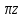 . .В указанных условиях величина вертикальных перемещений в зависимости от времени представляется выражением 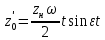 , (2.9) , (2.9)где 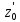 – величина вертикальных перемещений обрессоренной массы в зависимости от времени; – величина вертикальных перемещений обрессоренной массы в зависимости от времени;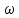 – частота вынужденных колебаний необрессоренной массы для различной скорости движения транспортного средства, рад/с; – частота вынужденных колебаний необрессоренной массы для различной скорости движения транспортного средства, рад/с;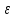 – разность частот необрессоренной и обрессоренной масс, зависящая от скорости транспортного средства, с; – разность частот необрессоренной и обрессоренной масс, зависящая от скорости транспортного средства, с;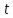 – продолжительность в рамках периода, когда меняется скорость транспортного средства. В условиях резонанса – продолжительность в рамках периода, когда меняется скорость транспортного средства. В условиях резонанса 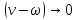 . .Исследуются ситуации при различных 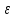 и, соответственно, различных и, соответственно, различных 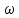 и строятся зависимости (графики) и строятся зависимости (графики) 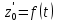 . .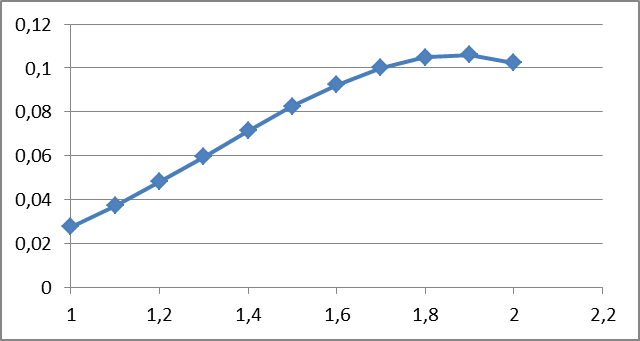 Рисунок 2.4 - Зависимость 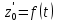 Определяется величина критической скорости: 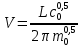 (2.10) (2.10)где 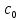 – эквивалентная жесткость рессорного комплекта, приходящаяся на одно колесо, Н/м; – эквивалентная жесткость рессорного комплекта, приходящаяся на одно колесо, Н/м;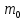 – обрессоренная масса, приходящаяся на одно колесо; – обрессоренная масса, приходящаяся на одно колесо;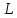 – длина волны неровности. – длина волны неровности.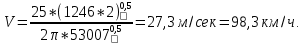 3 Динамика в системе обрессоренная – обрессоренная массы Основные исходные данные: - обрессоренная масса тележки ( 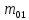 ); );- обрессоренная масса кузова ( 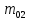 ); );- жесткость рессорного комплекта между обрессоренными массами ( 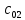 ), приходящаяся на рессорный комплект центрального подвешивания, Н/м. ), приходящаяся на рессорный комплект центрального подвешивания, Н/м.Частотная характеристика обрессоренной массы 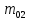 определяется из выражения: определяется из выражения: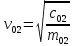 , рад/с (3.1) , рад/с (3.1)где 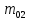 – обрессоренная масса, приходящаяся на один рессорный комплект, кг. – обрессоренная масса, приходящаяся на один рессорный комплект, кг.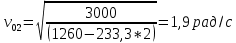 Период колебаний, соответствующих данной частоте: 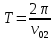 , с (3.2) , с (3.2)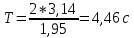 В результате сравнения величин частот собственных колебаний, находят 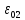 : :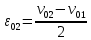 (3.3) (3.3)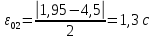 Воспользовавшись уравнениями, находят зависимости величины вертикальных перемещений, скорости и ускорения 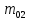 : :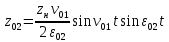 (3.4) (3.4)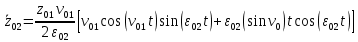 (3.5) (3.5)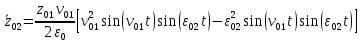 (3.6) (3.6)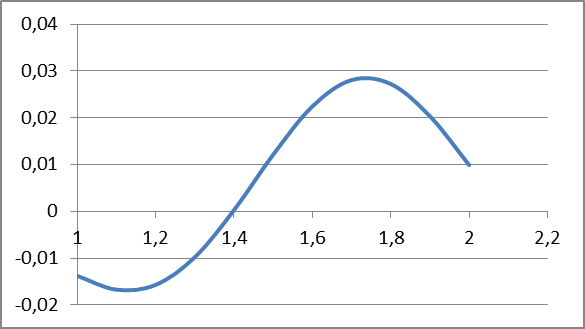 Рисунок 3.1 - Величина вертикальных перемещений 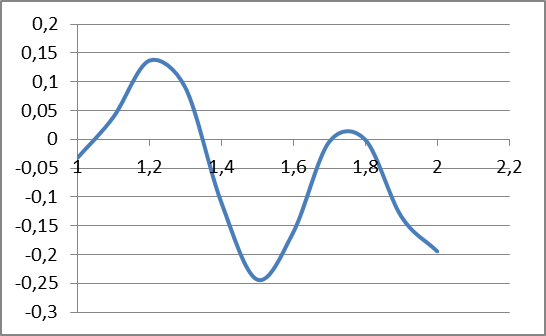 Рисунок 3.2 – Величина вертикальной скорости 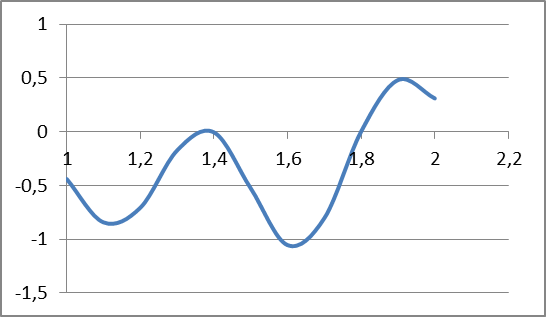 Рисунок 3.3 – Величина вертикального ускорения Величина динамической силы, действующих в системе двух обрессоренных масс, определяется: 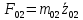 (3.7) (3.7)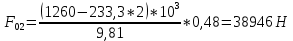 С учетом эквивалентной жесткости комплекта упругих элементов, представленном в рессорном комплекте, находят величину деформации его при воздействии динамической силы и силы тяжести 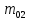 . .
Полная деформация упругого элемента с жесткостью 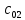 , определится с учетом динамической силы, действующей вертикально вверх, передаваемой от массы , определится с учетом динамической силы, действующей вертикально вверх, передаваемой от массы 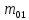 , т.е.: , т.е.: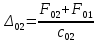 (3.8) (3.8)где 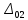 – сжатие упругого элемента с жесткостью – сжатие упругого элемента с жесткостью 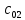 . .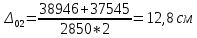 Галопирование обрессоренной массы 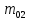 характеризуется вертикальными перемещениями относительно оси OY в соответствии со схемой, приведенной на рисунке 2. характеризуется вертикальными перемещениями относительно оси OY в соответствии со схемой, приведенной на рисунке 2.Круговая частота собственных колебаний галопирования кузова: 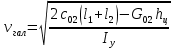 , рад/с (3.9) , рад/с (3.9)где 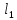 – половина базы по осям рессорных комплектов; – половина базы по осям рессорных комплектов;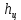 – высота центра тяжести кузова транспортного средства над уровнем рессорного подвешивания; – высота центра тяжести кузова транспортного средства над уровнем рессорного подвешивания;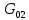 – вес кузова ТС; – вес кузова ТС;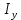 – момент инерции транспортного средства, кг·м2. – момент инерции транспортного средства, кг·м2.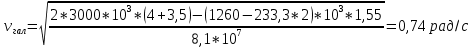 Период колебаний 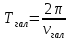 (3.10) (3.10)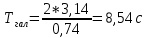 Учитывая, что в период галопирования рессорные комплекты нагружены по-разному: передние по ходу движения могут быть разгружены в противоположность вторым, которые нагружаются весьма существенно. Угол качания ( 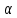 ) относительно горизонтальной плоскости может составить 0,7–1,5 ° ) относительно горизонтальной плоскости может составить 0,7–1,5 °Критическое отклонение кузова между осями упругих элементов может быть определено из выражения: 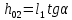 (3.11) (3.11)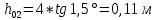 Используя уравнение гармонических колебаний для вертикальных перемещений: 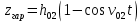 , (3.12) , (3.12)а также уравнения для скорости и ускорения вертикальных перемещений во временном отрезке, соответствующем периоду колебаний. С учетом найденной величины максимального ускорения, определяют динамическую силу, развиваемую при галопировании, принимая массу, действующую на задние упругие элементы, 0,75 от массы кузова. Боковая качка обрессоренной массы 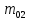 в условиях, когда спровоцированы гармонические колебания с круговой частотой собственных колебаний кузова относительно оси ОХ, определяемая: в условиях, когда спровоцированы гармонические колебания с круговой частотой собственных колебаний кузова относительно оси ОХ, определяемая: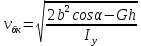 , рад/с (3.13) , рад/с (3.13)где 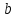 = 2,036 м– расстояние между серединами шеек букс; = 2,036 м– расстояние между серединами шеек букс;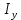 – момент инерции кузова ТС относительно оси ОY, кг·м2. – момент инерции кузова ТС относительно оси ОY, кг·м2.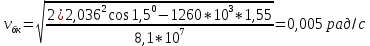 Такие расчеты могут быть выполнены, если известна амплитуда вынужденных колебаний боковой качки, которую находят с учетом критических углов наклона кузова по оси ОХ. Если 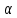 будет составлять 0,7–1,2 °, то уравнение будет иметь вид: будет составлять 0,7–1,2 °, то уравнение будет иметь вид: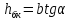 (3.15) (3.15)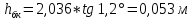 Аналогично вышеприведенному оценивают вертикальную динамическую силу, действующую на упругие элементы (2 боковых рессорных комплекта) при боковой качке. Величины проекций сил ( 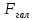 и и 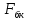 ) на ось OZ учитывают при оценке их действия на упругие элементы. ) на ось OZ учитывают при оценке их действия на упругие элементы.4 Гасители колебаний Уравнение сил, действующих в диссипативной системе Уравнение сил с учетом принципа Даламбера, имеет следующий вид (рисунок 3): 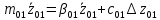 (4.1) (4.1)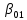 – коэффициент сопротивления гасителя, Н·с/м; – коэффициент сопротивления гасителя, Н·с/м;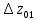 – деформация, обусловливающая действие динамических сил, м; – деформация, обусловливающая действие динамических сил, м;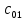 – жесткость упругого элемента, Н/м; – жесткость упругого элемента, Н/м;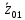 – максимальная скорость необрессоренной массы, м/с в вертикальной плоскости; – максимальная скорость необрессоренной массы, м/с в вертикальной плоскости;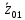 – максимальное ускорение необрессоренной массы в вертикальной плоскости, м/с2. – максимальное ускорение необрессоренной массы в вертикальной плоскости, м/с2.
Из уравнения (4.1) для одноступенчатого подвешивания, величина коэффициента сопротивления гасителя определяется: 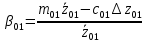 (4.2) (4.2)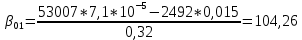 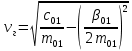 (4.3) (4.3)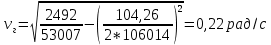 где 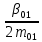 – круговая частота системы, учитывая сопротивление гасителя; – круговая частота системы, учитывая сопротивление гасителя;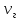 – круговая собственная частота обрессоренной массы – круговая собственная частота обрессоренной массы 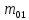 в присутствии гасителя, рад/с. в присутствии гасителя, рад/с.Функция вертикальных перемещений от времени в рамках одного периода: 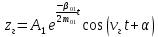 (4.4) (4.4)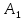 = 0,086 м – амплитуда вынужденных колебаний обрессоренной массы ( = 0,086 м – амплитуда вынужденных колебаний обрессоренной массы (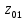 ); );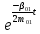 – множитель, убывающий с возрастанием времени. – множитель, убывающий с возрастанием времени.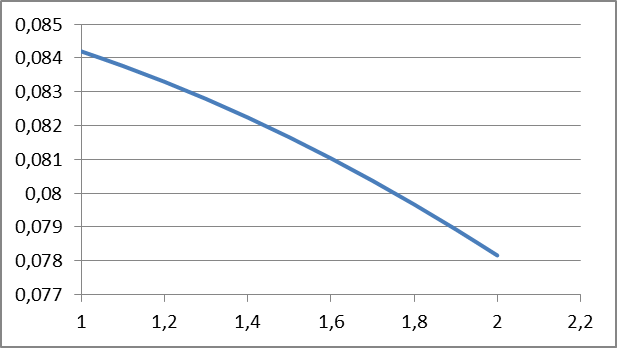 Аналогичные расчеты для гасителя колебаний второй ступени подвешивания (рисунок 4).
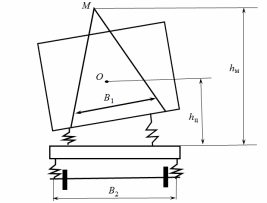
С уменьшением максимальной амплитуды колебаний, уменьшается ускорение вертикальных перемещений 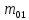 , и, соответственно, уменьшается величина динамической силы. , и, соответственно, уменьшается величина динамической силы.Устойчивость кузова на рессорах Устойчивость кузова на рессорах определяется неравенством (рисунок 5): 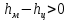 (4.8) (4.8)где 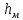 – высота метацентра (метацентр – центр кривизны, траектории который перемещается при наклонении транспортного средства). Метацентр определяется пересечением осевых линий центрального рессорного подвешивания ТС, рассчитываемая по формуле: – высота метацентра (метацентр – центр кривизны, траектории который перемещается при наклонении транспортного средства). Метацентр определяется пересечением осевых линий центрального рессорного подвешивания ТС, рассчитываемая по формуле:
Данное условие является критерием устойчивости. Оно ограничивает применение чрезвычайно гибких рессор, т.е. суммарный статический прогиб всего подвешивания 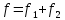 (4.9) (4.9)где 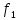 – статический прогиб буксового подвешивания; – статический прогиб буксового подвешивания;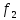 – статический прогиб центрального подвешивания. – статический прогиб центрального подвешивания.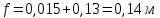 | ||||||||||||||||||||


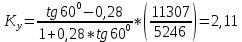
 1
1