Множественная линейная регрессия. Мн.линейная регрессия. Исходные данные для анализа
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Целью исследования являлось изучение влияния набранных очков, передачи мяча, подборов на итоговый рейтинг баскетболистов. Занесем в Excel исходные данные (Таблица 1). Таблица 1 – Исходные данные для анализа
Для начала проведем анализ регрессии методом наименьших квадратов, где рейтинг баскетболиста будет служить зависимой переменной. С помощью вкладки «Анализ данных»-«Регрессия» построим модель регрессии. (Рисунок 1) 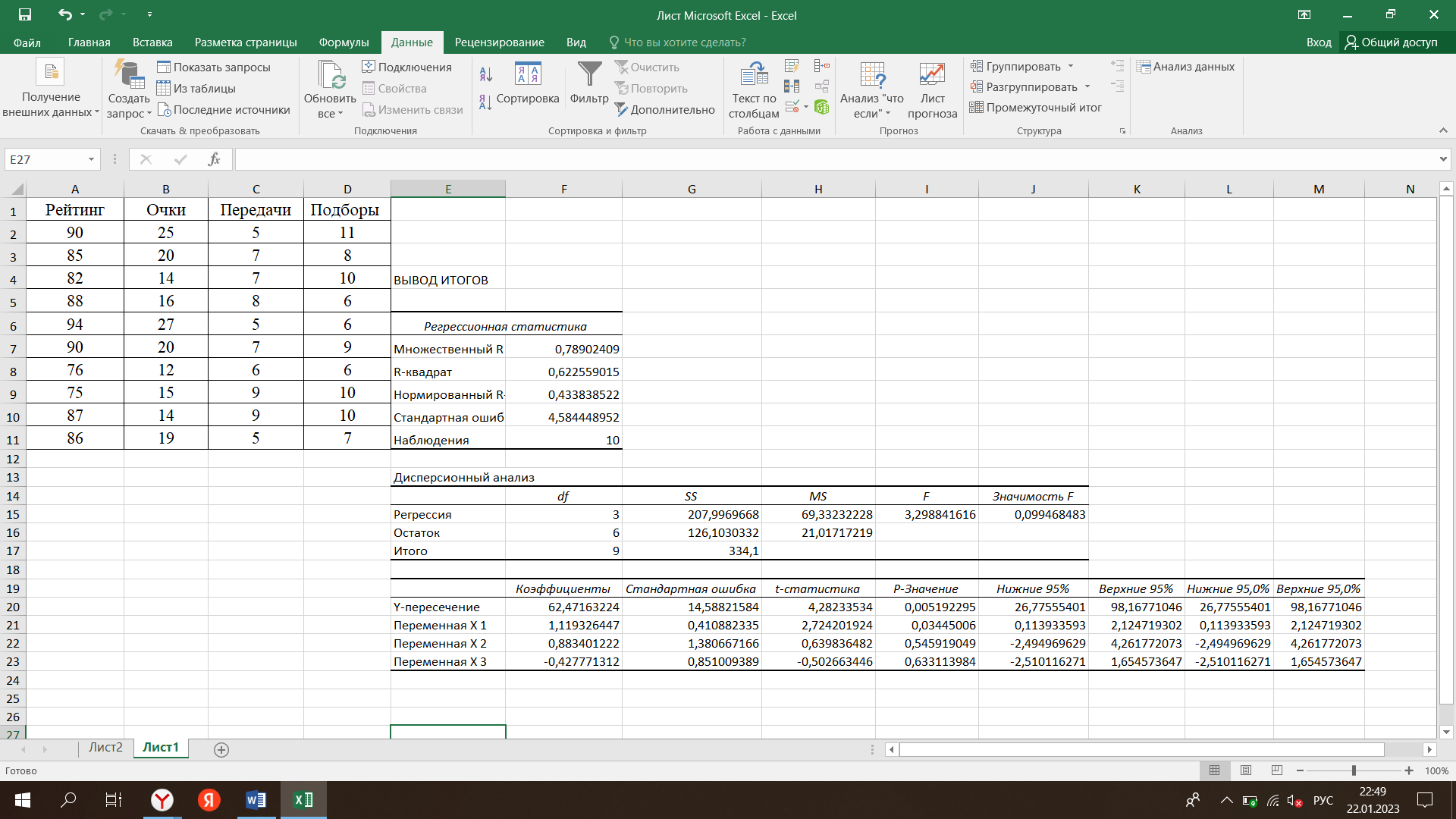 Рисунок 1 - Построение модели регрессии на основе исходных данных Отсюда мы видим, что на основании данных t-статистики и p-значений, у нас есть один значимый фактор – количество очков, однако стоит перепроверить данную теорию с помощью теоремы Гаусса-Маркова( У = а0 + u). Теперь мы можем рассчитать VIF для каждой их независимых переменных (очки, передачи, подборы). Для этого рассчитаем по формуле: VIF = 1/(1-R-квадрат) (рисунок 2) 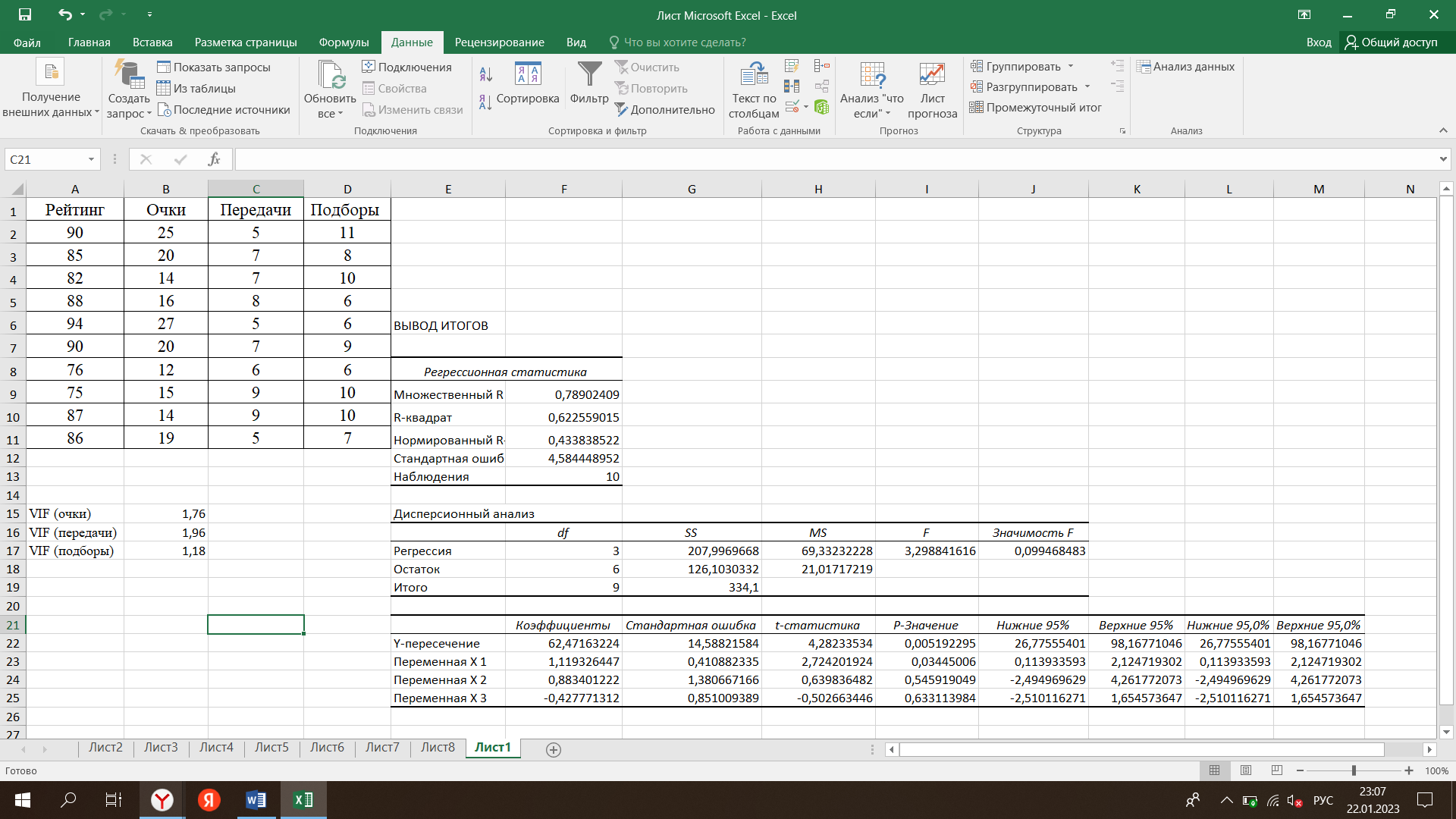 Рисунок 2 – Расчет значений VIF для всех независимых переменных Отсюда следует вывод, что значения VIF для всех независимых переменных в нашей регрессионной модели близко к 1, мультиколллениарность в нашем случае незначительная. Далее с помощью «Анализ данных» - «Корреляция» построим матрицу для исключения тех переменных, которые высоко коррелированы. Получим следующие данные (рисунок 3) 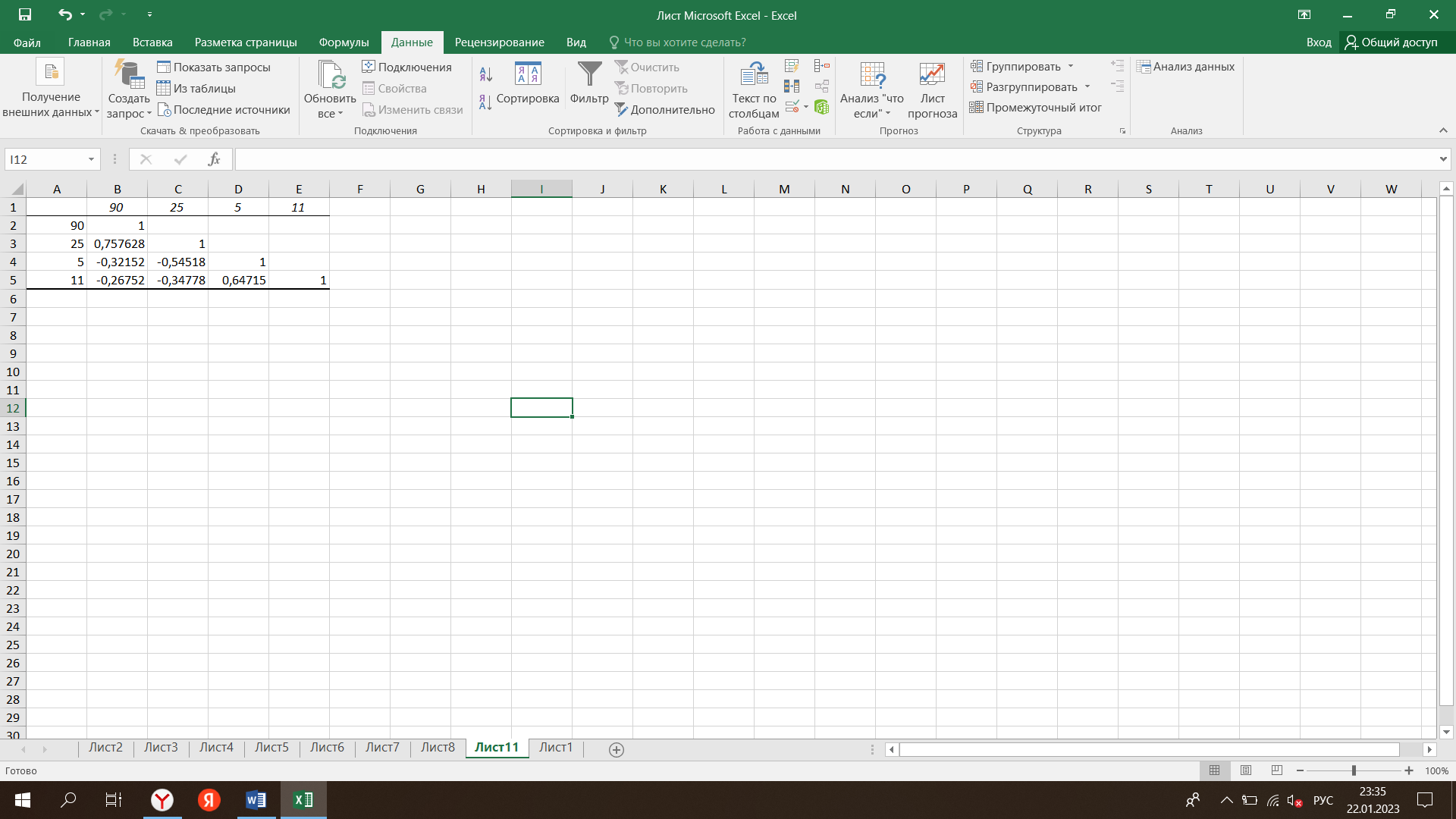 Рисунок 3 – Результаты построения корреляционной матрицы В нашем случае положительную корреляцию имеет показатель набранных очков. Проведем снова анализ VIF (рисунок 4) 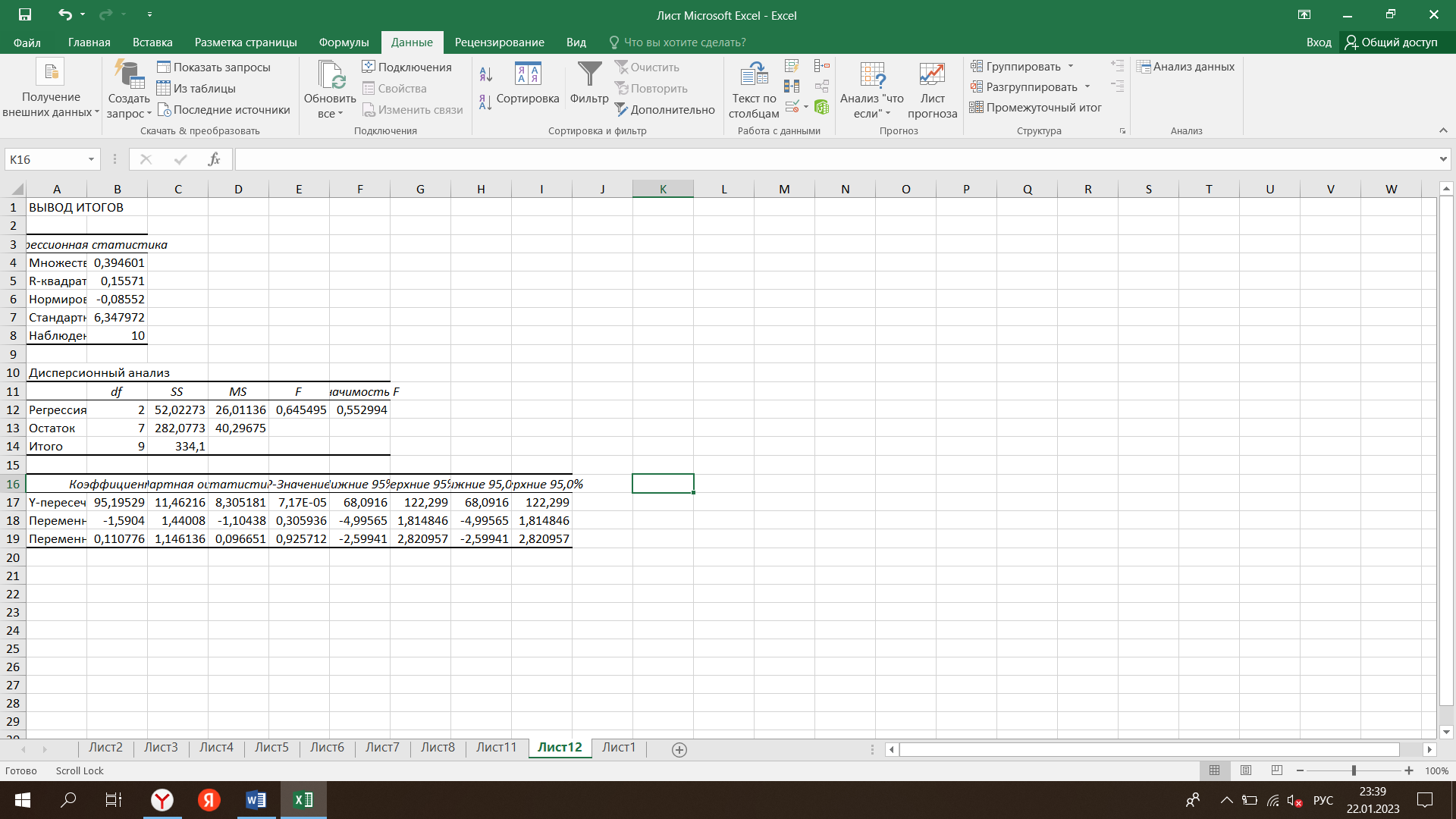 Рисунок 4 – VIF – анализ после исключения переменной «очки» Тогда зависимость рейтинга от передачи и подборов будет составлять: 1,1844 и 0,0844 соответственно. Отсюда делаем вывод, что меньше всего влияние на рейтинг оказывает количество подборов. |
