Курсовая работа Цифровая обработка сигналов. Курсовая_цифровая обр сигналов_Абильмажинов_2 вар. Исходные данные к расчётам Вид модуляции офм
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
 получаем двоичные коды. Для построения кодов с проверкой на чётность необходимо добавить к кодовым комбинациям по одной позиции и заполнить её символом 0 или 1 по правилу чётности числа единиц. получаем двоичные коды. Для построения кодов с проверкой на чётность необходимо добавить к кодовым комбинациям по одной позиции и заполнить её символом 0 или 1 по правилу чётности числа единиц. 3 Помехоустойчивое кодирование с проверкой на чётность. Это систематический код (k+1,k) – код, в котором операция кодирования и декодирования сигнала проводится как проверка на четность. Кодовое расстояние для этого кода d0=2. При этом код всегда обнаруживает однократные ошибки. Разрешенная комбинация этого кода при любом числе информационных символов имеет всегда один проверочный. Размещение проверочного символа в коде не имеет значения. Обычно его ставят в конце после информационных. Значение проверочного символа в разряде выбирается из условия, что общее число единиц в образованной таким образом разрешенной кодовой комбинацией было бы четным, то есть сумма по модулю для всех символов кодовой комбинации равнялась нулю. Если разряды кодовых комбинаций пронумеровать справа налево и символы в этих разрядах обозначить для безызбыточного кода а1, а2…аk, а для корректирующего b1, b2…bk+1, то описанная выше процедура формирования кодовой комбинации запишется в виде. 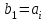 , при i=1,2,…k , при i=1,2,…k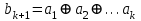 Причем 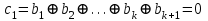 Первое равенство означает, что информационные символы при кодировании не изменяются, второе описывает правило формирования проверочного символа и определяет контрольную сумму этого кода как результат проверки кодовой комбинации на четность. При любой однократной ошибке передачи последнее условие нарушается и тем самым выявляется ошибка. Простейшим примером кода с проверкой на четность является код Бодо, в котором к пятизначным комбинациям информационных символов добавляется шестой контрольный символ: 11001,1, 10011, 0. Правило вычисления контрольного символа находится так: 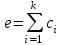 Откуда вытекает, что для любой комбинации и сумма всех символов по модулю 2 будет равна нулю. Структурная схема устройства с проверкой на четность приведена на рисунке 3.1: 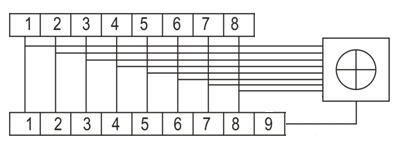 Рисунок 3.1 Структурная схема кодера с проверкой на четность Математическое описание работы кодера:  Нарушение четности имеет место при появлении однократных, трех кратных и в общем случае нечетной кратности , что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы, поэтому такие ошибки не обнаруживаются. 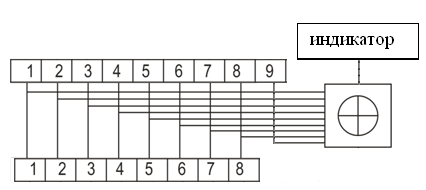 Рисунок 3.1 Структурная схема декодера кода с проверкой на четность Анализ. Первое равенство означает‚ что информационные символы при кодировании не изменяются‚ второе описывает правило формирования проверочного символа и определяет контрольную сумму этого кода как результат проверки кодовой комбинации на четность. При любой однократной ошибке передачи последнее условие нарушается и тем самым выявляется ошибка 4.1 Определение длительности одиночного элемента кодовой комбинации ИКМ с проверкой на чётность Для определения длительности одиночного элемента кодовой комбинации ИКМ сигнала (тактового интервала Тmax) с проверкой на четность необходимо последовательно определить: a) Количество информационных элементов К кодовой комбинации. б) общую длину кодовой комбинации n с учетом кодирования с проверкой не четность. Следует считать, что общая длительность кодовой комбинации равна интервалу дискретизации Тд, определенному по теореме Котельникова с учетом необходимого защитного частотного интервала 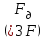 . . А так как ∆F=5,0 кГц, а Fд>2∆F=5 кГц и учитывая то, выбираем подходящую частоту Fд=6 кГц. Длина кодовой комбинации с учётом проверки на чётность будет равна: 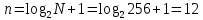 Следовательно, длительность импульса: 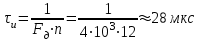  4.2 Характеристики источника независимых двоичных сообщений Вероятность появления символа «1» p(1)=0,001+0,46=0,461 Следовательно, вероятность появления символа «0» p(0)=1-p(1)=0,539 Энтропия источника определяется распределением вероятностей выбора элементарных сообщений из общей совокупности. Обычно отмечают, что энтропия характеризует источник с точки зрения неопределённости выбора того или иного сообщения. Энтропия всегда величина вещественная, ограниченная и не отрицательная: 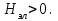 Для двоичного источника информации максимальная энтропия: 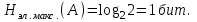 Энтропия характеризует среднее количество информации, содержащейся в сообщении. Энтропия является основной характеристикой источника, чем она выше, тем труднее передать сообщение по каналу связи. Необходимая затрата энергии на передачу сообщения пропорциональна его энтропии. Для вычисления энтропии сигнала применим следующую формулу: 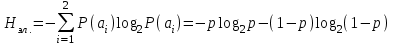 Используя формулу, получаем: 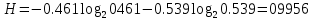 Производительность источника (скорость создания на выходе информации квантующего устройства) представляет собой суммарную энтропию сообщений, переданных за единицу времени и рассчитывается по формуле : 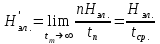 где tcp=tH/n=Tтакт – средняя длительность сообщения, следовательно, 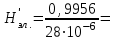 39824 (бит/с) 39824 (бит/с)Избыточность источника сообщения - показывает, какая доля максимально возможной энтропии не используется источником и оценивается коэффициентом избыточности: 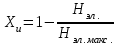 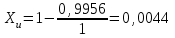 Избыточность составляет 0,4%. 4.3 Определение величины h2 Необходимо определить величину параметра – отношение сигнал/шум на входе детектора, при которой достигается вероятность ошибки Рош=3·10-6, если помеху, воздействующую на сигнал считать белым шумом со спектральной плотностью мощности G0=10-5 В2/Гц. В общем случае вероятность ошибки для ОФм сигнала определяется следующим выражением: 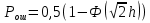 Функция Крампа Ф (h) выражается через интегральную зависимость: 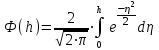 Подставив Функцию Крампа в формулу вероятности ошибки, получим: 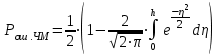 Используя уравнение, с учетом того, что мы имеем известную вероятность ошибки, и подставив ее значение, можем найти h: 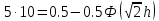 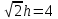 h=5.657 Тогда отношение сигнал / шум будетравен: h2=32,0015 4.4 Теорема Шеннона для пропускной способности канала связи Формулировка теоремы Шеннона для дискретного канала: если производительность источника Нист(А), меньше пропускной способности канала С‚ т.е. Нист(А)<С‚ то существует способ кодирования (преобразования сообщения в сигнал на входе) и детектирования (преобразования сигнала в сообщение на выходе канала)‚ при котором вероятность ошибочного декодирования может быть сколь угодно мала. Если же Нист(А)≥С‚ то таких способов не существует. Пропускная способность для непрерывного, без памяти, канала связи с аддитивным белым шумом: 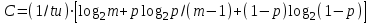 где m – количество дискретных сигналов‚ р – вероятность ошибки сигнала в канале‚ tи – длительность единичного импульса сигнала. Подставляя исходные данные в формулу пропускной способности канала связи‚ получаем: 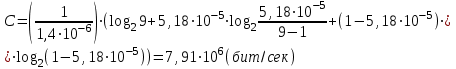 Так как выполняется условие Нист(А) При увеличении полосы частот канала ΔFк‚ пропускная способность канала стремится к пределу: 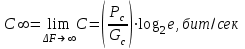 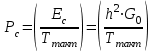 тогда: 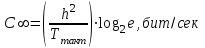 из этой формулы следует‚ что потенциальная пропускная способность равна 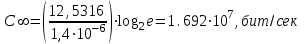 Вывод: Столь большая разница между производительностью источника Нист(А) в целом предопределяет низкую эффективность системы связи и подтверждает неравенство шеннона: Нист(А) 5 Разработать алгоритм и соответствующую структурную схему дискретно-аналогового модулятора Модуляция - это медленное изменение во времени значений, каких либо параметров несущего колебания амплитуды, частоты или фазы. Значения модуляции параметров на интервале времени, равном периоду несущего колебания, при этом практически не изменяются. Модулированное радиочастотное колебание называют часто радиосигналом. В соответствии с вариантом выбирается вид модуляции. В данной курсовой работе будет использоваться ОФМ модуляция. На рисунке 5.1 представлена функциональная схема ОФМ-модулятора.   Рисунок 5.1 Функциональная схема модулятора Математическое описание:  где 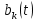 - кодовая комбинация; - кодовая комбинация; 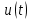 - модулированный сигнал; - модулированный сигнал;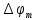 - девиация фазы. - девиация фазы.На рисунке 5.2 изображена структурная схема ОФМ-модулятора.  Кодер ОФМ 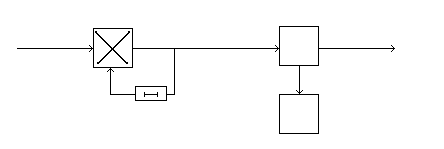 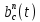 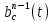 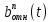 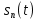 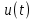 ФМ Г Рисунок 5.2 Структурная схема ОФМ-модулятора Математическое описание: 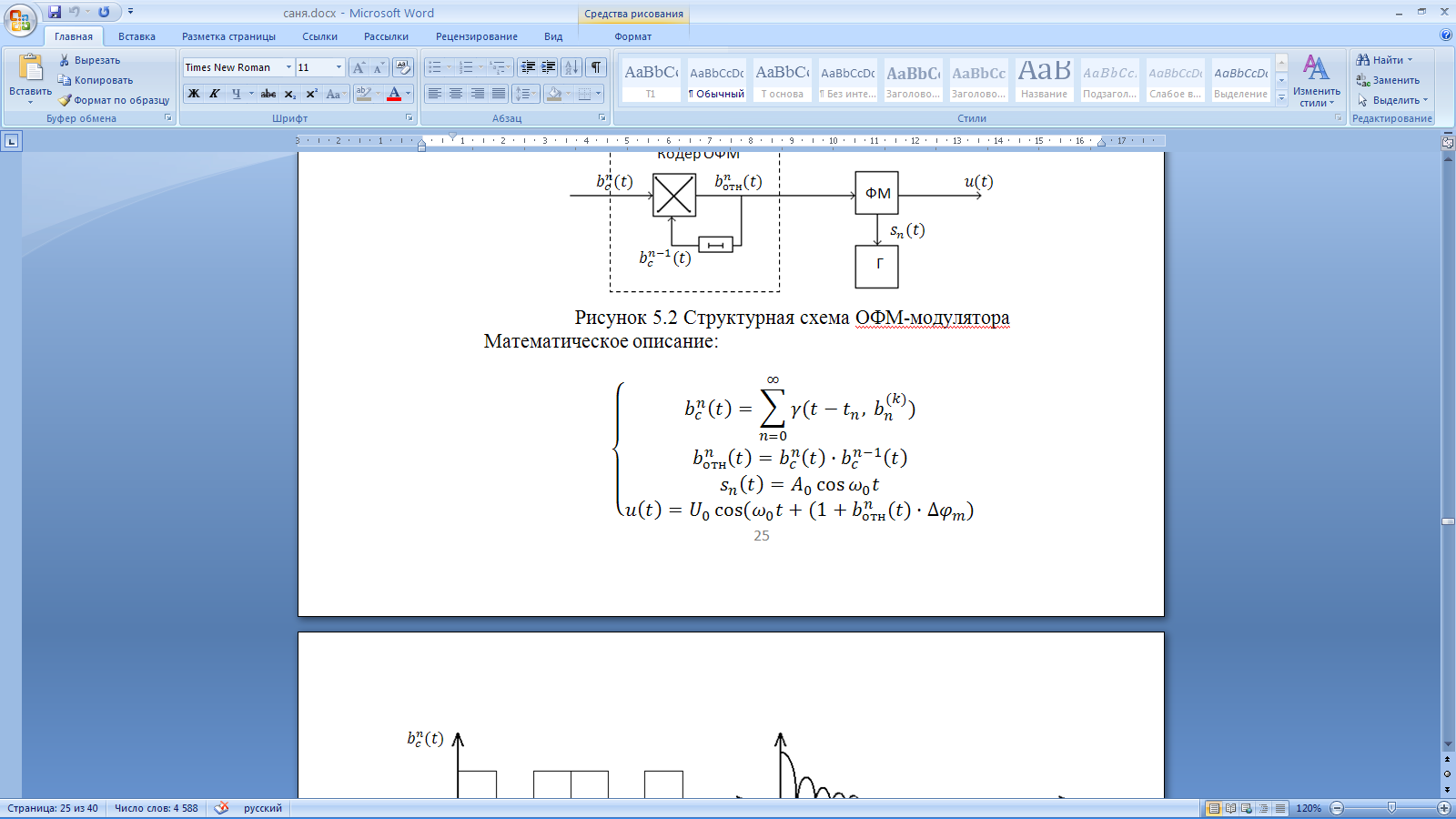 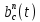 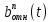 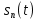 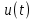 t t t t ω ω ω ω ω0 ω0
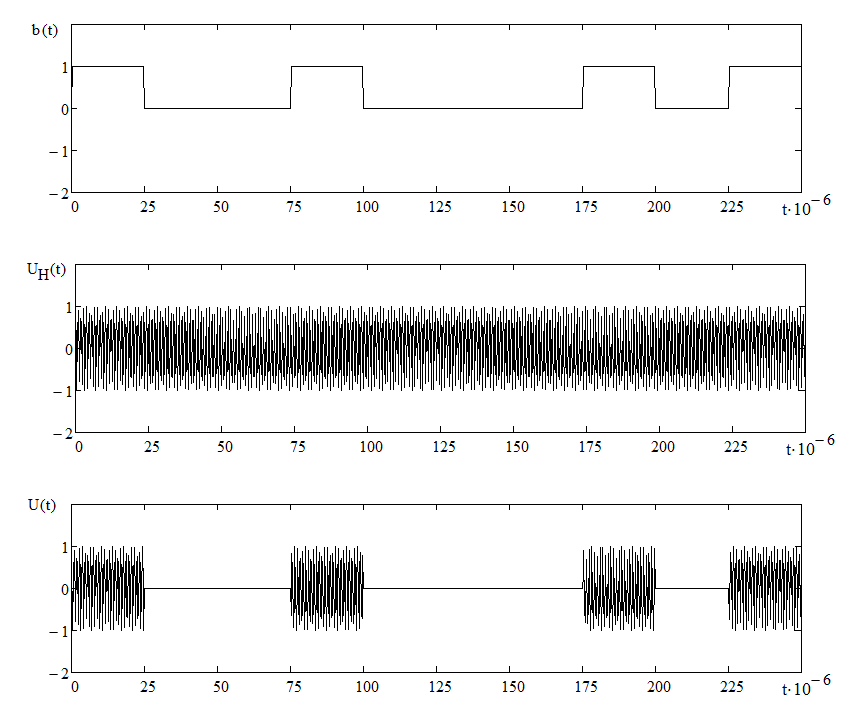
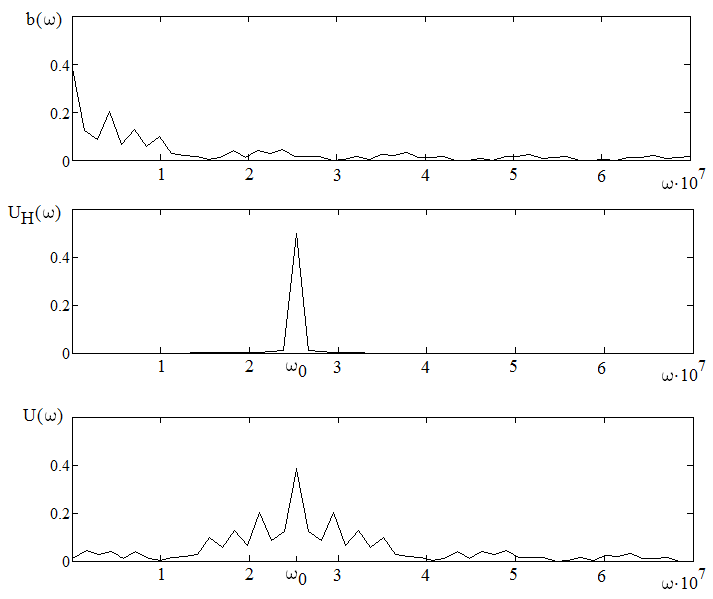
Рисунок 5.3 Формирования сигнала во временной и частотной области В результате частотной модуляции во временной области цифровой сигнал заполняется высокочастотным колебанием, что в свою очередь повышает помехоустойчивость передаваемого сообщения. Таким образом, спектр радиочастотного колебания при частотной модуляции гармоническим колебанием состоит из трех составляющих: нижней боковой, несущей и верхней боковой гармоник. Видно, что амплитуды боковых составляющих зависят от коэффициента модуляции Процесс формирования сигнала с ОФМ можно свести к случаю формирования сигнала с ФМ путём перекодирования. 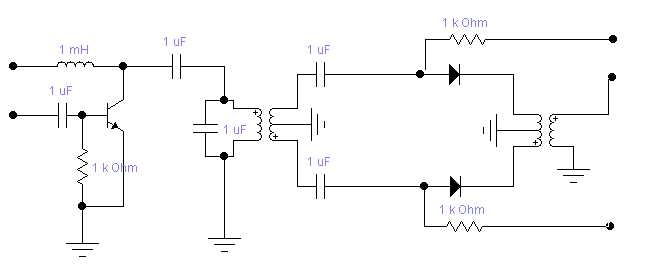 Рисунок 5.4 Принципиальная схема ОФМ модулятора Для оценки качества работы модулятора с точки зрения вносимых искажений, используют статическую модуляционную характеристику (рисунок 5.3). Для исключения нелинейных искажений необходимо использовать только линейный участок модуляционной характеристики на отрезке от Umin до Umax, но желательно обеспечить запас линейности. В этом случае не будет превышена заданная вероятность ошибки. Если линейность на заданном участке не будет обеспечена, то будет превышена допустимая вероятность ошибки Pош. Рисунок 5.5 – Модуляционная характеристика ОФМ модулятора 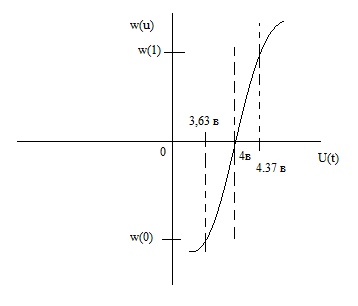 В модуляторе синхронная двоичная последовательность биполярных импульсов b(t) осуществляет модуляцию гармонического переносчика Umcos(2πf0t), (Um=1 В, f0= 100Vn, где Vn – число двоичных символов, выдаваемых кодером в единицу времени). 6 Разработать аналитический алгоритм и соответствующую структурную схему дискретно-аналогового демодулятора Постановка задачи. Заданными считаются: Характеристики источников сообщений при необходимости всех предварительных преобразующих и кодирующих устройств. Процедуры формирования модулированных сигналов, спектральные, временные характеристики сигналов. Характеристики линии связи. Статические характеристики помех. Требуется определить оптимальный алгоритм и структурные схему демодулятора (приёма и обработки сигналов) по критерию минимума ошибки. Предположим, что все искажения в канале строго детерминированы и случайным является только гауссовский аддитивный шум n(t), который вначале полагаем белым, со спектральной плотностью N0. это значит, что при передаче сигнала ui(t) (символа bi (i=0,1)) приходящий сигнал можно описать моделью: 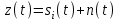 Алгоритм приема сводится к проверке одного неравенства 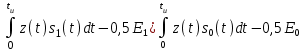 Где Ei – энергия сигнала si(t). Устройство, непосредственно вычисляющее скалярное произведение 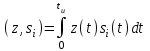 , называют активным фильтром, или коррелятором, поэтому приемник, реализующий алгоритм, называют корреляционным , называют активным фильтром, или коррелятором, поэтому приемник, реализующий алгоритм, называют корреляционным |