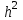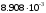Курсовая работа Цифровая обработка сигналов. Курсовая_цифровая обр сигналов_Абильмажинов_2 вар. Исходные данные к расчётам Вид модуляции офм
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
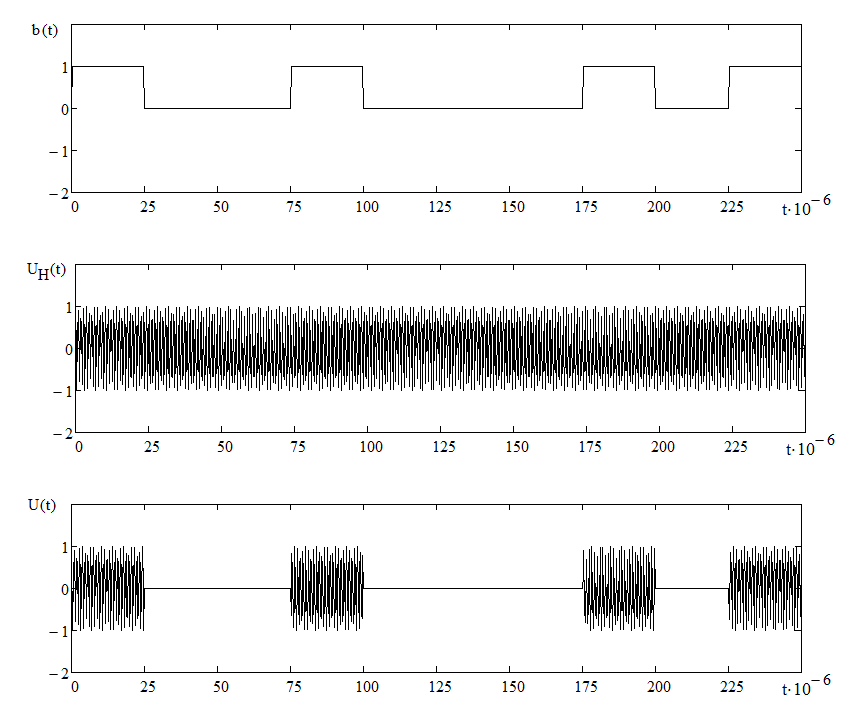
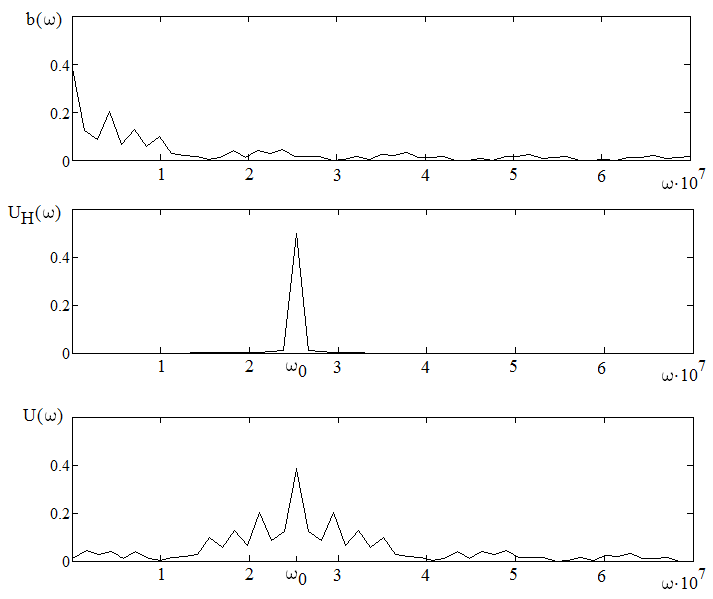
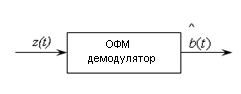 Рисунок 6.1 Функциональная схема относительного фазового демодулятора Математическое описание: 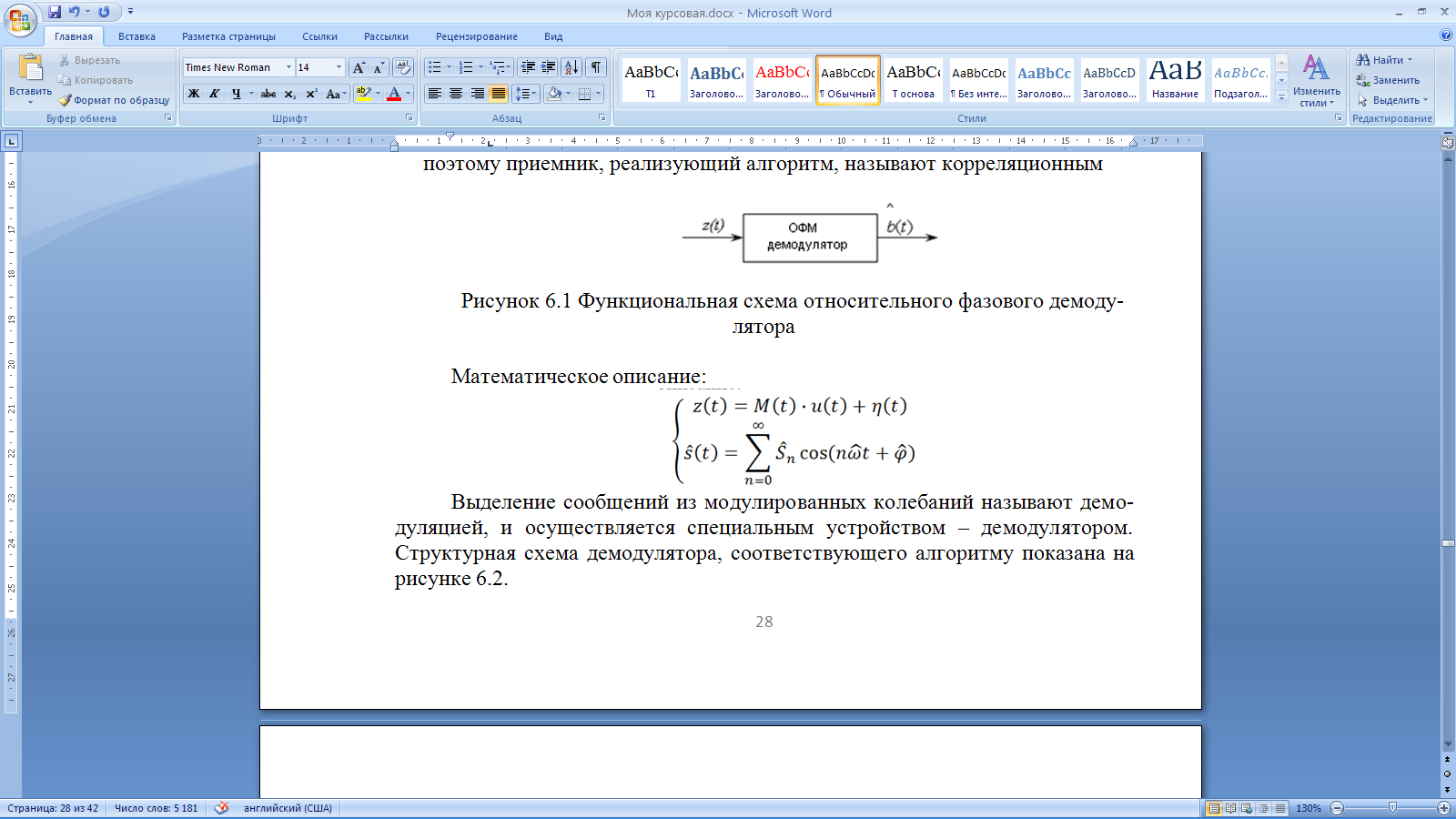 Выделение сообщений из модулированных колебаний называют демодуляцией, и осуществляется специальным устройством – демодулятором. Структурная схема демодулятора, соответствующего алгоритму показана на рисунке 6.2. 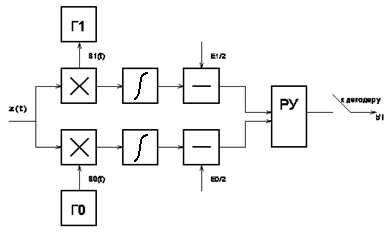 Рисунок 6.2 Оптимальный приемник при точно известных сигналах, построенный по корреляционной схеме Диаграммы сигналов при частотной модуляции.
Рисунок 6.3 ОФМ демодуляция во временной и частотной области Принципиальная схема ОФМ демодулятора изображена на рисунке 6.4 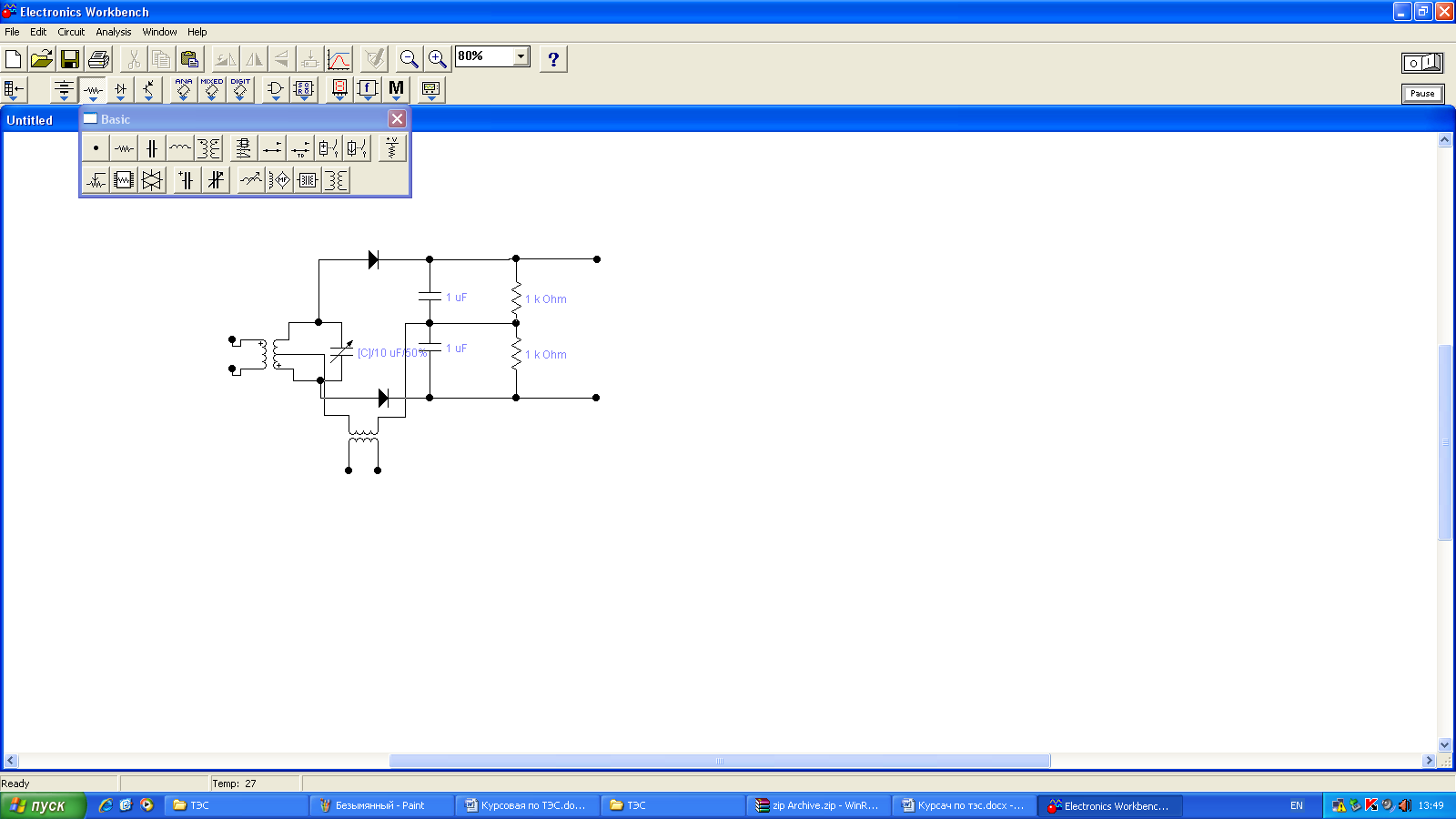 Рисунок 6.4 Принципиальная схема ОФМ демодулятора Оптимальный некогерентный прием оказывается возможным только при приеме ОФМ сигнала с большим уровнем несущей и, если коэффициент модуляции находится в пределах 0 ≤ М ≤ 1. Когда входное напряжение 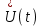 положительно, через диод протекает ток, а когда отрицательно, ток равен нулю. Ток, протекающий через диод в прямом направлении, заряжает конденсатор до некоторого напряжения, полярность которого такова, что оно стремится запереть диод. В результате открытое или запертое состояние диода в каждый момент времени определяется разностью входного напряжения положительно, через диод протекает ток, а когда отрицательно, ток равен нулю. Ток, протекающий через диод в прямом направлении, заряжает конденсатор до некоторого напряжения, полярность которого такова, что оно стремится запереть диод. В результате открытое или запертое состояние диода в каждый момент времени определяется разностью входного напряжения 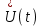 . .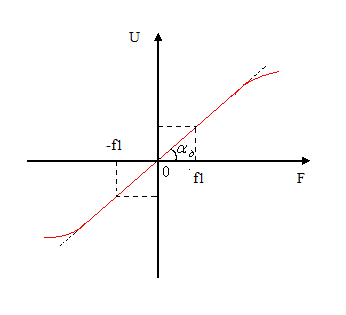 Рисунок 6.5 демодуляционная характеристика ОФМ демодулятора Чтобы в демодуляторе не возникали искажения, его демодуляционная характеристика должна быть линейной 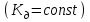 , а частотная характеристика – равномерной в пределах полосы частот, занимаемой спектром сообщения. , а частотная характеристика – равномерной в пределах полосы частот, занимаемой спектром сообщения.7 Предложить способ кодирования в аналитической, структурной, расчетно-графической формах модулятора-демодулятора, кодера-декодера, позволяющей повысить более чем на два порядка качественнее показатели систем. Так как ОФМ имеет наилучший качественный показатель по сравнению с другими видами модуляции (кроме ФМ), то для качественного увеличения помехоустойчивости системы, её следует обеспечить кодером-декодером с более совершенным кодом, наиболее совершенными кодами используемыми в современной технике являются систематические коды. К их числу относятся циклические коды предложенные независимо друг от друга Баузом, Чоудхири и Хоквингемом (БЧХ). Коды Боуза-Чоудхури-Хоквингема (БЧХ) – класс циклических кодов, исправляющих кратные ошибки, т. е. две и более (d0 5). Для улучшения помехоустойчивости предлагается использовать (15, 7) БЧХ код для этого кода минимально Хеммингово расстояние d = 7, а это значит, что подобный код может обнаружить 5 ошибок или исправлять 2 такой код существенно уменьшит вероятность ошибочного приема кодовой последовательности. Коды БЧХ строятся по заданной длине кодового слова n и числа исправляемых ошибок S , при этом количество информационных разрядов k не известно пока не выбран определяющий полином. Код БЧХ длины n, исправляющий qnc - кратные ошибки, это циклический блочный код над полем GF(p), корнями порождающего многочлена которого являются βν, βν+1, βν+2qnc-1, где β – элемент конечного поля ; ν – целое число. В соответствии с этим определением и выражением порождающий многочлен кода БЧХ может быть представлен наименьшим общим кратным g(x)= HOK[Mν(x),Mν+1(x),…, Mν+2qnc-1(x)] где Mj(x) – минимальные многочлены элементов βj . 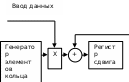 Рисунок 7.1Функциональная схема БЧХ кодера Данный кодер отличает то полезное свойство, что он не требует битовых операций и обеспечивает легкую смену кодового полинома. В силу этих обстоятельств легко выполняется как аппаратная, так и программная реализация такого кодера для БЧХ кода. Математическое описание 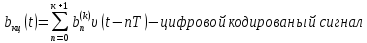 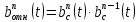 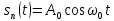 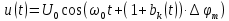 - сигнал ОФМ - сигнал ОФМЗадача приемника заключается в следующем: он анализирует смесь сигнала и шума Z(t) в течение единичного интервала времени и на основании этого анализа принимает решение, какой из возможных сигналов присутствует на входе приемника. Сигнал на входе детектора имеет следующий вид: 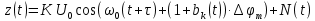 Алгоритм приема имеет следующий вид: 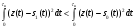 , где , где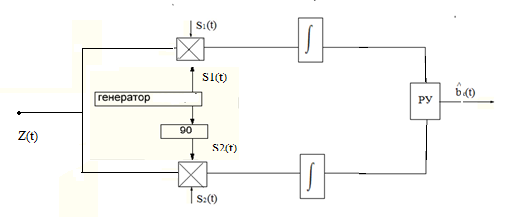 Рис. 7.2- Структурная схема ОФМ демодулятора Математическое описание: 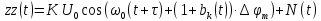 -аддитивная смесь OФМ сигнала и помехи -аддитивная смесь OФМ сигнала и помехи 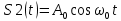 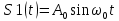 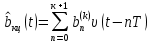 Декодер имеет вид: 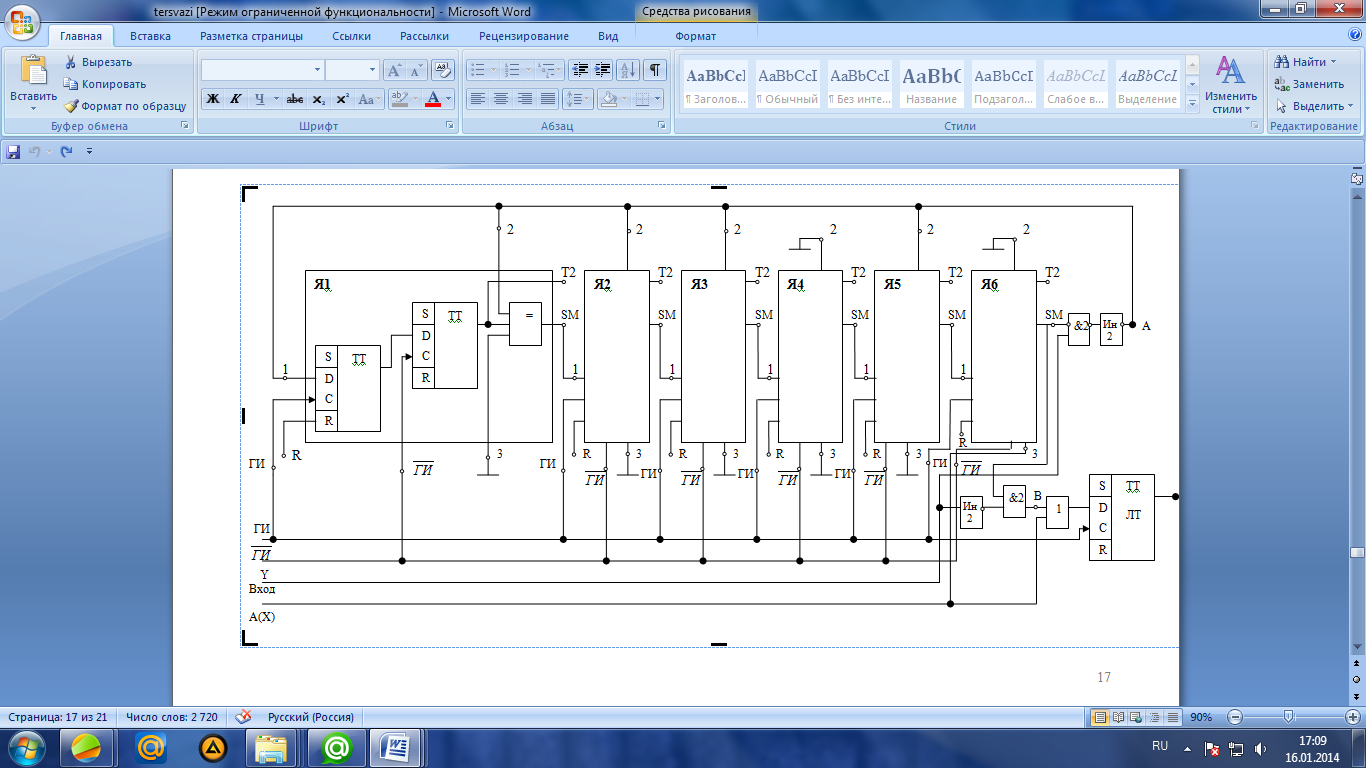 Рисунок 7.2 Принципиальная схема декодера БЧХ для систематического (13.25) кода Рассмотрим реализацию декодера на примере кода БЧХ (13.25), исправляющего две ошибки: порождающий полином В(х) = х8 + х7 + х6 + х4 + 1, длина кода n=15, количество проверочных символов p = deg B(x) = 8, количество информационных символов k = 7. Прямоугольниками на схеме обозначены элементы памяти, кружочками – устройства умножения на константу, записанную в кружочке, кружочками со знаком «+» обозначены сумматоры. Число элементов памяти равно степени многочленов b(X) и g(X). Цепи сдвига на схеме не показаны. Анализ: Данный кодер отличает то полезное свойство, что он не требует битовых операций и обеспечивает легкую смену кодового полинома. В силу этих обстоятельств легко выполняется как аппаратная, так и программная реализация такого кодека для БЧХ кода 8 Анализ качественных показателей разрабатываемой системы передачи информации. Вероятность ошибки не зависит от передаваемого символа. Она одинакова для всех двоичных систем при одинаковых энергиях сигнала. На рисунке 8.1 представлена зависимость Pош( 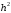 ). Все широкополосные системы модуляции обеспечивают высокую помехоустойчивость при условии, что отношение сигнала Рвх к помехе на входе больше некоторого предельного (порогового) значения Рпр. При Рвх<Рпр, широкополосные системы теряют свои преимущества, резко снижается помехоустойчивость и связь становится практически невозможной. ). Все широкополосные системы модуляции обеспечивают высокую помехоустойчивость при условии, что отношение сигнала Рвх к помехе на входе больше некоторого предельного (порогового) значения Рпр. При Рвх<Рпр, широкополосные системы теряют свои преимущества, резко снижается помехоустойчивость и связь становится практически невозможной.Определим зависимость вероятности ошибки от отношения сигнал-шум. Зависимость вероятности ошибки от отношения сигнал-шум при квазиоптимальном режиме и кодировании без проверки на четность имеет вид: 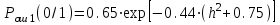 Зависимость вероятности ошибки от отношения сигнал-шум при квазиоптимальном режиме и кодировании с проверкой на четность имеет вид: 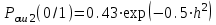 Зависимость вероятности ошибки от отношения сигнал-шум при оптимальном режиме имеет вид: 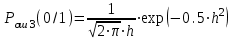 Зависимости 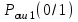 , , 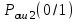 , ,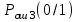 от от 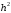 приведены в таблице 8.1. приведены в таблице 8.1.Таблица 8.1 – Зависимости 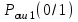 , , 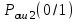 , ,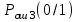 от от 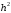
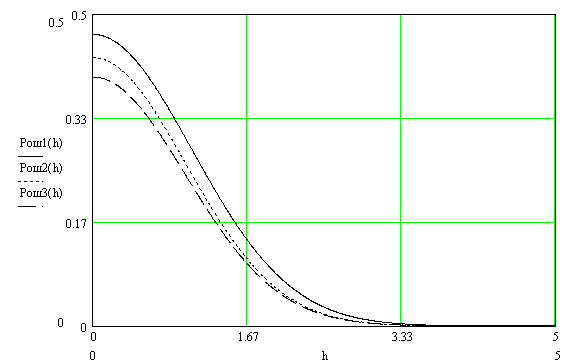 Рисунок 8.1 Зависимость вероятности ошибки от соотношения сигнал,шум для относительной фазовой модуляции Анализ: Когерентный прием - при модуляции используется информация о фазе принимаемого сигнала и требуется согласованность по фазе (когерентность) между принимаемым и опорным сигналами; решение о принимаемом сигнале выносится по мгновенным значениям напряжения сигнала. Вывод: Что сбой одной посылки приведет к сбою всех последующих, хотя, что при искажении фазы одной посылки исказиться может не более двух. Другое утверждени, что фаза сигнала "болтается" в среде распространения, особенно в ионосфере, как овечий хвост, и о передаче сигналов фазовым методом не может быть и речи. Медленном изменении фазы в интервале длительности двух посылок, на которых идет сравнение фаз, не убеждали. 9 Анализ показателей информационной эффективности системы и показателей эффективности по основным затратам Под эффективностью в широком смысле понимают степень использования каких-то материалов, средств, ресурсов, времени и т. д. В системах связи основными ресурсами можно считать пропускную способность канала С, ширину полосы частот Fk, мощность сигнала Ps. Для оценки степени их использования проф. А.Г. Зюко было предложено сравнивать их со скоростью передачи информации R. Введенные им коэффициенты эффективности являются важнейшими техническими показателями систем передачи информации. Наиболее общей оценкой эффективности системы связи является коэффициент использования пропускной способности канала. 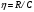 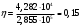 который называют информационной эффективностью. В реальных каналах скорость передачи информации всегда меньше пропускной способности, поэтому 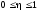 . .В системах с ограниченной полосой, например кабельных, важной характеристикой является коэффициент использования ширины полосы частот канала Fk 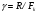 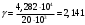 который называют частотной эффективностью. В ряде практических случаев удобной оценкой является коэффициент использования мощности сигнала Ps при спектральной плотности мощности помехи N0. 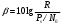 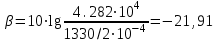 который называют энергетической эффективностью. Этот коэффициент играет важную роль в системах с ограниченной энергетикой, например в спутниковых. В результате проведенных расчетов была выполнена оценка эффективности системы связи и получены следующие результаты: значение коэффициента использования пропускной способности канала – 0,15; рассчитаны частотная и энергетическая эффективность 10 Расчет энергетического баланса системы Проанализируем прохождение передаваемого сообщения от источника к получателю. Для этого рассмотрим прохождение сигнала на различных этапах в разрабатываемой системе связи. Для выполнения энергетического баланса должно соблюдаться неравенство: 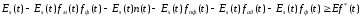 где f*(t) – чувствительность получателя информации по принимаемому сигналу. Произведем необходимый расчет. Определим мощность сигнала на входе. 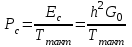 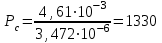 Рассчитаем баланс мощностей системы связи, учитывая что коэффициент усиления модулятора Км=2, коэффициент усиления демодулятора Кдм=2. Определим мощность сигнала на выходе модулятора. При этом необходимо учесть, что коэффициент передачи на резонансной частоте – коэффициент усиления. Мощность сигнала на выходе модулятора: 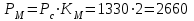 Примем минимальную чувствительность демодулятора, при которой обеспечивается заданная вероятность ошибки приема равной 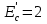 мкВ. Тогда получим минимальную мощность на входе демодулятора мкВ. Тогда получим минимальную мощность на входе демодулятора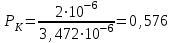 Определим ослабление в канале связи, учитывая минимальную чувствительность демодулятора и мощность сигнала на выходе модулятора. 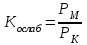 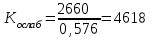 Определим мощность сигнала на выходе демодулятора. При этом необходимо учесть, что коэффициент передачи на резонансной частоте - коэффициент усиления. Мощность сигнала на выходе демодулятора: 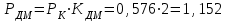 Вт ВтБаланс мощностей представлен на рисунке 10.1. 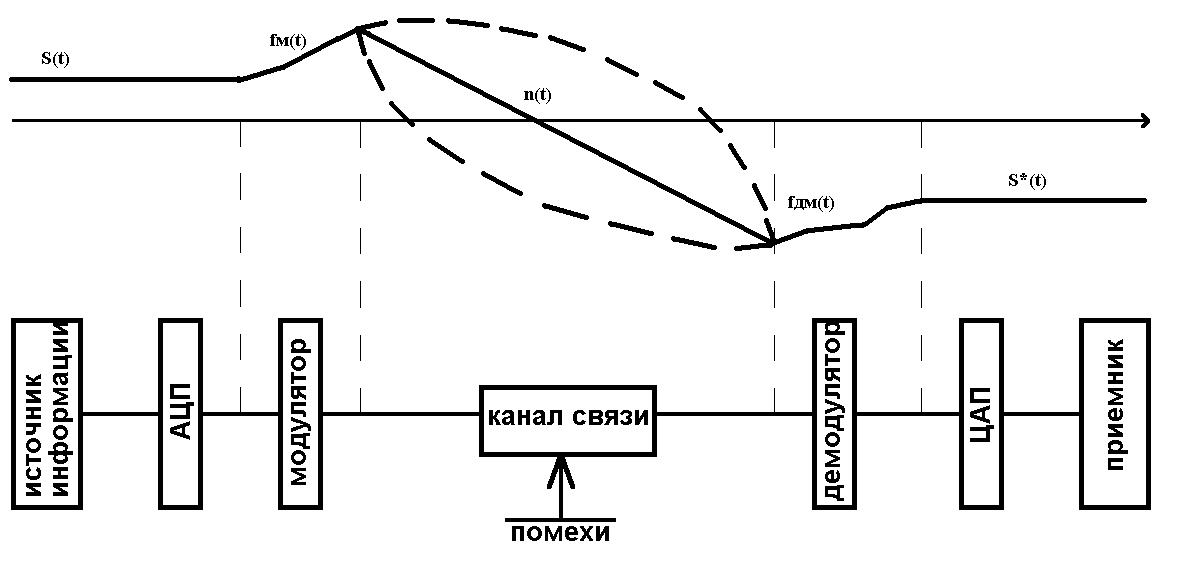 Рис.10.1. Структурная схема системы связи и ее энергетический баланс Рисунок 10.1 Баланс мощностей канала связи. где s(t) – первичный информационный сигнал, поступающий в систему связи от источника сообщений, в дальнейшем подвергающийся преобразованию в АЦП в цифровую форму, fМ(t) – передаточная функция модулятора, fДМ(t) – передаточная функция детектора, n(t) – воздействующие на передаваемый по линии связи сигнал шумы и помехи, s*(t) – сигнал, пришедший получателю, после преобразования в приемнике – конечный продукт системы передачи информации. |