Курсовая работа Цифровая обработка сигналов. Курсовая_цифровая обр сигналов_Абильмажинов_2 вар. Исходные данные к расчётам Вид модуляции офм
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
|
Исходные данные к расчётам: Вид модуляции – ОФМ Способ приёма сигнала – оптимальный, когерентный (сравнение полярностей) Ширина спектра сигнала - 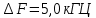 Число уровней квантования – N=256 Вероятность ошибки – Рош=3*10-6 Спектральная плотность мощности G0=10-5 Содержание
Введение Передача сообщения от источника к получателю с помощью радиотехнических методов осуществляется по радиоканалу. Основные элементы радиоканала передатчик, приемник и физическая среда, в которой происходит распространение электромагнитных волн. Средой распространения может быть как свободное пространство, так и специальные технические устройства волноводы, кабели и др. линии передачи. В то же время, передача сообщений по радиоканалу сопровождается разнообразными преобразованиями сигналов. Эти преобразования осуществляются посредством соответствующих физических систем радиотехнических цепей. Каждая радиотехническая цепь выполняет определенную операцию над сигналами, характер которой целиком зависит от внутренней структуры цепи. Так, принято различать усилители, фильтрующие частотно-избирательные системы, преобразователи формы электрических колебаний, модуляторы, детекторы и многие другие виды радиотехнических цепей, рассматриваемые в данном курсе. В любом реальном радиоканале помимо полезного сигнала неизбежно присут¬ствуют помехи, возникающие по многим причинам, из-за хаотического теплового движения электронов в элементах цепей, несовершенства контактов в аппаратуре, влияния соседних радиоканалов с близкими несущими частотами, наличия в пространстве шумового космического радиоизлучения и т. д. В наши дни радиосвязь является бурно развивающейся научно-прикладной областью. Говоря о ближайших перспективах ее развития, следует подчеркнуть тенденцию перехода все более высокочастотным диапазонам электромагнитных колебаний и волн. Так, колебания сверхвысокочастотного (СВЧ) диапазона, ранее применявшиеся в основном в радиолокации, стали широко использоваться в телевизионных, связных и телеметрических радиоканалах. Достигнуты большие успехи в создании лазерных линий связи с несущими частотами, лежащими в световом и инфракрасном диапазонах. Быстрыми темпами развивается элементная база радиотехники и радиоэлектроники. Если традиционные радиотехнические цепи представляли собой почти исключительно комбинации линейных и нелинейных электрических цепей, то сейчас интенсивно исследуются и внедряются в практику функциональные устройства и системы, производящие обработку сигналов за счет специфических волновых и колебательных явлений в твердых телах полупроводниках, диэлектриках и магнитных материалах. Огромную роль в современной радиосвязи играют изделия микроэлектронной технологии. Доступные, недорогие, надежные и быстродействующие интегральные микросхемы - решающим образом изменили облик многих областей радиосвязи. Микроэлектроника обусловила широкий переход к принципиально новым цифровым способам обработки и преобразования радиотехнических сигналов. Есть все основания ожидать, что отрасли радиотехники будут и впредь расширяться и развиваться на базе прогресса во многих смежных областях науки и техники. 1 Разработка в аналитическом, структурном, расчётно-графическом виде системы связи для амплитудной модуляции и неоптимального способа приёма В соответствии с заданием нам дана функциональная схема системы передачи сообщений изображенная на рисунке 1.1. Пусть требуется передать некоторое сообщение s(t), которое на выходе передающего устройства приняло вид канального сигнала u(t). При передаче сигнал искажается, и на него могут накладываться помехи: аддитивные η(t) и мультипликативные M(t). Приемное устройство обрабатывает принятое колебание z(t)=M(t)∙u(t)+η(t) и восстанавливает по нему сообщение 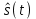 , которое с некоторой погрешностью отображает переданное сообщение. , которое с некоторой погрешностью отображает переданное сообщение. Рисунок 1.1 Функциональная схема системы связи Для того чтобы дать математическое описание канала необходимо и достаточно указать множество сигналов, которые могут быть поданы на его вход, и для любого допустимого входного сигнала задать случайный процесс на его выходе. Задать процесс – это значит задать в той или иной форме распределение вероятностей. Математическое описание передающей части устройства: 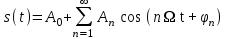 – сигнал на входе системы связи, – сигнал на входе системы связи,A0-постоянная составляющая An-амплитуда n-й гармоники n-номер гармоники Ω-частота первой гармоники φn-фаза n-й гармоники 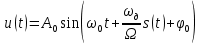 -частотно модулированныйсигнал -частотно модулированныйсигнална выходе модулятора ; A0-амплитуда несущего колебания 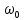 -центральная несущая частота -центральная несущая частота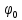 -начальная фаза -начальная фаза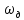 -девиация частоты -девиация частоты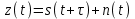 - аддитивная смесь сигнала и шума; - аддитивная смесь сигнала и шума;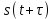 -сигнал задержанный на время τ -сигнал задержанный на время τn(t)-помеха(шум) в канале связи 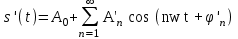 – сигнал на выходе; – сигнал на выходе;A0-постоянная составляющая An-амплитуда n-й гармоники принятого сигнала n-номер гармоники принятого сигнала Ω-частота первой гармоники принятого сигнала φn-фаза n-й гармоники принятого сигнала 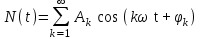 -помеха(белый шум) с гауссовским распределением . -помеха(белый шум) с гауссовским распределением . Плотность вероятности помехи 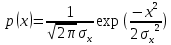 Математическое ожидание m=0 Спектральная плотность мощности G0= 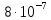 В2/Гц В2/Гц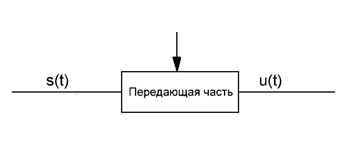 s0(t) Рисунок 1.2 Функциональная схема передатчика сообщений Математическое описание функциональной схемы системы: 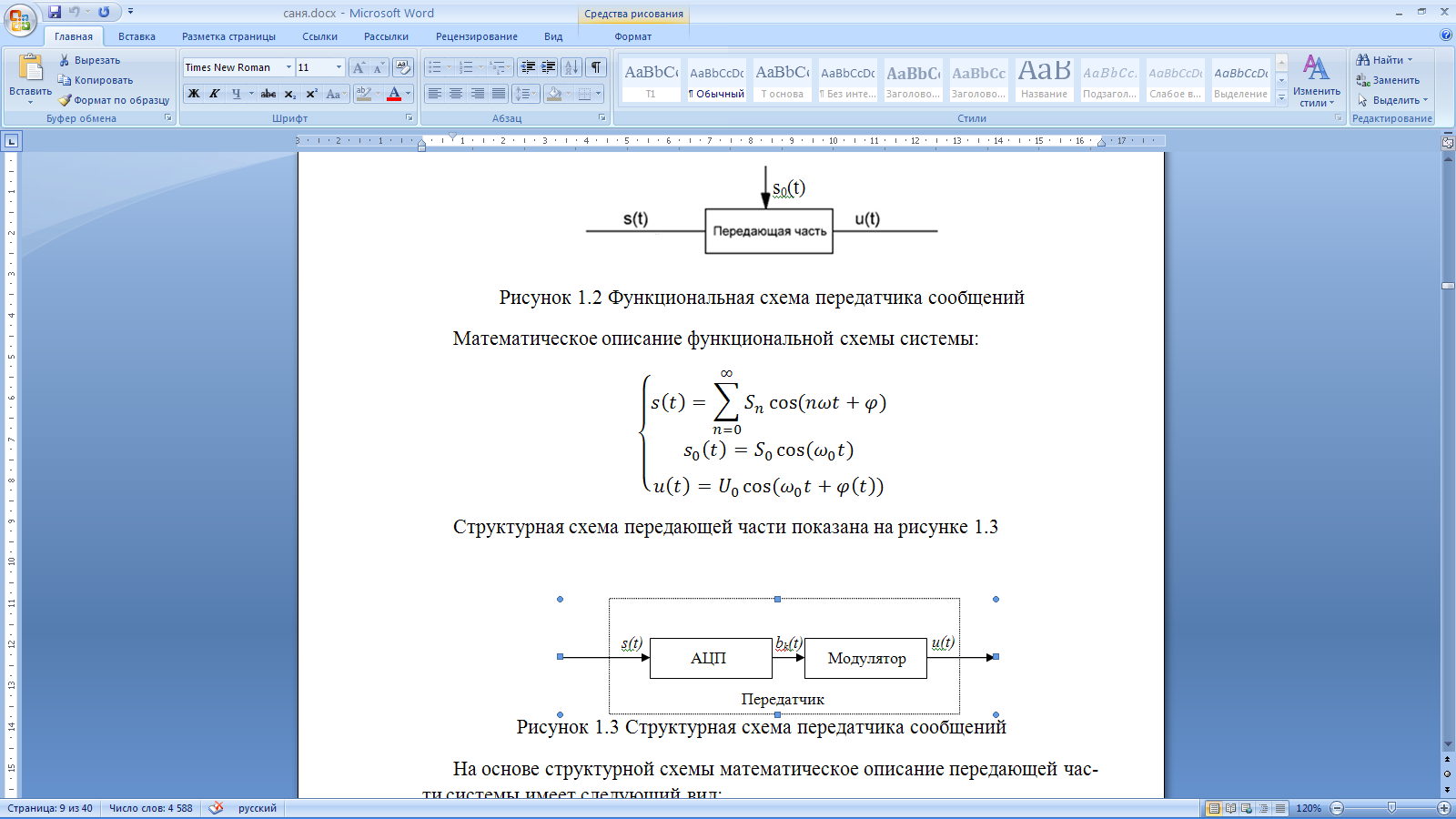 Структурная схема передающей части показана на рисунке 1.3 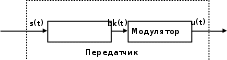 АЦП Рисунок 1.3 Структурная схема передатчика сообщений На основе структурной схемы математическое описание передающей части системы имеет следующий вид: 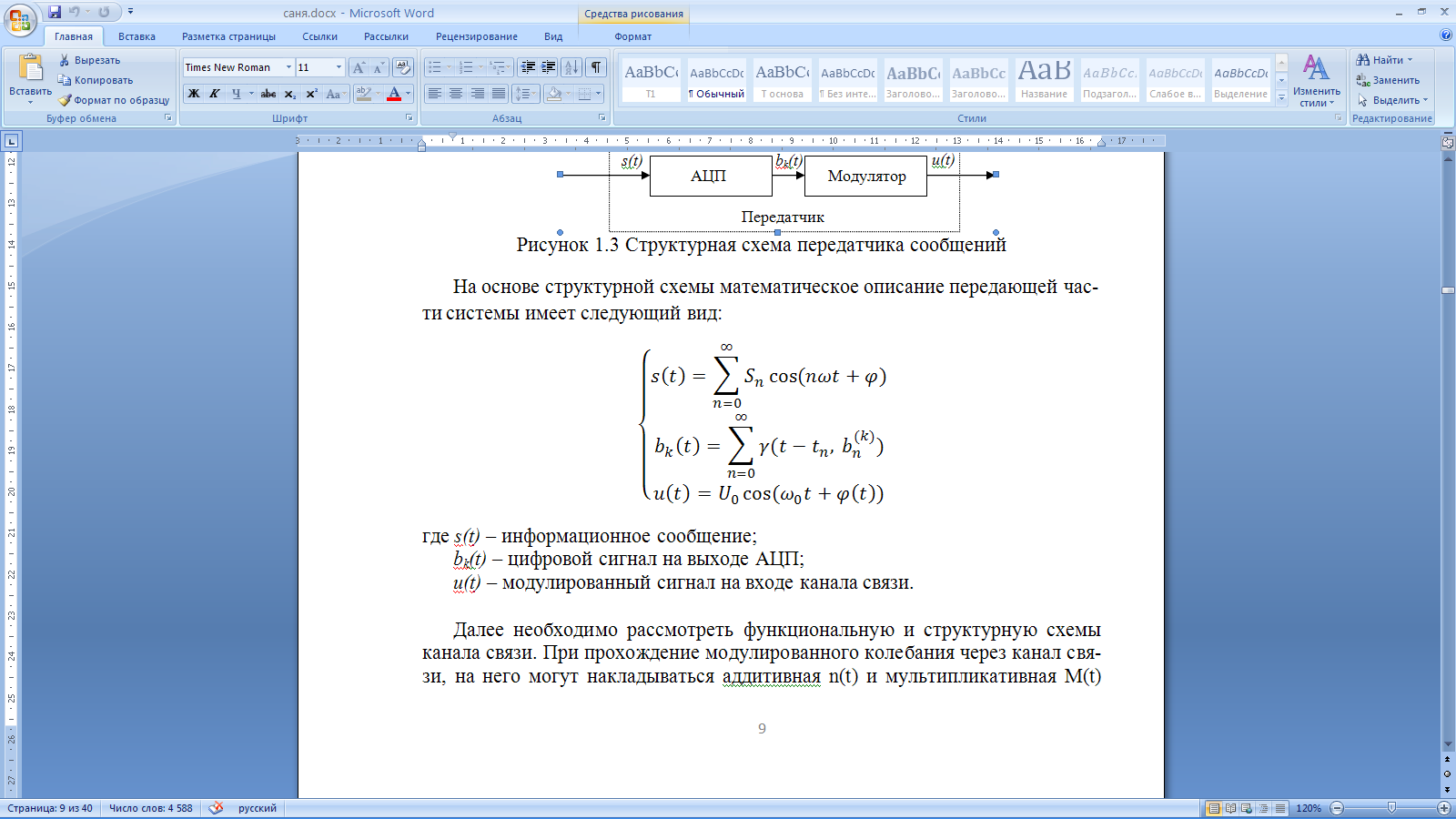 где s(t) – информационное сообщение; bk(t) – цифровой сигнал на выходе АЦП; u(t) – модулированный сигнал на входе канала связи. Далее необходимо рассмотреть функциональную и структурную схемы канала связи. При прохождение модулированного колебания через канал связи, на него могут накладываться аддитивная n(t) и мультипликативная M(t) помехи. Следовательно, функциональная и структурная схемы канала будут иметь вид, как показано на рисунке 1.4 и 1.5 соответственно.  Рисунок 1.4 Функциональная схема канала связи 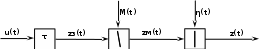 Рисунок 1.5 Структурная схема канала связи Исходя из структурной схемы, канал связи будет иметь следующее математическое описание: 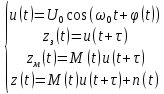 где u(t) – модулированный сигнал на входе канала связи; 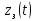 – сигнал с задержкой; – сигнал с задержкой;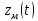 – сигнал с мультипликативной помехой; – сигнал с мультипликативной помехой;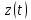 – сигнал на выходе канала связи, представляющий собой смесь аддитивной и мультипликативной помех. – сигнал на выходе канала связи, представляющий собой смесь аддитивной и мультипликативной помех.Следующим этапом идёт рассмотрение функциональной (рис. 1.6) и структурной (рис. 1.7) схем принимающей части системы передачи сообщений.  Рисунок 1.6 Функциональная схема приемной части  Демодулятор Рисунок 1.7 Структурная схема приемной части Математическое описание приёмной части системы: 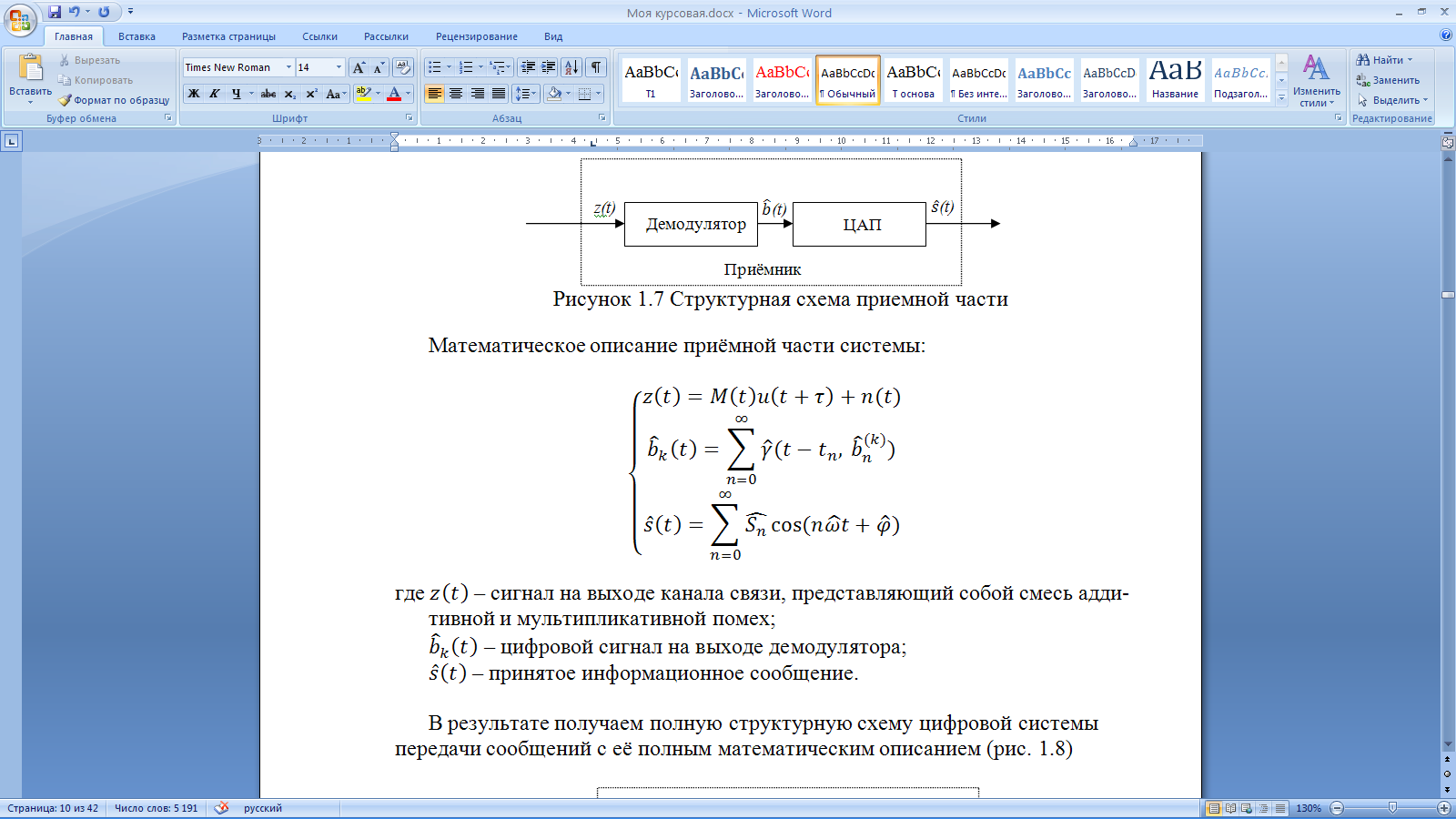 где 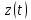 – сигнал на выходе канала связи, представляющий собой смесь аддитивной и мультипликативной помех; – сигнал на выходе канала связи, представляющий собой смесь аддитивной и мультипликативной помех;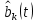 – цифровой сигнал на выходе демодулятора; – цифровой сигнал на выходе демодулятора;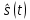 – принятое информационное сообщение. – принятое информационное сообщение.В результате получаем полную структурную схему цифровой системы передачи сообщений с её полным математическим описанием (рис. 1.8) 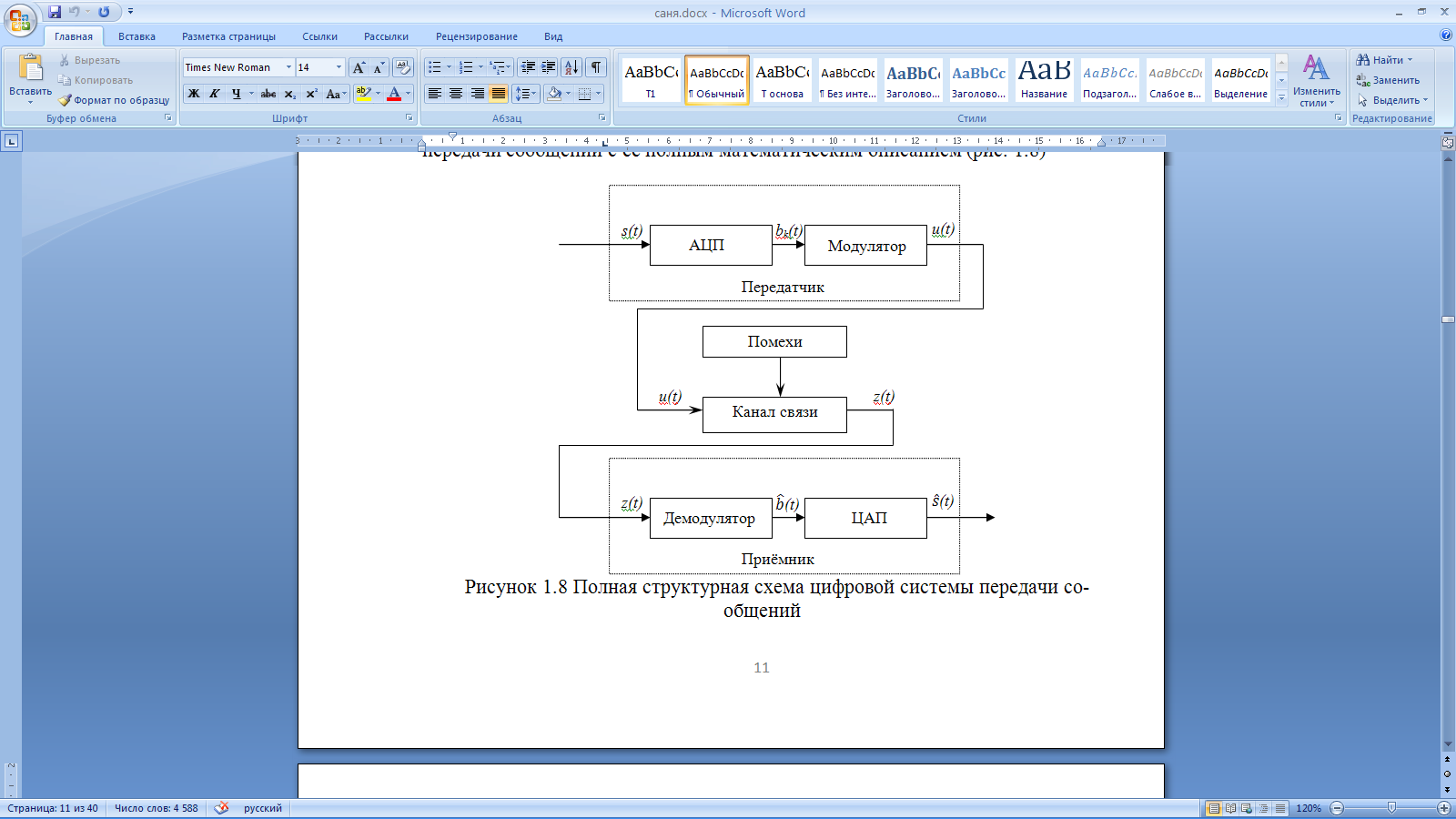 Рисунок 1.8 Полная структурная схема цифровой системы передачи сообщений Полное математическое описание будет иметь следующий вид: 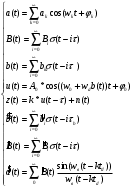 Анализ. Перед фазовым модулятором в цепь модулирующего дискретного сигнала подключается специальное перекодирующее устройство‚ обеспечивающее требуемое правило формирования ОФМ. Изменение фазы несущей частоты происходит только при подаче единичных элементов дискретной последовательности. Это перекодирующее устройство называется относительным кодером. Кодер содержит два блока: сумматор по модулю два и линию задержки на длительность элемента сигнала τи‚ представленную элементом памяти. На выходе фазового модулятора получаем ОФМ сигнал‚ который поступает в канал связи‚ а оттуда в приёмник на основе сравнения полярностей Вывод. Суть оптимального метода приема заключается в том, что на приемной стороне о передаваемом сигнале известны первичные данные: частота, фаза, длительность, момент прихода. Поэтому, в полученных сигналах возможные отклонения от передаваемых сигналов сводятся к минимуму. 2 Преобразование сигналов в АЦП Предполагая, что передаваемый информационный сигнал является аналоговым с шириной спектра ΔF=5,0 кГц‚ описываю преобразования, которым он повергается в АЦП при переходе к первичному цифровому сигналу ИКМ. Число уровней квантования N=256. В ИКМ аналоговый первичный сигнал подвергается преобразованию в цифровую форму с помощью трёх операций: дискретизации во времени (выборка значений аналогового сигнала с интервалом 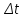 )‚ квантования по амплитуде (выборочное значение аналогового сигнала заменяется ближайшим значением уровня квантования) и кодирования (значение уровня квантования преобразуется в двоичное число). )‚ квантования по амплитуде (выборочное значение аналогового сигнала заменяется ближайшим значением уровня квантования) и кодирования (значение уровня квантования преобразуется в двоичное число).Таким образом‚ АЦП ИКМ должен содержать  дискретизатор‚ квантователь и кодирующее устройство (рис. 2.1). дискретизатор‚ квантователь и кодирующее устройство (рис. 2.1). Рисунок 2.1 Аналогово-цифровой преобразователь Математическое описание процессов, которым подвергается сигнал в АЦП может быть представлено в виде следующей системы уравнений: 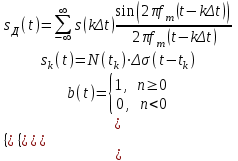 где sД(t) – дискретизированный сигнал; k – отсчет аналогового сигнала; fm – верхняя частота спектра сигнала; Δt – интервал дискретизации; sk(t) – квантованный сигнал; N(tk) – число квантов; tk– шаг квантования; σ(t– tk) – единичная функция; b(t) – цифровой сигнал; n – значение амплитуды квантованного сигнала данного кванта. По теореме Котельникова проведем дискретизацию для одиночного сигнала, определим интервал дискретизации. В соответствии с теоремой Котельникова сигнал s(t) ограниченный по спектру наивысшей частотой, можно представить рядом  где fm– верхняя частота спектра сигнала, в нашем случае 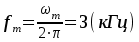 тогда, ωm = тогда, ωm =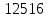 рад/с рад/с 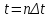 - интервал между двумя отсчетными точками на оси времени - интервал между двумя отсчетными точками на оси времени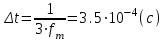 Количество выборок за τи: 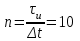 , , Далее используя выражение представленное выше проводится квантование сигнала с шагом квантования Δ = 2у.е. 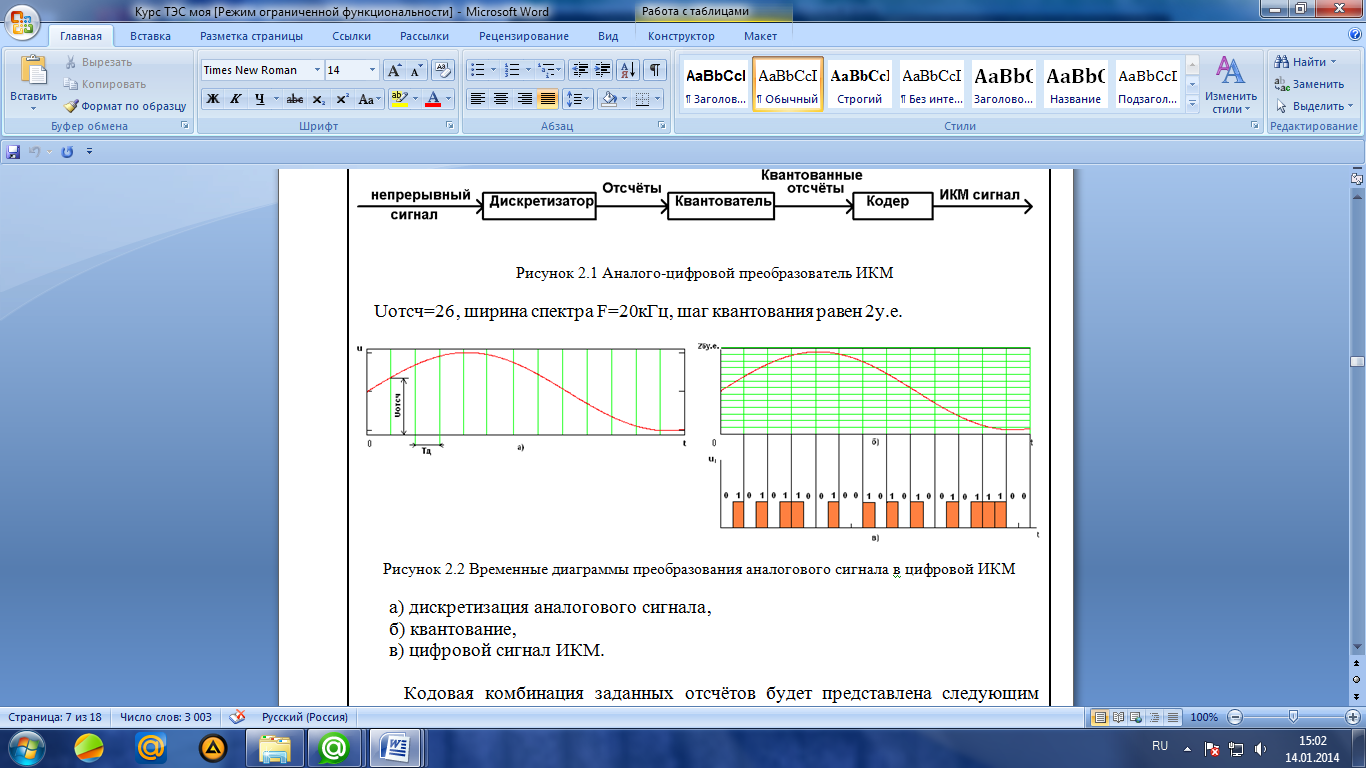 Рисунок 2.2 Исходный аналоговый, квантованный и дискретизированный сигнал во временной и частотной областях. а) дискретизация аналогового сигнала‚ б) квантование‚ в) цифровой сигнал ИКМ. Кодовая комбинация заданных отсчётов будет представлена следующим образом: u1=00011.01010.10010.00101.10100.01010.11000 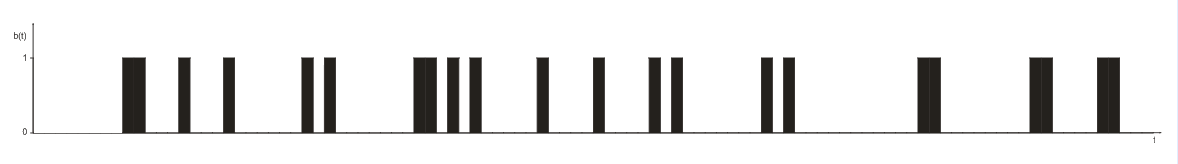 Рисунок 2.3 Цифровой сигнал на выходе АЦП Следующим этапом является кодирование сигнала. Требуемое число символов (импульсов и пауз) n в одной кодовой группе зависит от общего квантовых уровней (ступеней) N=256.Так как каждая ячейка в группе может быть использована для передачи либо импульса, либо паузы, то при числе ячеек n число различных комбинаций равно 2n. Таким образом, получается условие N=2n, откуда: n = log2N В нашем случае получаем: n = log2256=8. То есть кодовые группы содержат по девять ячеек. Заполнение каждой ячейки импульсом или паузой может быть определено путем перевода числа, выражающего величину выборки в десятичной системе счисления, в число, выраженное в двоичной системе счисления, с помощью нулей (паузы) и единиц (импульсы). При кодировании значений напряжения |
