курсовая. КР Подз гидр Метод (2). Исходные данные Определение коэффициента совершенства скважины
 Скачать 3.2 Mb. Скачать 3.2 Mb.
|
|
Содержание Исходные данные Определение коэффициента совершенства скважины Определение установившегося дебита одиночной скважины Определение коэффициентов продуктивности скважины при различных вариантах расположения скважины в пласте Оценка применимости линейного закона Дарси для рассматриваемых случаев фильтрации нефти Определение давления на различных расстояниях от скважины Определение условного времени отбора нефти из пласта при поддержании давлений Рк и Рс Определение изменения дебита скважины, расположенной в центре пласта Определение дебита каждой скважины и суммарного дебита, если данный круговой пласта разрабатывается пятью скважинами Определение дебита кольцевой батареи скважин Определение изменения распределения давления и дебита одиночной скважины, расположенной в центре кругового пласта, при стягивании контура нефтеносности под напором контурных вод Определение фронтовой водонасыщенности Список литературы Исходные данные скважина нефть фильтрация Вариант №….. Горизонтальный однородный круговой пласт имеет радиус контура питания Rк = 8 км, = 8000 м Мощность пласта h= 22 м Коэффициент пористости пласта m = 0,18 Коэффициент проницаемости пласта К= 1* 10-12 м2 Динамический коэффициент вязкости нефти μн = 12 мПа * с Плотность нефти ρн = 850 кг/м3 Коэффициент сжимаемости нефти βн = 1,04 * 10-9 Па-1 Коэффициент сжимаемости породы пласта βс = 0,72 * 10-10 Па-1 Водонасыщенность нефтяного пласта σ0 = 12% Коэффициент вязкости пластовой воды μв = 1,2 мПа * с Коэффициент сжимаемости пластовой воды βв = 4,6 * 10-10 Па-1 Пласт вскрывается скважинами на глубину b = 18 м Диаметр скважины Dс = 24,8 см Забой скважины обсажен и перфорирован на 1 м n=10 шт. Диаметр отверстий d0 = 16 мм. Глубина проникновения пуль в породу l` = 100 мм. Давление на контуре питания Рк = 16 МПа Забойное давление Рс = 13 МПа Рассчитать параметры фильтрации нефти к скважине и группе скважин при различных вариантах их расположения в плоском круговом пласте с ограниченным контуром питания для водонапорного и упругого режимов работы пласта. Определение коэффициента совершенства скважины Коэффициент совершенства скважины определяем по формуле: 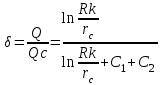 (1) (1)где: С1 – безразмерная величина, определяющая дополнительное фильтрационное сопротивление, обусловленное несовершенством скважины по степени вскрытия пласта; С2 – безразмерная величина, определяющая дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по характеру вскрытия пласта. Для определения коэффициента С1 используем график Щурова а = h / Dc = 22 / 0.248 = 88.7 Находим относительное вскрытие пласта: 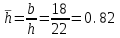 С1 = 0,75 С1 = 0,75С2 – определяем по графику Щурова l = l` / Dc = 100 / 248 = 0.4 α0 = d0 / Dc = 16 / 248 = 0.064 n* Dc = 10 * 24.8 = 10 * 0.248 = 2.48 C2 = 1.8 Находим радиус скважины rc = Dc / 2 = 24.8 / 2 = 0.248 / 2 = 0.124 м Находим коэффициент совершенства скважины 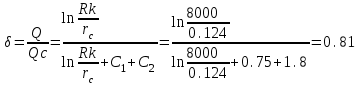 Определение установившегося дебита одиночной скважины для следующих вариантов ее расположения в круговом пласте Определяем установившейся дебит одиночной скважины Q для следующих вариантов ее расположения в круговом пласте: а) в центре б) на расстоянии 0,1 Rк от центра в) на расстоянии 0,5 Rк от центра г) на расстоянии 0,1 Rк от контура или 0,9 Rк от центра а) Объемный дебит гидродинамически совершенной скважины, расположенной в центре кругового пласта, определяется по формуле Дюпюи: 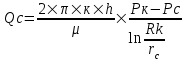 (2) (2)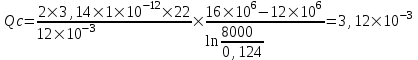 (м3/с) (м3/с)Объемный дебит гидродинамически несовершенной скважины, расположенной в центре кругового пласта: Q = Qс * δ = 3,12 х 10-3 х 0, 81 = 2,53 х 10-3 (м3/с) б) Определим установившейся дебит одиночной скважины на расстоянии 0,1 Rк от центра кругового пласта Дебит скважины, эксцентрично расположенной в круговом пласте, определяется по формуле: 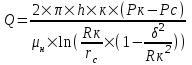 (3) (3)где: δ – расстояние от центра скважины до центра кругового пласта, δ = 0,1 * Rк = 0,1 * 8000 = 800 м 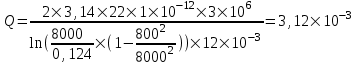 м3/с м3/св) Определим установившейся дебит одиночной скважины, расположенной на расстоянии 0,5 Rк от центра кругового пласта Дебит скважины, эксцентрично расположенной в круговом пласте, определяется по формуле: 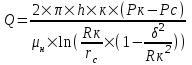 (4) (4)где: δ – расстояние от центра скважины до центра кругового пласта, δ = 0,5 * Rк = 0,5 * 8000 = 4000 м 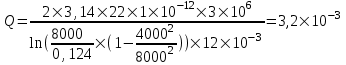 м3/с м3/сг) Определим установившейся дебит одиночной скважины, расположенной на расстоянии 0,1 Rк от контура кругового пласта Дебит скважины, эксцентрично расположенной в круговом пласте, определяется по формуле: 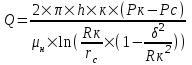 (5) (5)где: δ – расстояние от центра скважины до центра кругового пласта, δ = (1-0,1) * Rк = 0,9 * 8000 = 7200 м 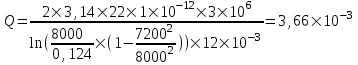 м3/с м3/сСтроим график зависимости дебита скважины от ее расположения в пласте. 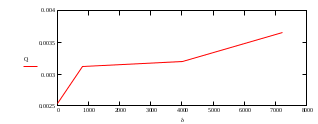 Определение коэффициентов продуктивности скважины при различных вариантах расположения скважины в пласте. Отношение дебита скважины Q к перепаду давления (депрессии) называется коэффициентом продуктивности скважины: 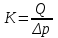 (6) (6)где: Δр = Рк – Рс = (16 – 13) х 106 = 3 х 106 Тогда 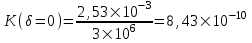 (м3 / Па*с) (м3 / Па*с)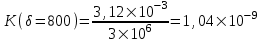 (м3 / Па*с) (м3 / Па*с)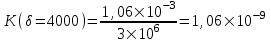 (м3 / Па*с) (м3 / Па*с)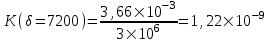 (м3 / Па*с) (м3 / Па*с)Зависимость дебита скважины Q от депрессии называется индикаторной линией. При плоскорадиальной фильтрации жидкости к скважине в условиях справедливости закона Дарси индикаторная линия представляет собой прямую, определяемую уравнением: 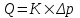 (7) (7)скважина расположена в центре кругового пласта ΔР1 = 1 МПа Q1 = 8,43 * 10-10 * 1 * 106 = 8,43 * 10-4 (м3/с) ΔР1 = 3 МПа Q1 = 8,43 * 10-10 * 3 * 106 = 2,53 * 10-3 (м3/с) ΔР1 = 5 МПа Q1 = 8,43 * 10-10 * 5 * 106 = 4,22 * 10-3 (м3/с) скважина расположена на расстоянии 0,1 Rк от центра кругового пласта ΔР1 = 1 МПа Q1 = 1,04* 10-9 * 1 * 106 = 1,04 * 10-3 (м3/с) ΔР1 = 3 МПа Q1 = 1,04 * 10-9 * 3 * 106 = 3,12 * 10-3 (м3/с) ΔР1 = 5 МПа Q1 = 1,04 * 10-9 * 5 * 106 = 5,2 * 10-3 (м3/с) скважина расположена на расстоянии 0,5 Rк от центра кругового пласта ΔР1 = 1 МПа Q1 = 1,06* 10-9 * 1 * 106 = 1,06 * 10-3 (м3/с) ΔР1 = 3 МПа Q1 = 1,06 * 10-9 * 3 * 106 = 3,18 * 10-3 (м3/с) ΔР1 = 5 МПа Q1 = 1,06 * 10-9 * 5 * 106 = 5,3 * 10-3 (м3/с) скважина расположена на расстоянии 0,1 Rк от контура питания кругового пласта ΔР1 = 1 МПа Q1 = 1,22 * 10-9 * 1 * 106 = 1,22 * 10-3 (м3/с) ΔР1 = 3 МПа Q1 = 1,22 * 10-9 * 3 * 106 = 3,66 * 10-3 (м3/с) ΔР1 = 5 МПа Q1 = 1,22 * 10-9 * 5 * 106 = 6,1 * 10-3 (м3/с) На основании результатов расчетов, строим индикаторные линии скважины при различных вариантах ее расположения в пласте. 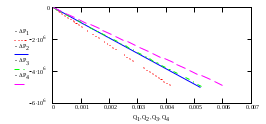 Оценка применимости линейного закона Дарси для рассматриваемых случаев фильтрации нефти. Применимость закона Дарси определяем по формуле Щелкочева: 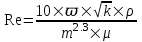 (8) (8)где: ω – скорость фильтрации на забое скважины m – пористость ω = Q0 / S где: S – площадь забоя , S = 2 * 3.14 * rc * b S = 2 * 3.14 * 0.124 * 18 = 14.016 м2 Определяем скорость фильтрации на забое скважины ω = 2,53 * 10-3 / 14,016 = 1,8 * 10-4 м3/с Данные подставляем в формулу Щелкочева: 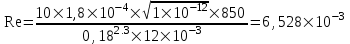 Число Ренольдса меньше соотношения 0,022 ≤ Reкр ≤ 0,29, значит происходит ламинарный режим фильтрации. Для данного режима фильтрации закон Дарси полностью применим. Определение давления на различных расстояниях от скважины Закон распределения давления в пласте определяется по формуле: 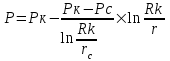 (9) (9)где: r - расстояние от оси скважины С учетом сжимаемости жидкости закон распределения давления в пласте определяется по формуле: 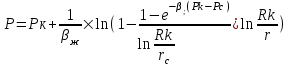 (10) (10)где: βж – коэффициент объемной сжимаемости жидкости, который определяется: βж = (1-σ0) * βн + σ0 х βв (11) Рассмотрим закон распределения давления при заданном забойном давлении Рс = 13 МПа для различных вариантов расположения скважины в пласте: скважина расположена в центре кругового пласта. при r = 0.5 м По формуле (9) закон распределения Р: 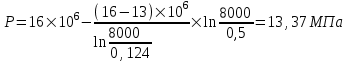 при r=1 м 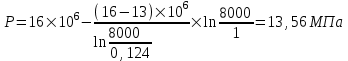 при r=2 м 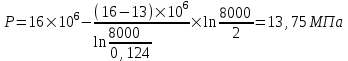 при r=5 м 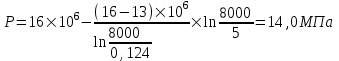 при r=10 м 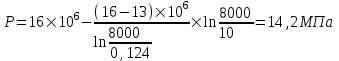 при r=100 м 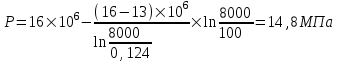 при r=1000 м 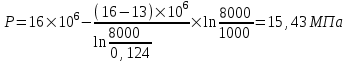 при r=2000 м 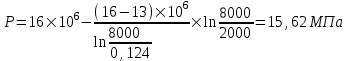 при r=4000 м 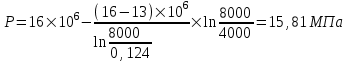 скважина расположена на расстоянии 0,1 Rк от центра кругового пласта По формуле (9) закон распределения Р: при r = 0.5 м 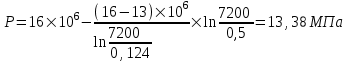 при r=1 м 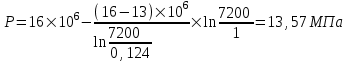 при r=2 м 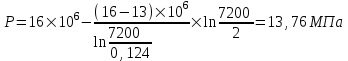 при r=5 м 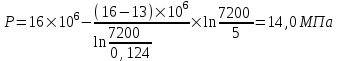 при r=10 м 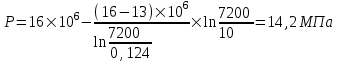 при r=100 м 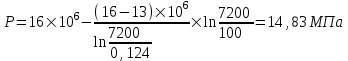 при r=1000 м 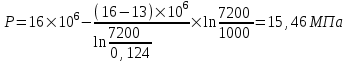 при r=2000 м 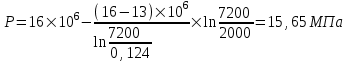 при r=4000 м 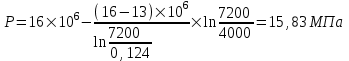 скважина расположена на расстоянии 0,5 Rк = 4000 м от центра кругового пласта. По формуле (9) закон распределения Р: при r = 0.5 м 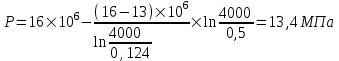 при r=1 м 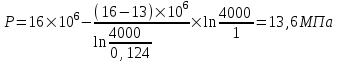 при r=2 м 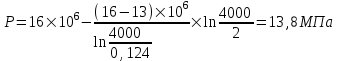 при r=5 м 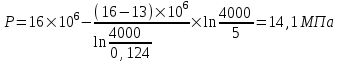 при r=10 м 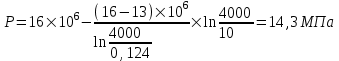 при r=100 м 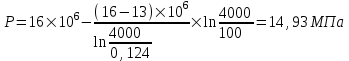 при r=1000 м 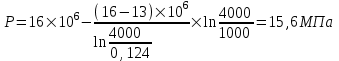 при r=2000 м 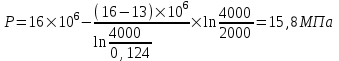 при r=4000 м 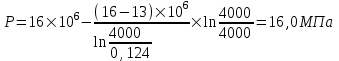 скважина расположена на расстоянии 0,1 Rк = 7200 м от контура кругового пласта По формуле (9) закон распределения Р: при r = 0.5 м 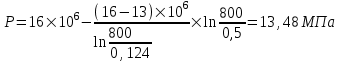 при r=1 м 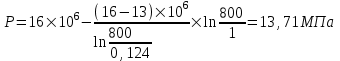 при r=2 м 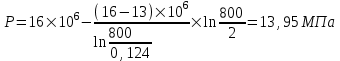 при r=5 м 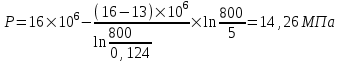 при r=10 м 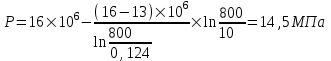 при r=100 м 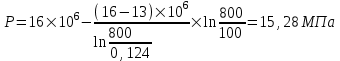 при r=1000 м 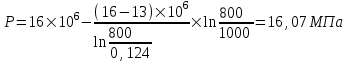 при r=2000 м 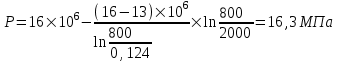 при r=4000 м 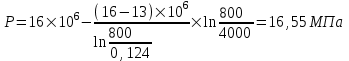 По полученным результатам строим кривые депрессии Р = Р(r). Средневзвешенное по объему порового пространства пластовое давление определяется по формуле: 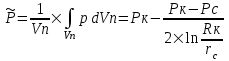 (11) (11)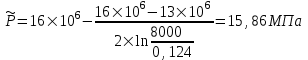 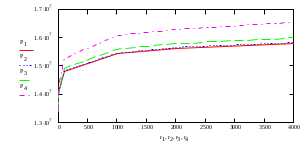 Определение условного времени отбора нефти из пласта при поддержании постоянных давлений Рк и Рс при расположении скважины в центре пласта Время отбора жидкости из кругового пласта определяется по формуле: 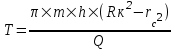 (12) (12)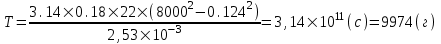 Определение изменения дебита скважины, расположенной в центре пласта, если на расстоянии 200 м расположить такую же скважину с тем же забойным давлением Используя принцип суперпозиции, рассчитаем забойные потенциалы и дебиты для скважин. Потенциал скорости фильтрации определяется по формуле: 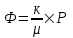 (13) (13)Значение потенциала в точке на расстоянии r: 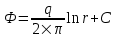 (14) (14)где: С – постоянная интегрирования. При совместной работе нескольких скважин результирующий потенциал в любой точке пласта равен алгебраической сумме потенциалов, обусловленных работой каждой отдельной скважины. Таким образом: 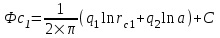 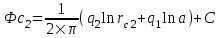 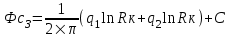 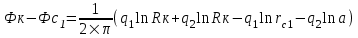 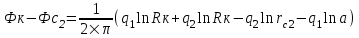 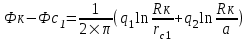 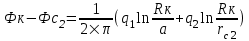 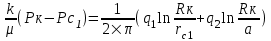 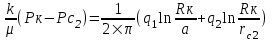 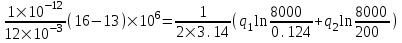 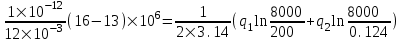 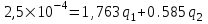 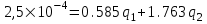 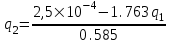 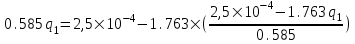 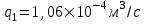 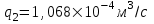 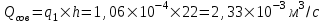 Дебит несовершенной скважины 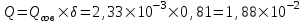 м3/с м3/сСледовательно, дебит скважины уменьшается. Определение дебита каждой скважины и суммарного дебита, если данный круговой пласт разрабатывается пятью скважинами Определяем дебит каждой скважины и суммарный дебит, если данный круговой пласт разрабатывается пятью скважинами, из которых 4 расположены в вершинах квадрата со стороной А = 500 м , а пятая - в центре. Все скважины идентичны и работают с одинаковым забойным давлением Рс. Поместим точку М на забой 1 скважины 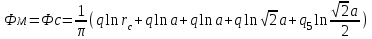 Поместим точку М на забой 5-ой скважины 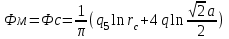 Поместим точку М на контур питания 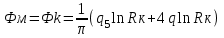 Получаем систему уравнения 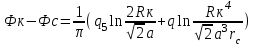 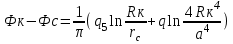 Так как 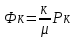 и и 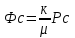 , то , то 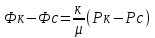 Тогда получаем следующую систему уравнения 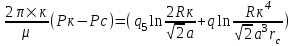 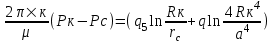 Получим 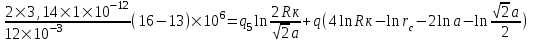 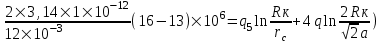 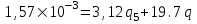 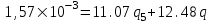 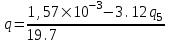 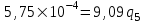 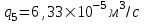 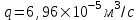 С учетом коэффициента совершенства Q = q * δ . Тогда дебиты скважин равны Q = 6,96 * 10-5 * 0. 81 = 5,64 *10-5 и Q5 = 6,96 * 10-5 * 0.81 = 5,63*10-5 м3/с. Суммарный дебит равен Qсум = 4Q + Q5 = 4 * 5,64*10-5 + 5,63*10-5 = 2,819 * 10-4 м3/с Определение дебита кольцевой батареи скважин, расположенных по кругу на расстоянии 0,6 Rк от центра Все скважины идентичны и работают с одинаковым забойным давлением Рс = 12 МПа, 0,6 Rк = 4800 м. Дебит одной скважины кольцевой батареи, состоящей из n скважин, в круговом пласте радиуса Rк, равен: 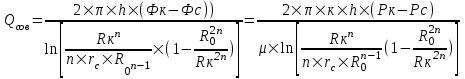 (15) (15)где: R0 – радиус батареи rc - радиус скважины Суммарный дебит кольцевой батареи несовершенных скважин определяется по формуле: 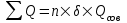 (16) (16)Определим дебит кольцевой батареи скважин при различном числе скважин n с учетом формул (15) и (16): а) n= 4 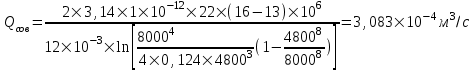 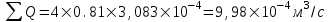 б) n = 5 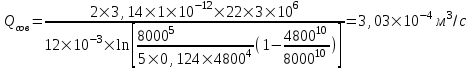 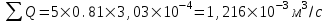 в) n = 6 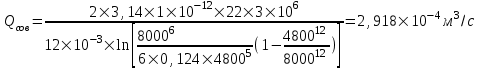 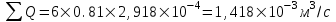 г) n = 8 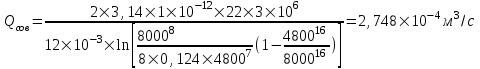 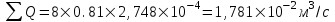 д) n = 10 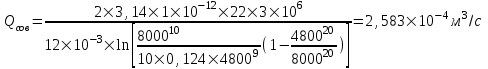 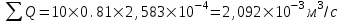 е) n = 12 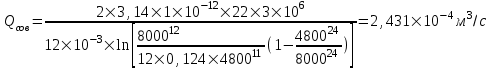 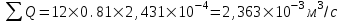 ж) n = 16 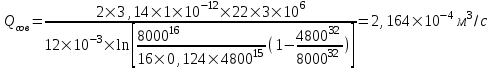 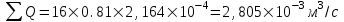 з) n=20 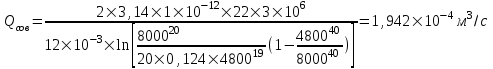 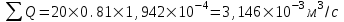 Определение изменения распределения давления и дебита одиночной скважины, расположенной в центре кругового пласта, при стягивании контура нефтеносности под напором контурных вод При плоскорадиальном вытеснении нефти водой дебит скважины определяется по формуле: 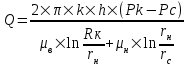 (17) (17)где: rн – координата (радиус) границы раздела нефть-вода в момент времени t. Таким образом при постоянной депрессии дебит скважины с темпом времени увеличивается. Закон распределения давления вдоль радиуса Р(r) выражается следующими соотношениями: - в водоносной области: 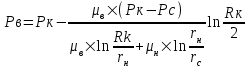 (18) (18)- в нефтяной области 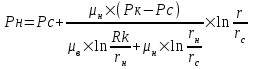 (19) (19)Время радиального перемещения контура нефтеносности от начального положения Ω0 (при t=0) до r определяется по формуле:  Определение дебита для случая расположения контура нефтеносности на расстоянии rн = Rк от оси скважины.  (м3/с) (м3/с)Q = Qс * δ = 3,12х 10-3 х 0, 81 = 2,53 х 10-3 (м3/с)   а) контур нефтеносности расположен на расстоянии rн = 0,75 Rк = 6000 м от оси скважины. 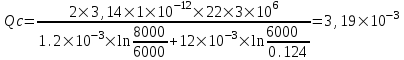 (м3/с) (м3/с)Q = Qс * δ = 3,19 х 10-3 х 0, 81 = 2,59 х 10-3 (м3/с) б) контур нефтеносности расположен на расстоянии rн = 0,5 Rк = 4000 м от оси скважины. 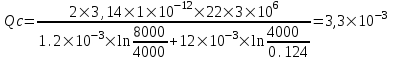 (м3/с) (м3/с)Q = Qс * δ = 3,3 х 10-3 х 0, 81 = 2,68 х 10-3 (м3/с) в) контур нефтеносности расположен на расстоянии rн = 0,25 Rк = 2000 м от оси скважины. 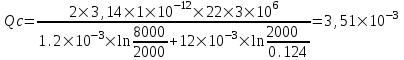 (м3/с) (м3/с)Q = Qс * δ = 3,51 х 10-3 х 0, 81 = 2,84 х 10-3 (м3/с) г) контур нефтеносности расположен на расстоянии rн = 0,01 Rк = 80 м от оси скважины. 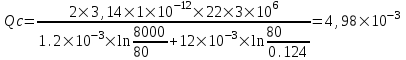 (м3/с) (м3/с)Q = Qс * δ = 4,98 х 10-3 х 0, 81 = 4,03 х 10-3 (м3/с) Определим изменение распределения давления для различных случаев расположения контура нефтеносности. а) контур нефтеносности расположен на расстоянии rн = 0,75 Rк = 6000 м от оси скважины. r = 0.01 Rк =80 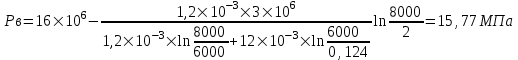 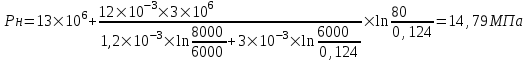 б) контур нефтеносности расположен на расстоянии rн = 0,5 Rк = 4000 м от оси скважины. r = 0.01 Rк =80 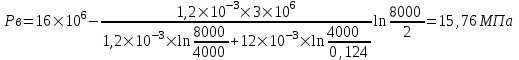 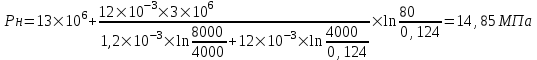 в) контур нефтеносности расположен на расстоянии rн = 0,25 Rк = 2000 м от оси скважины. в) контур нефтеносности расположен на расстоянии rн = 0,25 Rк = 2000 м от оси скважины.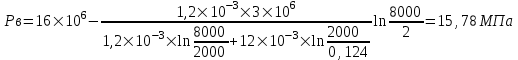 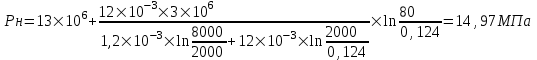 По полученным данным для указанных значений rн строим кривые депрессии давления в призабойной зоне (r ≤0,001 Rк) 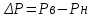 ΔР1 = 1,02 МПа ΔР2 = 0,98 МПа ΔР3 = 0,91 МПа ΔР4 = 0,81 МПа График зависимости дебита скважины от положения контура нефтеносности rн и кривые депрессии давления в призабойной зоне (r ≤0,001 Rк) 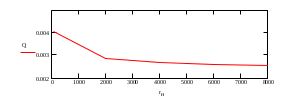 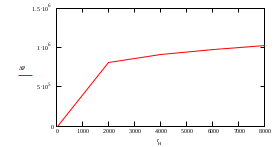 Время вытеснения всей нефти из кругового пласта рассчитаем по формуле (20) 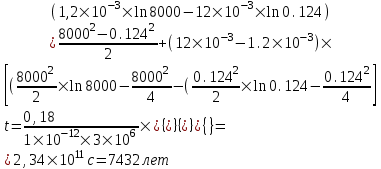 Определение фронтовой водонасыщенности Фронтовую водонасыщенность определяем графически, используя графики функции Леверетта . Проведя из начала координат к кривой f(σ) и опустив перпендикуляр из точки касания на ось σ, получим значение фронтовой водонасыщенности. σф = 50 %, а σср = 60 %, 2. Упругий неустановившийся режим Замкнутый горизонтальный круговой пласт с радиусом контура имеет начальное пластовое давление Рк. Одиночная скважина, расположенная в центре пласта, эксплуатируется при постоянном забойном давлении Рс. Определение упругого запаса нефти в пласте при уменьшении давления от Рк до Рс. Определение полного запаса нефти. Величина упругого запаса жидкости в пласте при снижении давления в нем на ΔР определяется по формуле: 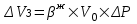 (21) (21)где: V0 – объем пласта; βж – коэффициент упругоемкости пласта 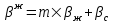 (22) (22)Объем пласта определяется по формуле: 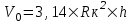 (23) (23)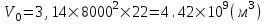 Коэффициент упругоемкости пласта 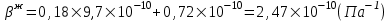 Упругий запас 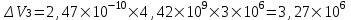 (м3) (м3)Полный запас нефти 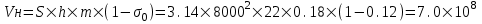 (м3) (м3)Определение изменения дебита скважины после пуска ее в эксплуатацию При пуске скважины в эксплуатацию в пласте возникают неустановившиеся процессы, которые проявляются, в частности, в изменении с течением времени дебитов, в перераспределении пластового давления. Темп перераспределения пластового давления в условиях упругого режима характеризуется коэффициентом пьезопроводности. 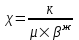 (24) (24)Для расчета изменения дебита скважины используем метод последовательной системы стационарных состояний. Приведенный радиус влияния при плоскорадиальном притоке упругой жидкости к скважине для случая постоянной депрессии 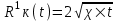 (25) (25)Коэффициент пьезопроводности: 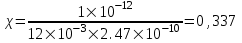 (м2/с) (м2/с)Определим значение приведенного радиуса влияния в различные моменты времени: 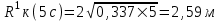 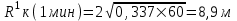 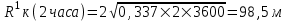 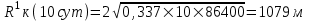 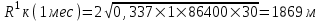 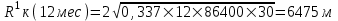 Объемный дебит скважины после пуска ее в эксплуатацию определяем 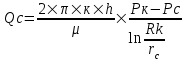 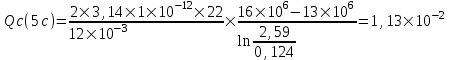 (м3/с) (м3/с)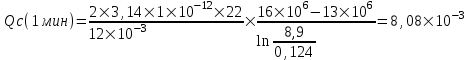 (м3/с) (м3/с)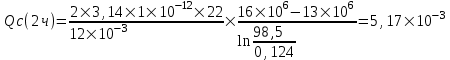 (м3/с) (м3/с)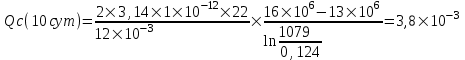 (м3/с) (м3/с)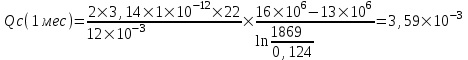 (м3/с) (м3/с)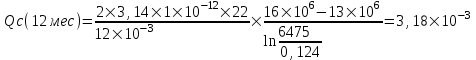 (м3/с) (м3/с)Список литературы Басниев К.С. , Кочина И.Н. «Подземная гидромеханика», М.: Недра, 1993 Евдокимова В.А. «Сборник задач по подземной гидравлике», М.Недра, 1979 Пыхачев Г.Б., Исаев Р.Г. «Подземная гидравлика», М.Недра, 1973 МУК «Подземная гидромеханика» к практическим и курсовой работе по курсу «Подземная гидромеханика», ГГТУ им П. О. Сухого, Гомель, 1996 Басниев К.С. «Подземная гидравлика», М.: Недра, 1986 |
