Практика. Теоретические сведения. Обработка ид нефтедобывающей скважины
 Скачать 2.02 Mb. Скачать 2.02 Mb.
|
Практическое занятие №1. Обработка индикаторных диаграмм нефте- и газодобывающих скважин в однородных пластах.Теоретические сведения.Обработка ИД нефтедобывающей скважиныПри подчинении фильтрации жидкости в пласте линейному закону, т.е. индикаторная линия имеет вид прямой, зависимость дебита гидродинамически совершенной скважины от депрессии на забое описывается формулой Дюпюи: 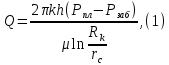 где 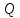 - дебит скважины, м3/с; - дебит скважины, м3/с;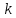 - проницаемость продуктивного пласта, мкм2; - проницаемость продуктивного пласта, мкм2;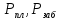 - пластовое и забойное давление, Па; - пластовое и забойное давление, Па; h - толщина пласта, м; 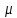 - вязкость жидкости, Па∙с; - вязкость жидкости, Па∙с;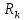 и и 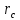 - радиус контура питания и радиус скважины, м. - радиус контура питания и радиус скважины, м. Считается, что давление на забое через некоторое время после остановки скважины становится примерно равным среднему пластовому давлению, установившемуся на круговом контуре с радиусом, равным половине среднего расстояния между исследуемой скважиной и соседними, ее окружающими. Индикаторная диаграмма 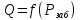 предназначена для оценки величины пластового давления, которое можно определить путем продолжения индикаторной линии до пересечения с осью ординат (Рисунок 1). Это соответствует нулевому дебиту, т. е. скважина не работает и предназначена для оценки величины пластового давления, которое можно определить путем продолжения индикаторной линии до пересечения с осью ординат (Рисунок 1). Это соответствует нулевому дебиту, т. е. скважина не работает и 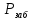 стремится к стремится к 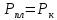 . .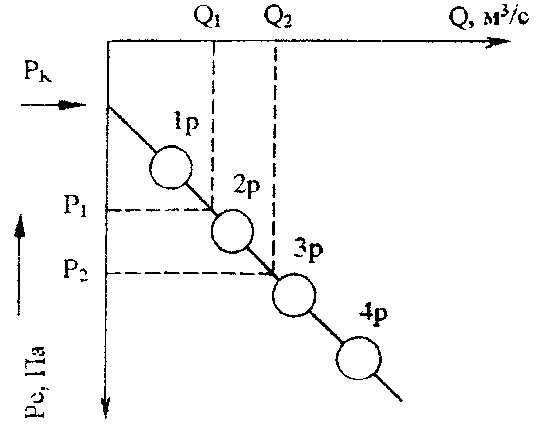 Рисунок 1 – Индикаторная диаграмма 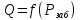 Индикаторная диаграмма 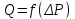 (Рисунок 2) строится для определения коэффициента продуктивности скважин К. (Рисунок 2) строится для определения коэффициента продуктивности скважин К.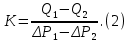 В пределах справедливости линейного закона фильтрации жидкости, т.е. при линейной зависимости 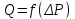 , коэффициент продуктивности является величиной постоянной и численно равен тангенсу угла наклона индикаторной линии к оси дебитов (оси абсцисс). По коэффициенту продуктивности скважин, определенному методом установившихся отборов, можно вычислить также другие параметры пласта. , коэффициент продуктивности является величиной постоянной и численно равен тангенсу угла наклона индикаторной линии к оси дебитов (оси абсцисс). По коэффициенту продуктивности скважин, определенному методом установившихся отборов, можно вычислить также другие параметры пласта.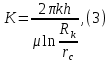 откуда коэффициент гидропроводности 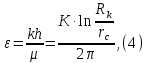 и проницаемость пласта в призабойной зоне 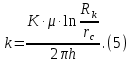 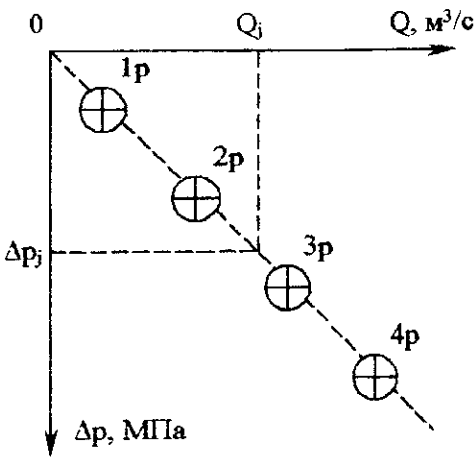 Рисунок 2 – Индикаторная диаграмма 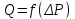 Приведенные выше формулы справедливы для случая исследования гидродинамически совершенной скважины (вскрывшей пласт на всю его толщину и имеющей открытый забой, Рисунок 3, а) и измеряемые величины (дебит, динамическая вязкость и др.) приведены к пластовым условиям. 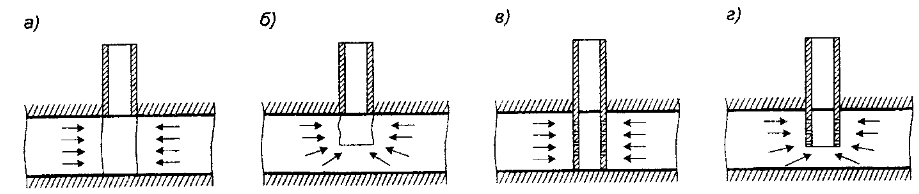 Рисунок 3 – Виды несовершенства скважин: а - скважина совершенная; б - несовершенная по степени вскрытия; в - несовершенная по характеру вскрытия; г - несовершенная по степени и характеру вскрытия Если скважина с открытым забоем вскрывает пласт не на всю толщину, а только на некоторую величину b, или если скважина сообщается с пластом через отдельные отверстия, то фильтрация жидкости или газа будет пространственной (трехмерной), а скважина - гидродинамически несовершенной. Различают три вида несовершенства скважин: 1) скважина гидродинамически несовершенна по степени вскрытия пласта - это скважина с открытым забоем, вскрывшая пласт не на всю толщину (Рисунок 3, б); 2) скважина гидродинамически несовершенна по характеру вскрытия пласта - скважина, вскрывшая пласт от кровли до подошвы, но сообщающаяся с пластом через отверстия в колонне труб, в цементном кольце или в специальном фильтре (Рисунок 3, в); 3) скважина гидродинамически несовершенна как по степени, так и по характеру вскрытия пласта (Рисунок 3, г). В случае измерения массовых дебитов гидродинамически несовершенной скважины в поверхностных условиях необходимо это учесть следующим образом. По коэффициенту продуктивности К определяются гидропроводность и проницаемость пласта в зоне, примыкающей к скважине: 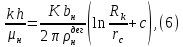 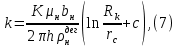 где 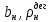 - объемный коэффициент и плотность дегазированной нефти; - объемный коэффициент и плотность дегазированной нефти;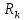 - радиус контура питания; - радиус контура питания;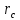 - радиус скважины по долоту; - радиус скважины по долоту; h - эффективная толщина вскрытого скважиной пласта; с - дополнительное фильтрационное сопротивление притоку жидкости к скважине, вызванное ее несовершенством (по степени или по характеру вскрытия). Графический метод В.И. Щурова определения смешанного несовершенства Для смешанного несовершенства величина с выражается суммой 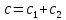 , каждая из составляющих которой может быть определена по кривым В.И. Щурова (см. Приложение 1), исходя из степени вскрытия пласта , каждая из составляющих которой может быть определена по кривым В.И. Щурова (см. Приложение 1), исходя из степени вскрытия пласта 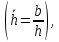 плотности перфорации и диаметра скважины (nD), диаметра отверстий в колонне плотности перфорации и диаметра скважины (nD), диаметра отверстий в колонне 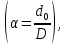 и глубины каналов в пласте при перфорации и глубины каналов в пласте при перфорации 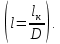 Величина 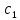 , представлена на рисунке 4 в зависимости от параметров , представлена на рисунке 4 в зависимости от параметров 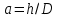 и и 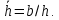 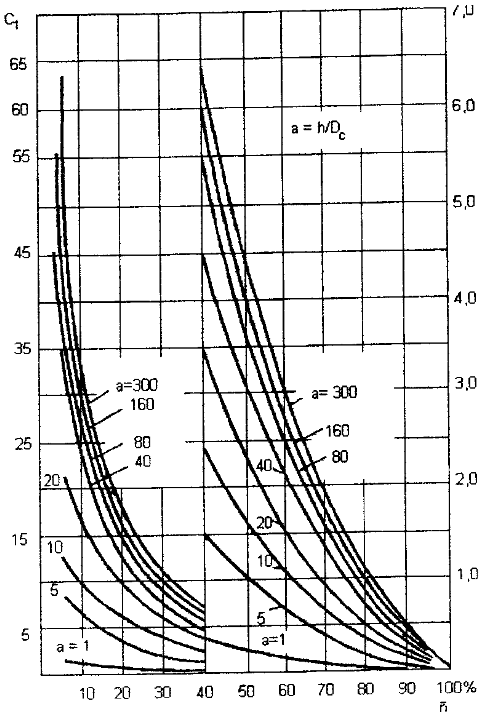 Рисунок 4 - График для определения поправки 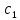 на несовершенство скважины по степени вскрытия на несовершенство скважины по степени вскрытияНа рисунке 5 дана зависимость 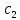 от трех параметров: от трех параметров: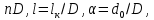 где n - число перфорационных отверстий на 1 м; D - диаметр скважины в м; 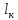 - средняя глубина перфорационного канала в м; - средняя глубина перфорационного канала в м;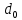 - средний диаметр перфорационных отверстий в м. - средний диаметр перфорационных отверстий в м.Соответствие между кривыми и значениями параметра 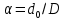 видно из следующих данных: видно из следующих данных:
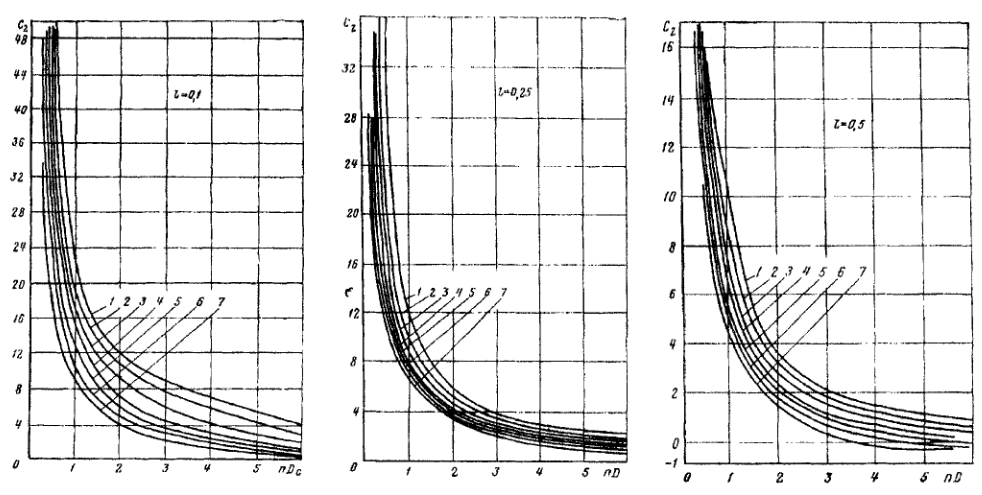 Рисунок 5 - График для определения поправки 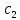 на несовершенство скважины по характеру вскрытия для различных значений на несовершенство скважины по характеру вскрытия для различных значений 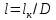 При решении задач на ЭВМ графические зависимости Щурова становятся непригодными, так как они ограничены количеством представленных зависимостей для параметра a и недостаточной точностью графического определения. Поэтому для разработки программных продуктов на ЭВМ требуются аналитические решения. Аналитические методы Формула М. Маскета. Учет несовершенства скважины по степени вскрытия С1 В случае гидродинамически несовершенной скважины по степени вскрытия дебит скважины может быть определен формулой М. Маскета (6), полученной в ходе подбора интенсивности расходов и использовании метода суперпозиции действительных и отображённых стоков: 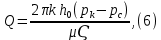 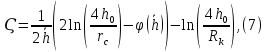 Q - объемный дебит жидкости, м3/с; (pk – pc) — депрессия, Па; µ — вязкость, Па∙с; k — коэффициент проницаемости, м2; h0 — толщина пласта, м; 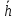 — относительное вскрытие пласта, д.ед.; — относительное вскрытие пласта, д.ед.; Rк — радиус контура питания, м. Функция 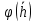 выражается следующей формулой (8): выражается следующей формулой (8):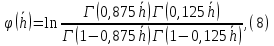 где Г(х) — гамма-функция Эйлера (см. Приложение 2). Формула М.Маскета (6) дает хорошие результаты, при не слишком малом относительном вскрытии, а так как она проще остальных формул, то ею обычно и пользуются для скважин, несовершенных по степени вскрытия, но совершенных по характеру вскрытия. В формуле М. Маскета используется сложная функция 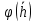 , которая содержит в себе логарифмическую зависимость и гамма-функцию Эйлера. Поэтому часто для получения значения , которая содержит в себе логарифмическую зависимость и гамма-функцию Эйлера. Поэтому часто для получения значения 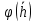 пользуются не расчетной формулой, а графической зависимостью, точность которой ограничена. Формула М. Маскета была получена для условия, что радиус контура питания пласта Rк, больше его мощности. В этом случае формула дает достаточно хорошие результаты. Формулой М. Маскета можно пользоваться и когда радиус контура питания R0 меньше толщины пласта, до соотношения ℎ0/2 ≤ 𝑅к. Но в этом случае формула Маскета будет давать менее точные результаты. пользуются не расчетной формулой, а графической зависимостью, точность которой ограничена. Формула М. Маскета была получена для условия, что радиус контура питания пласта Rк, больше его мощности. В этом случае формула дает достаточно хорошие результаты. Формулой М. Маскета можно пользоваться и когда радиус контура питания R0 меньше толщины пласта, до соотношения ℎ0/2 ≤ 𝑅к. Но в этом случае формула Маскета будет давать менее точные результаты.Определение коэффициента несовершенства скважины по степени вскрытия С1 Опираясь на исследования М. Маскета, И.А. Чарный получил формулу (9) для коэффициента С1, которая включает в себя зависимость от гамма функции Эйлера 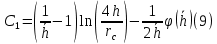 Для определения коэффициента С1 А.М. Пирвердян предложил следующее выражение (10): 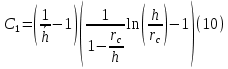 А Г.Б. Пыхачев предложил следующую формулу (11): 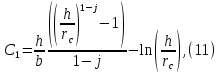 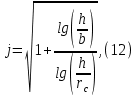 где b = h ⋅ 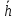 — вскрытие пласта, м. — вскрытие пласта, м.Н.С. Благонравовым и Т.Г. Степаненко произведена сравнительная оценка коэффициента фильтрационного сопротивления С1, обусловленного несовершенством по степени вскрытия при линейном законе фильтрации для однородно-изотропного пласта, и приведена в работе Г.Б. Пыхачева. В широком диапазоне сравнивались численные значения полученные по приближенным формулам Пирвердяна и Пыхачева с экспериментальными данными Щурова. Сравнительный анализ показал, что формула Пирвердяна дает завышение значения С1, а формула Пыхачева достаточно близка к результатам метода ЭГДА. Следует отметить, что эти формулы не учитывают анизотропию пласта, а зависят только от толщины пласта, относительного вскрытия, и радиуса скважины. Аналитическое решение значения С1 с учетом анизотропии пласта получено Ю. И. Сткляниным и А. П. Телковым (13): 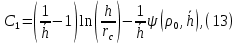 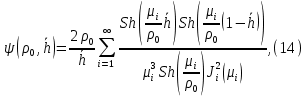 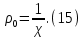 Второе слагаемое формулы Стклянина-Телкова (13) содержит в себе сложную функцию 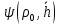 от параметра ρ0, обратнопропорционального анизотропии и относительного вскрытия, и вычисляется с помощью гиперболического синуса и специальных Бесселевых функций первого рода нулевого и первого порядка. Значения функции от параметра ρ0, обратнопропорционального анизотропии и относительного вскрытия, и вычисляется с помощью гиперболического синуса и специальных Бесселевых функций первого рода нулевого и первого порядка. Значения функции 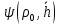 затабулированы авторами в широком диапазоне параметров 0,1 ≤ ρ0 ≥ 100; 0,1 ≤ затабулированы авторами в широком диапазоне параметров 0,1 ≤ ρ0 ≥ 100; 0,1 ≤ 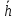 ≥ 0,9. ≥ 0,9. М.Н Велиев исследовал гидродинамические задачи притока жидкости к вертикальной скважине, которая вскрыла толщину продуктивного пласта в произвольном интервале. Целью исследования являлось получение аналитических выражений для коэффициентов дополнительных фильтрационных сопротивлений, на основании которых можно было бы составить алгоритмы решаемой задачи и машинные программы для использования их при проведении вычислительной работы на компьютерах. В результате получена приближенная формула для определения коэффициента С1, учитывающего анизотропию пласта:  Определение коэффициента несовершенства скважины по степени вскрытия С1 и с учетом гидродинамического несовершенства С2, вызванного перфорацией Наиболее практически приемлемым для дебита перфорированной скважины является решение, полученное Е.Б Соловкиным и Н.А. Соловкиной на основе исследованиях Ю.П. Борисова, В.П. Пилатовского и В.П. Табакова: 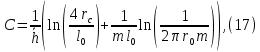 где l0 — длина перфорационного канала, м; r0 — радиус перфорационного отверстия, м; m — плотность перфорации, отв./м. Формула (17) справедлива для любой схемы вскрытия при условии, что каждый из перфорационных каналов ограничен горизонтальными плоскостями с одинаковыми расстояниями между отверстиями и плоскостями. В общем случае, когда скважина несовершенна и по степени, и по характеру вскрытия совокупный скин-фактор можно определить по формуле (18): 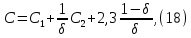 где δ – относительное вскрытие пласта (доля вскрытой части пласта b в его общей толщине h). Коэффициенты С1 и С2 можно определить по аппроксимирующим графики В.И. Щурова формулам, полученным А.А. Мордвиновым (19-20): 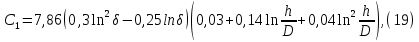 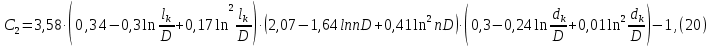 где D – диаметр скважины; lк – глубина перфорационных каналов; n – плотность перфорации (количество перфорационных отверстий, приходящееся на единицу вскрытой толщины пласта); dк (dо) – диаметр перфорационных каналов. |
