Вычисление координат пунктов теодолитных ходов производят в ведо. Исходные геодезические данные
 Скачать 280.5 Kb. Скачать 280.5 Kb.
|
|
Вычисление координат пунктов теодолитных ходов производят в ведомости координат, куда вписывают измеренные углы, горизонтальные проложения, координаты исходных геодезических пунктов. Исходные данные для выполнения математической обработки были получены в результате полевых работ и состоят из геодезических данных и абриса земельного участка. Исходная геодезическая основа была занесена в таблицу 1 и состоит из дирекционных углов, измеренных длин линий и координат начальной точки. Таблица 1 – Исходные геодезические данные
Абрисом называется схематический рисунок участка с натуры, содержащий изображение его границ. Абрис земельного участка, полученный в результате полевых работ, изображен на рисунке 1. 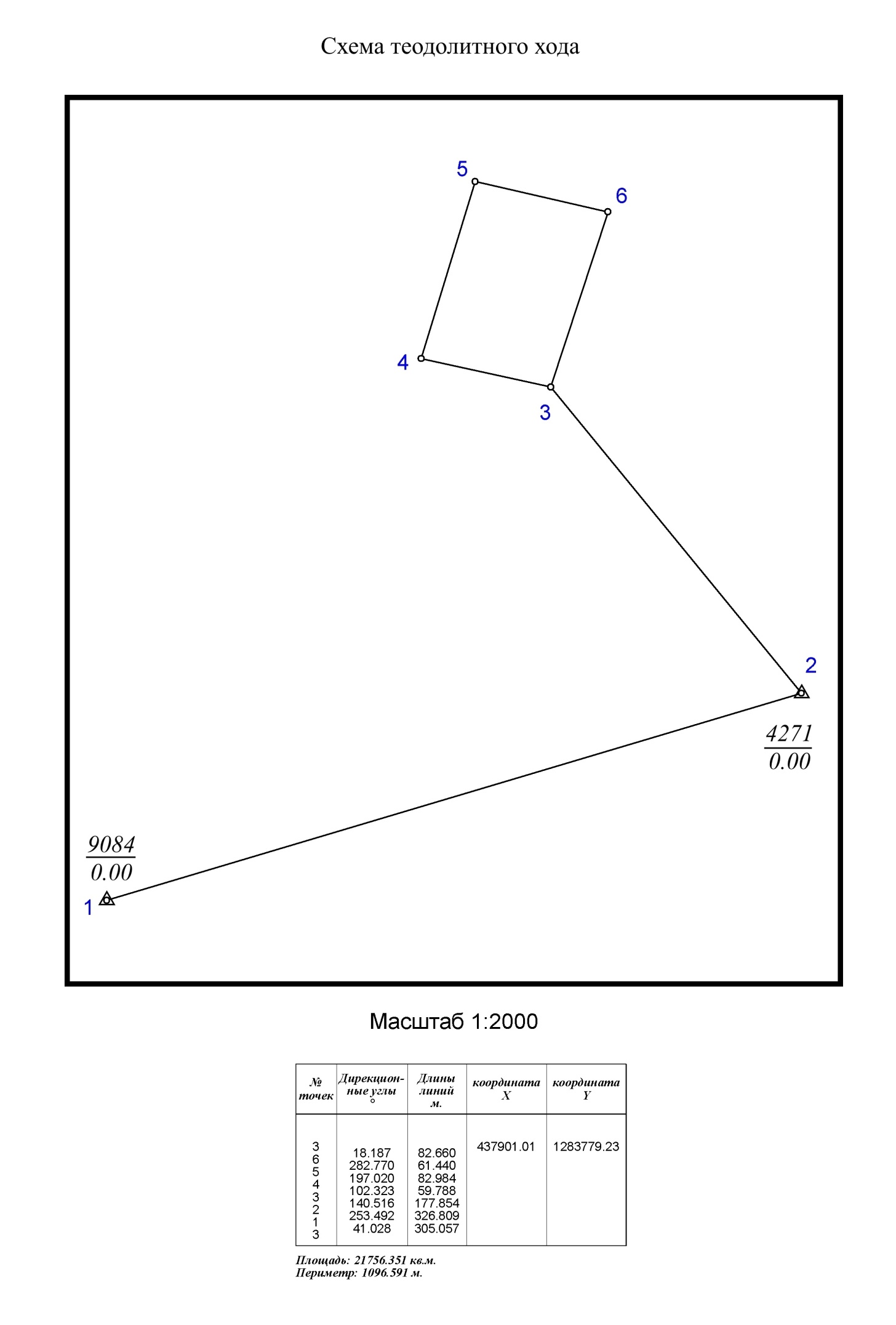 Рисунок 1 – Абрис земельного участка. 3.1 Определение периметра, вычисление румбов Определяем периметр земельного участка по формуле Р = ∑ Di(1) где Р – периметр хода; Di – горизонтальное проложение между точками. Р=82,660+61,440+82,984+59,788+177,854+326,809+305,057=1096,591 м. Определяем последовательно румбы углов межевых знаков. Последовательное вычисление дирекционных углов заканчиваем получением точного значения исходного дирекционного угла. Зависимость между дирекционными углами и румбами в каждой четверти приведена на рисунке 2. 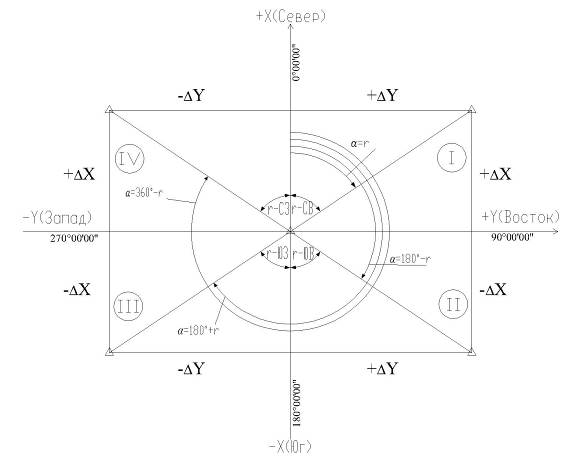 Рисунок 2 – Зависимость между дирекционными углами и румбами. В таблице 2 приведены формулы зависимости между дирекционными углами и румбами Таблица 2 – Зависимость между дирекционными углами и румбами
Названия румбов и их численные значения вписываем в графы 2 и 3 в таблице 3. В таблице 3 представлены вычисленные румбы межевых знаков Таблица 3 – Вычисленные румбы межевых знаков
Вычисление приращений координат выполняется по следующим формулам: ∆Хi = Di х cos ri(2) ∆Yi= Di х sin ri. где ∆Хi– приращение координат по оси Х; ∆Уi– приращение координат по оси У; Di – горизонтальное проложение между точками (длина); ri – румб этой линии. Приращения координат вычисляются с точностью до двух знаков после запятой. Вычисляем приращения координат по оси Х ∆Х1-2 = D×cos1-2=0,9500*82,660=78,53+ ∆Х 2 = 0,2210*61,440=13,58+ ∆Х 3= 0,9562*82,984=79,35- ∆Х 4= 0,2134*59,788=12,76- ∆Х 5 =0,7718*177,854=137,27- ∆Х 6 = 0,2841*326,809=92,85- ∆Х 7 = 0,7544*305,057=230,13+ Вычисляем приращения координат по оси У ∆Y1 =0,3121*82,660=25,80+ ∆Y2 =0,9753*61,440=59,92 - ∆Y3 = 0,2927*82,984=24,29- ∆Y4 = 0,9769*59,788=58,41+ ∆Y5 = 0,6359*177,854=113.1+ ∆Y 6 = 0,9588*326,809=313,34- ∆Y 7 = 0,6564*305,057=200,24+ Контроль вычислений осуществляем по следующей формуле ∆Yi= tgr х∆Хi (3) где ∆Уi– приращение координат по оси У; ∆Хi– приращение координат по оси Х; ri – румб линии. ∆Y 1 = tg 18°11'13" х78,527= 0,3285 х78,527 = 25,7971 ∆Y 2 = tg 77°13'48"x13,58 =4,4122 x 13,58 =59,9177 ∆Y 3 = tg” 17°01'12" x 79,349=0,3061 x 79,35 =24,2890 ∆Y4 = tg77°40'37" x12,759 =4,5776 x 12,76 =58,4102 ∆Y 5 = tg39°29'02" x 137,268 =0,8234 x 137,27 =113,0281 ∆Y6 = tg73°29'31" x 92,846=3,3742 x 92,85 =313,2944 ∆Y7 = tg 41°01'41"x230,135 =0,8701 x 230,13 =200,2361 ∆X 1 = tg 18°11'13" х25,798= 0,3285 х25,798= 8.4746 ∆X 2 = tg 77°13'48"x59,922 =4,4122 x59,922 =264.3878 ∆X 3 = tg” 17°01'12" x 24,289=0,3061 x24,289 =7.4349 ∆X4 = tg77°40'37" x58,406=4,5776x58,406=267.3593 ∆X 5 = tg39°29'02" x 113.097=0,8234 x113.097 =93,1241 ∆X6 = tg73°29'31" x 313,344=3,3742 x313,344 =1057,2853 ∆X7 = tg 41°01'41"x200,239=0,8701 x 200,239=174,2279 ∆Y1 = 25,798 ≈ 25,7971 ∆Y2 = 59,922 ≈ 59,9177 ∆Y3 = 24,2890≈ 24,2890 ∆Y4 = 58,406≈ 58,4102 ∆Y5 =113.097 ≈113,0281 ∆Y 6 = 313,324≈313,2944 ∆Y 7 = 200,239≈200,2361 Погрешности вычислений допустимы. Далее в таблице 3 приводится схема, по которой определяются знаки приращений по осям координат в соответствии со значениями румбов. Таблица 3 - Определение знаков приращений
3.2 Построение плана теодолитного хода Сумма проекций сторон (приращений координат) замкнутого теодолитного хода на соответствующие координатные оси должна равняться нулю, как это видно из формулы 2: (4) Σ∆Х = 0 Σ∆Y= 0 Однако на практике, в связи с погрешностями линейных измерений, Σ∆Х иΣ∆Yравны некоторым величинам 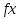 и и 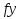 , называемые линейными невязками в приращениях координат: , называемые линейными невязками в приращениях координат: 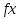 – по оси абсцисс и – по оси абсцисс и 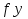 – по оси ординат. – по оси ординат. Подсчет линейной невязки 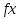 и и 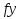 приращения координат по осям, вычисляется по формулам приращения координат по осям, вычисляется по формулам fх = Σ Δ х i (5) fу = Σ Δ у i где Σ Δ х i –сумма приращенийпо оси Х; Σ Δ у i - сумма приращенийпо оси У. Но из-за неизбежных случайных погрешностей, допускаемых при измерении длин линий, эти соотношения обычно не выполняются. В большинстве случаев алгебраические суммы приращений не будут равны нулю, а равняются некоторым величинам: Эти величины, называемые невязками приращений координат, являются проекциями линейной невязки хода на оси координат: 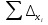 = 78.527+13.578-79.349-12.759-137.268-92.846+230.135=+0.018 = 78.527+13.578-79.349-12.759-137.268-92.846+230.135=+0.018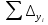 = 25.798-59.922-24.289+58.406+113.097-313.344+200.239=-0.015 = 25.798-59.922-24.289+58.406+113.097-313.344+200.239=-0.015В результате неизбежных ошибок измерений замкнутый полигон оказывается как бы разомкнутым на величину 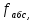 называемую невязкой в периметре полигона. называемую невязкой в периметре полигона. Абсолютная невязка определяется по формуле и является критерием точности измерения длин линий. Она не должна превышать 1/2000 доли периметра хода. 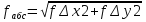 (6) (6)где fΔх2 - квадрат линейной невязки по оси Х; fΔу2 - квадрат линейной невязки по оси У 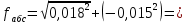 0,009 0,009Чтобы убедиться в этом, подсчитывают относительную невязку 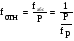 (7) (7)где Р – периметр хода; fабс – абсолютная невязка; f p – Относительная невязка не должна превышать 1/2000 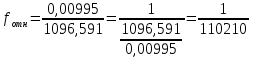 Относительная невязка 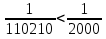 В случае невыполнения этого условия проверяют записи в журнал и правильность вычислений. Если при этом ошибка не будет обнаружена, то выполняют полевые контрольные измерения. Если относительная невязка периметра полигона не превышает допустимую, производят уравнивание приращений координат. Простейший способ уравнивания заключается в распределении невязок в приращениях координат между соответствующими прращениями пропорционально длинам сторон со знаком, обратным знаку невязки. Невязка допустимая. Она распределяется по углам с обратным знаком, с округлением дробных значений минут до целых. Значения исправленных углов заносятся в графу три ведомости координат. Распределение невязки приращений координат в вычисленные приращения. Поправки в приращения координат распределяются пропорционально длинам сторон теодолитного хода по каждой из осей (берутся в сотнях метров). Знак поправки противоположен знаку невязки. Контроль распределения поправок - сумма поправок должна быть равна невязке с противоположным знаком. Проложение и периметр берутся в сотнях метров. Рассчитывается по формулам: δ Δхi = f Δхi / Р D i (8) δΔуi =f Δ уi/ Р Di где f Δхi– приращение координатпо оси Х; f Δ уi– приращение координат по оси Y; Di – горизонтальное проложение между точками (длина); Р – периметр хода δ Δх = 0,018/10,9659 х Di = 0,00164х D i δ Δу =-0,015 / 10,9659х Di = - 0,00137х D i δ Δх1 = 0,00164х 0,8266 = 0,0013556 δ Δу1 = -0,00137х 0,82660 = -0,0011324 δ Δх2 = 0,00164х 0,61440 = 0,0010076 δ Δу2= -0,00137х0,61440 = -0,0008417 δ Δх3 =0,00164 х 0,82984 = 0,0013609 δ Δу3 = -0,001378х 0,82984 =- 0,0011368 δ Δх4 = 0,00164х0, 59788 =0,0009805 δ Δу4 = - 0,00137х 0,59788 =-0,0008191 δ Δх5 = 0,00164 х 1,77854 = 0,0029168 δ Δу5 = -0,00137х 1,77854= -0,0024366 δ Δх6 = 0,00164х 3,26809= 0,0053596 δ Δу6 = -0,00137х 3,26809= -0,0044773 δ Δх7 = 0,00164х 3,05057 = 0,0050029 δ Δу7 = -0,00137х 3,05057 =-0,0041793 Контроль : Σ υ Δх = = 0,0013556+0,0010076 +0,0013609+0,0009805+0,0050029 +0,0053596+0,0029168=0,018 Σ υ Δу = 0,0011324+0,0008417+0,0011368+0,008191+0,0024366+0,0044773+0,0041793= -0,015 Знаки поправок противоположны знакам невязок. При вычислениях поправок в формулы подставляются величины периметра Р и горизонтальных проложений Di , округленные до целых метров. Величины поправок, округленные до 0,01 м, записываются над соответствующими приращениями. Следует убедиться, что сумма всех поправок в каждой графе равна величине невязки fx или fy с противоположным знаком. Если равенства нет, поправки, соответствующие самым длинным линиям, увеличиваются. Приращения исправленные находят как алгебраическую сумму приращения вычисленного и поправки к нему. Исправленные значения приращений координат с учетом поправок будут иметь следующий вид и рассчитываются по формулам: ∆Хiисп = ∆Хi ± υ(9) ∆Yi исп = ∆Yi ± υΔуi ∆Х1 исп = + 78,527+ 0,0013556= +78,53 ∆Х2исп = + 13,578+0,0010076=+13,58 ∆Х3 исп =- 79,349+ 0,0013609= -79,35 ∆Х4 исп =-12,759+0,0009805= -12,76 ∆Х5 исп = -137,268+0,002916 = -137,29 ∆Х6 исп = -92,846+0,0053596= -92,85 ∆Х7 исп = +230,135+ 0,0050029 =+230,14 ∆Y1 исп = + 25,798 - 0,0011324 =25,79 ∆Y2 исп = -59,922-0,0008417=-59,92 ∆Y3 исп = -24,289- 0,0011368=-24,26 ∆Y4 исп = +58,406 -0,0008191=58,40 ∆Y5 исп = +113,097-0,0024366=113,09 ∆Y6 исп = -313,344-0,0044773=-313,35 ∆Y7 исп = +200,239 -0,0041793=200,25 После введения поправок к соответствующим приращениям координат суммы исправленных приращений должны равняться нулю Σ∆Хисп = 0 (10) Σ∆Yисп = 0 Контроль: Σ ∆Х = 78,53+13,58 +(-79,35)+230,14+(-137,29)+( -92,85)+(-12,76)=0 Σ ∆Y =25,79+(-59,92)+(-24,26)+58,40+200,25+(-313,35)+113,09=0 Вычисление координат межевых знаков полигона по формулам: X послед. = X пред ± ∆ x (11) Y послед. = Y пред ± ∆y Х 2 = 437901,01+78,53= 437979,54м Х 3= 437979,54+13,58= 437993,12м Х 4=437993,12- 79,25= 437913,77м Х 5= 437913,77- 12,76= 437901,01м Х 6 =437901,01-137,29= 437763,72 м Х 7 = 437763,72- 92,85=437670,87 м Х 8 = 437670,87 + 230,14= 437901,01м Контроль : 442414,630 ≈ 442414,630 Y 2 = 1283779,23+25,79=1283805,03м Y 3= 1283805,03-59,92= 1283745,11м Y 4 = 1283745,11+24,26= 1283720,82м Y 5 = 1283720,82+58,40= 1283779,23м Y 6 = 1283779,23+113,09= 1283892,32м Y 7 = 1283892,32- 313,09= 1283579м Y 8 = 1283579+200,25= 1283779,23м Контроль: 1282270,960 ≈ 1282270,960 Все данные по вычислению координат межевых знаков теодолитного хода вносятся в итоговую ведомость и показаны в таблице 4. Построение плана снятого участка производится в масштабе 1:1000 на чертежной бумаге формата А2 в определенной последовательности: 1) построение координатной сетки (сетки квадратов) со сторонами 10 × 10; 2) нанесение вершин теодолитного хода по координатам; 3) нанесение на план ситуации по абрисам; 4) оформление плана. Координатную сетку строят при помощи линейки. Построение и оцифровку линий координатной сетки производят с таким расчетом, чтобы построенный по координатам теодолитный план оказался симметричным краям листа бумаги. Ниже оформляют ведомость координат теодолитного хода. Таблица 4 - Ведомость
3.3 Определение площади земельного участка аналитическим способом Определяем площадь земельного участка аналитическим способом (по координатам) Координаты вершин полигона: Ось знак значение Х3 + 437901,01 Х6 + 437979,54 Х5 + 437993,12 Х4 + 437913,77 Х3 + 437670,87 Х2 + 437763,72 Х1 + 437901,01 Ось знак значение У3 + 1283779,23 У6 + 1283805,03 У5 + 1283745,11 У4 + 1283720,82 У3 + 1283779,23 У2 + 1283892,32 У1 + 1283579 У3 + 1283779,23 Сделать последовательно для иксов и игреков Площадь полигона определяется по следующим формулам: 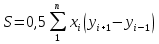 (10) (10)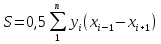 (11) (11)где n – число поворотных точек; i принимает значения от 1 до n Определяем разности координат, придавая значения i от 1 до n У3 - у2 = 1283779,23-1283892,32=-113,09 У1- у3= 1283579-1283779,23=-200,23 У2- у4 = 1283892,32-1283720,82=171,5 У3- у5 = 1283779,23-1283745,11=34,12 У4- у6= 1283720,82-1283805,03=-84,23 У5- у3= 1283745,11-1283779,23=-34,14 У6- у1= 1283805,03-1283579=226,03 Контроль Х2- х3 = 437763,721-437901,01=-137,29 Х3- х1= 437901,01-437670,885=+230,14 Х4- х2 = 437913,766-437763,721=150,05 Х5- х3 = 437993,115-437901,01=92,11 Х6- х4= 437979,537-437913,766=65,77 Х3- х5= 437901,01-437993,115=-92,11 Х1- х6= 437670,885-437979,537=-308,67 Контроль Определяем произведения: хi(уi+1 х уi-1) х1 (у2 - у3) = 437670,87*(-113,09)= -49496198,68 х2 (у3- у1) = 437763,72*(-200,23)= -8763285,49 х3 (у4- у2) = 437901,01*171,5= 75100023,21 х4 (у5- у3) = 437913,77*34,14= 14950376,11 х5 (у6- у4) = 437993,12*(-84,23)= -36892160,49 х6 (у7- у5) = 437979,54*(-34,12)= -14943861,90 х7 (у8- у6) = 437901,01*226,03= 98978765,29 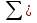 43515,48 43515,48уi(хi+1 х хi-1) у1 (х2- х8) = 1283579*(-137,289)=-176221277,331 у2 (х1- х3) = 1283892,32*230,125=295455720,14 у3 (х2- х4) = 1283779,23*150,045=192624654,565 у4 (х3- х5) = 1283720,82*92,105=118237106,126 у5 (х4- х6)= 1283745,11*65,771=84433199,629 у6 (х5- х7) = 12838805,03*(-92,105)=-1182515137,28815 у7 (х6- х8) = 12838779,23*(-308,652)=-3962714886,897 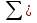 43519,522 43519,522Определяем площадь полигона 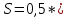 43515,48= 21757,74 43515,48= 21757,74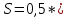 43519,522= 21759,76 43519,522= 21759,76Все данные вносим в ведомость вычисления площади земельного участка Таблица 5 - Координаты
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

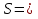 Ѕ=21757,74
Ѕ=21757,74