Курсовая Использование аттракторов. Использование аттракторов
 Скачать 367.67 Kb. Скачать 367.67 Kb.
|
Аттрактор ЛоренцаАттрактор Лоренца ― компактное инвариантное множество L в трехмерном фазовом пространстве гладкого потока, которое имеет определённую сложную топологическую структуру и является асимптотически устойчивым, оно устойчиво по Ляпунову и все траектории из некоторой окрестности L стремятся к L при t → ∞(отсюда название). Аттрактор Лоренца был найден в его численных эксперимента, исследовавшего поведение траекторий нелинейной системы: 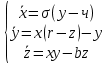 при следующих значениях параметров: σ=10, r=28, b=8/3, x(0)=1, y(0)=0, z(0)=0. Эта система изначально была введена как первое нетривиальное галёркинское приближение для задачи о конвекции морской воды в плоском слое, чем и мотивировался выбор значений σ, r иb, но она возникает также и в других физических вопросах и моделях: конвекция в замкнутой петле; вращение водяного колеса; модель одномодового лазера; диссипативный гармонический осциллятор с инерционной нелинейностью. Исходная гидродинамическая система уравнений: 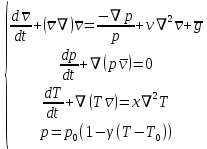 Где 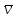 — скорость течения, T — температура жидкости, — скорость течения, T — температура жидкости, 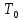 — температура верхней границы (на нижней поддерживается — температура верхней границы (на нижней поддерживается 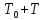 , , 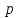 — плотность, — плотность, 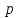 — давление, — давление, 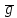 — сила тяжести, — сила тяжести,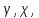 υ— соответственно коэффициент теплового расширения, коэффициент температуропроводности и кинематической вязкости. υ— соответственно коэффициент теплового расширения, коэффициент температуропроводности и кинематической вязкости.В задаче о конвекции модель обнаруживается при разложении скорости течения и температуры в двумерные ряды Фурье и дальнейшей их «обрезки» с точностью до первых-вторых гармоник. Кроме того, приведённая полная система уравнений гидродинамики записана в приближении Буссинеска. Обрезка рядов умеренно оправдана, так как Сольцмен в своих работах показал отсутствие каких-либо интересных особенностей в поведении большинства гармоник. 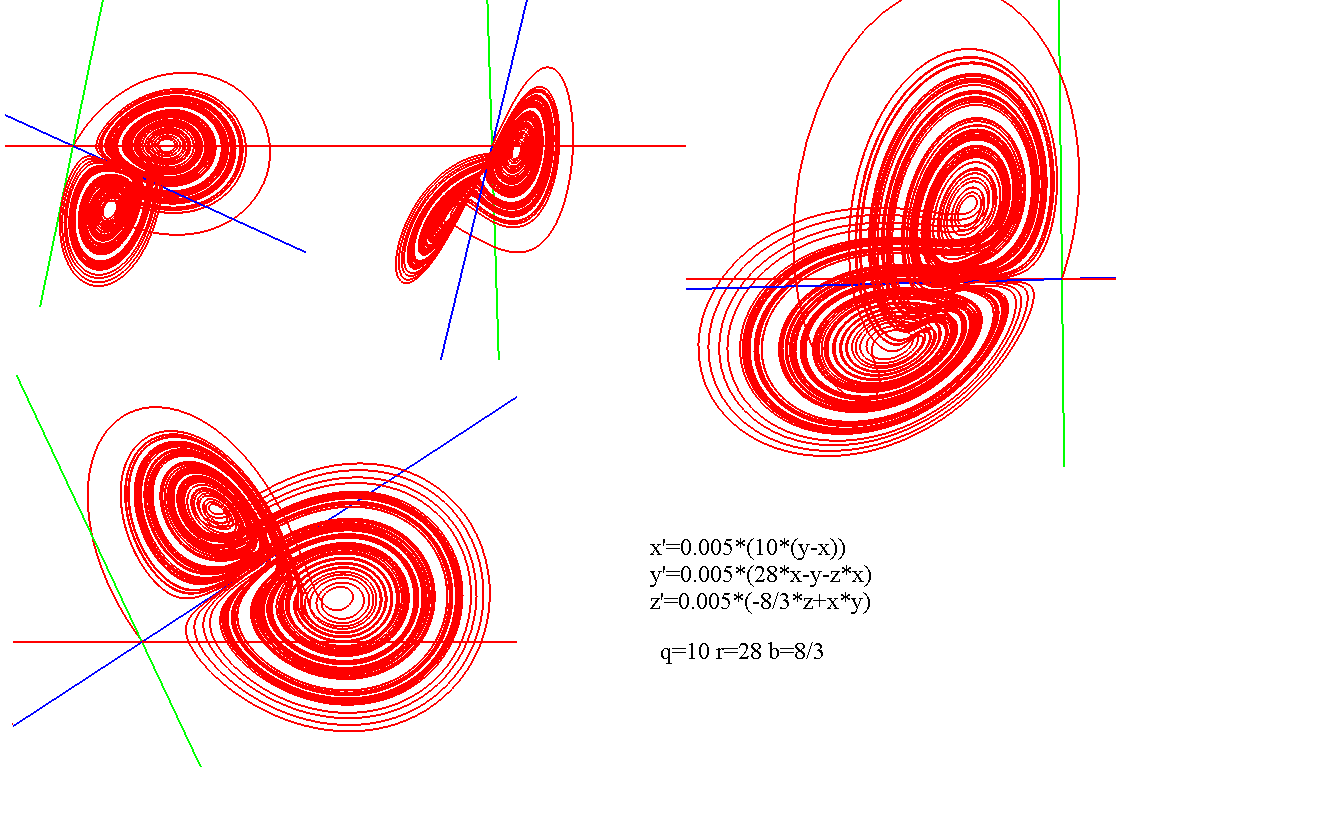 Осциллятор Ван дер ПоляОсциллятор Ван дер Поля — осциллятор с нелинейным затуханием, подчиняющийся уравнению 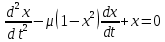 , где , где Х — координата точки, зависящая от времени t; μ — коэффициент, характеризующий нелинейность и силу затухания колебаний. Двумерный случай Следуя теореме Льенара можно доказать, что система имеет предельный цикл. Из данной теоремы следует, 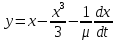 . Отсюда можно вывести уравнения осциллятора Ван дер Поля для двумерного случая: . Отсюда можно вывести уравнения осциллятора Ван дер Поля для двумерного случая: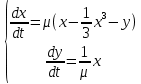 Кроме этого можно совершить другую замену 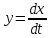 и получить и получить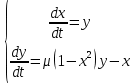 Осциллятор со свободными колебаниями У осциллятора Ван дер Поля существуют два интересных режима: при 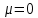 и при и при 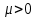 Стоит отметить, что третьего режима — Стоит отметить, что третьего режима — 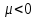 — не существует, поскольку затухание в системе не может быть отрицательным. — не существует, поскольку затухание в системе не может быть отрицательным.Когда 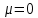 , то есть осциллятор рассчитывается без затухания, то указанные выше уравнения преобразуются к видy , то есть осциллятор рассчитывается без затухания, то указанные выше уравнения преобразуются к видy 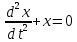 . .Это уравнение гармонического осциллятора. 2) При 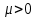 система имеет определенные предельные циклы. Чем дальше система имеет определенные предельные циклы. Чем дальше 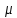 от нуля, тем колебания осциллятора менее похожи на гармонические. от нуля, тем колебания осциллятора менее похожи на гармонические.Вынужденные колебания Вынужденные колебания осциллятора Ван дер Поля как с потерями энергии, так и без оных рассчитываются по формуле 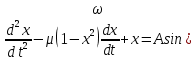 t), где t), где А — амплитуда внешнего гармонического сигнала, 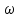 — его угловая частота. — его угловая частота.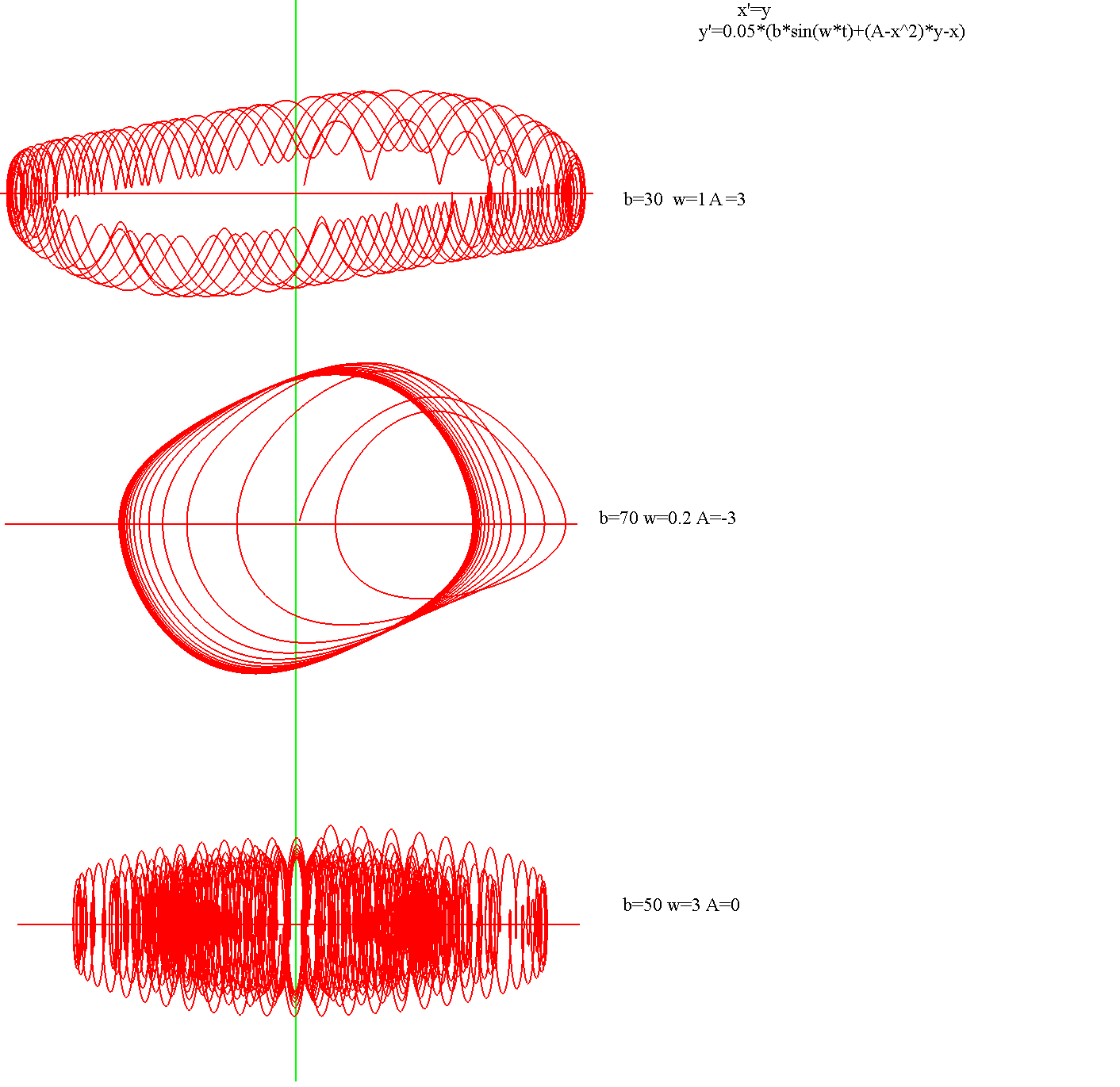 |
