Использование фрактального анализа для оценки механизмов адаптац. Использование фрактального анализа для оценки механизмов формирования адаптаций у растений в естественных условиях
 Скачать 95.8 Kb. Скачать 95.8 Kb.
|
|
УДК 57.022 Использование фрактального анализа для оценки механизмов формирования адаптаций у растений в естественных условиях Щербаков А.В. Институт генетических и тканевых исследований (ИГИТИ), Уфа Показана возможность применения фрактального анализа для изучения спектров отдельных адаптивных механизмов, запускаемых растениями в ответ на те, или иные комбинации факторов внешней среды. Ключевые слова: фрактальный анализ, условия обитания, стресс, многомерная экологическая ниша, морфофизиологические параметры флавоноиды, корреляционные связи. Введение Высокая вариативность отдельных экологических факторов является одним из основных свойств естественной среды обитания растений. Например, в почвах взаимное влияние на накопление и распределение химических элементов имеет очень сложную, а в условиях Зауралья – и многоуровневую, природу, что дало основание для введения термина «многомерная экологическая ниша». В различных работах было показано, что в этом регионе локальное содержание отдельных элементов может варьировать от серьезного дефицита до токсического избытка. На фоне этого у растений формируется очень сложная картина запускаемых ответных адаптивных механизмов. Работа этих механизмов у индивидуальных растений может быть отслежена по широкому спектру морфологических и физиологических показателей. Однако коррелляционный анализ показывает, что в естественных местообитаниях картина корреляционных связей между отдельными индивидуальными показателями растений чрезвычайно нестабильна, как в пространстве, так и во времени. Это как раз и свидетельствует о высокой пластичности формируемых у растений в естественных местообитаниях спектров отдельных адаптивных механизмов. В ряде работ было показано, что такая пластичность является ответной реакцией на высокую вариабельность и непредсказуемость их среды обитания. При этом остаются неясными некоторые вопросы, касающиеся общих принципов формирования адаптивных реакций у отдельных растений: Как связаны локальные сочетания показателей внешней среды со спектром запускаемых отдельным растением индивидуальных адаптивных механизмов? От чего вообще зависят индивидуальные спектры запущенных растениями адаптивных механизмов ? В том случае, если для успешного преодоления какого либо стресса растения запускают нескольких альтернативных механизмов, как формируется соотношение между этими механизмами? Является ли оно случайным, или наоборот, жестко детерминированным? Насколько схожи индивидуальные спектры работающих адаптивных механизмов у растений, находящихся в одинаковых условиях, и как меняется картина этих механизмов в зависимости от уровня рассмотрения? Существует ли единая теория, позволяющая предсказать адаптивный ответ отдельных растений на то или иное воздействие, подобно теории рефлексов И.П. Павлова? Имеются ли в адаптивном поведении растений элементы самоподобия? В настоящее время в науках о Земле все большее применение находит фрактальный подход (Гелашвили и др., 2013). Особенно серьезный прогресс в применении фрактальной логики наблюдается в экологии и некоторых разделах биологии. Доказано, что фрактальные свойства характерны для очень широкого перечня природных объектов (рис.1): 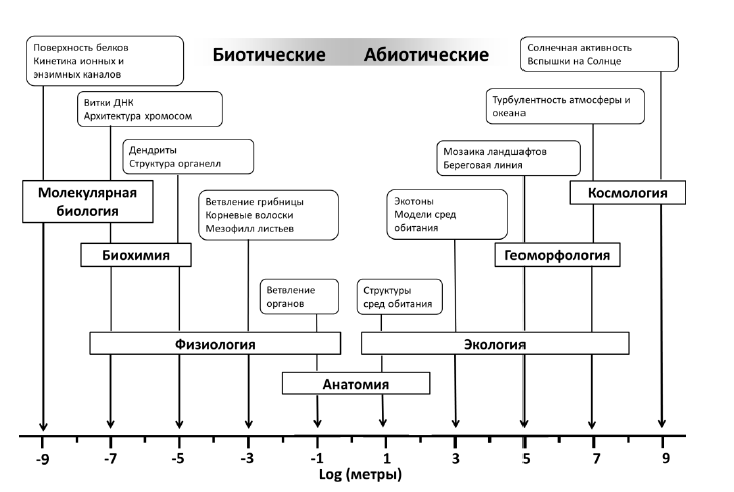 Рисунок 1. Фрактальные свойства природных обьектов и процессов (цит. По Гелашвили и др., 2013). Также установлено, что фрактальными свойствами могут обладать не только фиксированные структуры, но и динамические процессы, при этом основными критериями соответствия объекта фрактальной природе является многоуровневый характер этого объекта и наличие самоподобия в широком диапазоне уровней и во временной перспективе. Все вышеперечисленное позволило считать целесообразным применение метода фрактального анализа в физиологии растений, а именно - при изучении адаптивного ответа растений на внешние условия в естественных местообитаниях. Многоуровневость растительных сообществ, не вызывает сомнений: объектами изучения могут служить индивидуальные растения, группы растений произвольного размера, отдельные популяции, целый вид). Поэтому для доказательства фрактальной природы адаптивного поведения растений в принципе достаточно доказать его самоподобие в широком диапазоне выбранных уровней. Теоретические подходы и возможная интерпретация результатов Условно любые многокомпонентные системы по своим свойствам могут быть отнесены к одному из трех классов, четкой границы между которыми не существует. Объекты регулярной природы Фрактальные объекты Объекты преимущественно хаотические ( таб. 1) Таблица 1. Основные свойства регулярных, фрактальных и хаотических обьектов
Описанная в литературе (Гелашвили и др., 2013) и адаптированная нами под задачи физиологии растений методика фрактального анализа позволяет проверять на самоподобие любые массивы индивидуальных данных, как растений, так, например, и почвенных образцов. При этом в расчетах могут быть использованы любые индивидуальные данные – ростовые и морфологические показатели, содержание отдельных метаболитов (в том числе - и вторичных), локальные почвенные показатели. Минимальный размер массива данных должен быть не менее 10*10 (10 индивидуальных объектов и 10 показателей). В результате проведенного анализа объект может быть распределен в одну из вышеперечисленных трех классов. Методика проведения фрактального анализа Расчеты проводятся по методике описанной (Гелашвили и др., 2013) и адаптированной для анализа растительных систем. Для проведения всех необходимых расчетов достаточно функциональных возможностей программных пакетов EXCEL и Statistica. На первом этапе анализа подбираются индивидуальные образцы, и выстраивается общая логика их последующей группировки во все более и более крупные выборки. Это определяет дальнейшую процедуру составления на основе этих данных иерархической матрицы, необходимой для фрактального анализа. Данная процедура сводится к 2 основным действиям: Сэмплинг (sampling) - процесс отбора образцов, цель которого - установление некой унифицированной структуры, проверяемой на свойства самоподобия, т.е. выделение предполагаемой «самоподобной» структуры, лежащей в основе фрактальной иерархии. В нашем случае индивидуальной структурой могут служить любые индивидуальные данные. Основное требование – у каждого образца должны быть зафиксированы одни и те же показатели. Скейлинг (sсaling)– определение меры масштаба и диапазона уровней организации (иерархии), в которых предполагается определять у данной структуры наличие свойств самоподобия, то есть – построение общей логики объединения индивидуальных данных в группы того или иного размера, вплоть до общей генеральной совокупности. На первом этапе на основе построенной иерархии в дальнейшем создана обобщающая иерархическая матрица, где указаны индивидуальные показатели объектов, показатели объектов, объединенные в группы различного масштаба, итоговые обобщенные показатели. Именно эта матрица и служит своего рода имитацией многоуровневости, и именно проверка ее на самоподобие является ключевой для фрактального анализа. На основании данной матрицы высчитываются следующие показатели: N — суммарный объем выборки. Этот показатель варьирует от 1 (единичный образец) до N– (все исследованные образцы) с определенным шагом, соответствующим логике объединения образцов ( скейлингу); pi- индекс разнообразия; то есть доля каждого индивидуального значения в формировании общей итоговой картины; q - порядок момента распределения. Этот показатель находился в рекомендованном авторами диапазоне от -3 до 3 и фактически представляет собой диапазон степеней, в которые следует возводить pi каждого элемента матрицы. Тем самым, с помощью данного показателя задается мера масштаба (диапазон), в котором будет проверяться фрактальная природа исследуемого объекта. Mq- моменты распределения индивидуальных значений по классам; Для расчета данного показателя применяется рекомендованное авторами (Gelashvili e.a., 2013) выражение: Mq(N)= 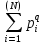 где все показатели описаны выше. На втором этапе для каждого значения q рассчитывается набор моментов распределения Mq (Табл. 2): Таблица 2. Пример наборов моментов распределения Mq, рассчитанных на основе матрицы индивидуальных ВЭЖХ хроматограмм растений Juniperussabina
Свойство самоподобия, считается доказанным в том случае, если во всем диапазоне q наблюдается значимая корреляционная зависимость показателей logMq от logN (Гелашвили с соавт., 2013). Таким образом, доказанное для объекта свойство самоподобия является первым условием соответствия этого объекта принципам фрактального формализма (Табл. 3): Таблица 3. Выявленные значимые корреляционные связи показателей logMq от logN, представленных в таблице 2.
Однако, таким же свойством самоподобия (по мнению авторов методики) могут обладать и объекты регулярной природы, описываемые относительно простыми закономерностями, и в которых между демонстрируемыми показателями на любом уровне всегда существует жесткая функциональная зависимость (все элементы объекта всегда ведут себя одинаково). На третьем этапе несводимость наблюдаемой картины к простым математическим моделям оценивается по информационному критерию Акаике (AIC). Для оценки характера наблюдаемой картины зависимости показателей log Mq от log N авторы методики предлагают применять две модели – линейную и квадратичную. Линейная модель является эталоном объекта регулярной природы. Данный критерий для малых выборок вычислялся по формуле: AIC=ln RSS/n+(n+k)/(n-k-2), где n - объем анализируемых данных, k – число параметров модели (для линейной модели он равен 3, для квадратичной 4), RSS – сумма квадратов отклонений от предсказываемых моделью значений (Гелашвили с соавт., 2013). Критерий Акаике (AIC) рассчитывается для обеих моделей во всем диапазоне использованных в вычислениях значений порядка моментов распределений q. Чем ниже значения этого критерия для каждой из моделей, тем в большей степени она применима для описания зависимости показателей logMq от logN, рассчитанной на основе ранее построенной матрицы. Большая применимость линейной модели во всем диапазоне показателя q свидетельствует о том изучаемый объект имеет регулярную природу ( самоподобие + идентичность свойств индивидуальных обьектов). Наоборот, если хотя бы на каком-нибудь участке диапазона показателя q будет установлена большая применимость квадратической модели, чем линейной, то это будет указывать на возможность обладания изучаемого объекта только свойствами самоподобия и соответственно - фрактальными (мультифрактальными) свойствами. Практика наших исследований показывает, что наиболее часто различия в применимости той или иной модели выявляются в диапазоне q от 0 до 1,5. Таким образом, наличие самоподобия у исследованных образцов оценивается по достоверности линейной зависимости логарифмов показателей N и Mq, а применимость для наблюдаемой картины фрактальной гипотезы – по результатам сравнения критерия Акаике для линейной и квадратической моделей. Полученные результаты и их интерпретация Некоторые результаты проводимого нами фрактального анализа приведены в таблице 4: Таблица 4 Результаты фрактального анализа растительных и почвенных систем
Заключение При значительном ухудшении условий ( стрессе) у растений снижается ресурсное обеспечение. Это приводит к уменьшению у них количества параллельно действующих адаптивных механизмов, возрастанию количества корреляционных связей между параметрами. В этом случае фрактальный анализ описывает группу таких растений, как объект регулярной природы. Литература Гелашвили Д.Б., Иудин Д.И., Розенберг Г.С., Якимов В.Н., Солнцев Л.А. Фракталы и мультифракталы в биоэкологии. Изд. Нижегородского университета, 2013, 370 с. Mandelbrot B.B. The fractal geometry of nature. New York: Freeman, 1982. 468 p. Usmanov I.Yu., Yumagulova E.R., Ovechkina E.S., Ivanov V.B., Shcherbakov A.B., Aleksandrova V.V., Ivanov N.A. Fractal analysis of morpho-physiological parameters of Oxycoccus palustris Pers. in oligotrophic swamps of Western Siberia // Vegetos: An International Journal of Plant Research. 2016. Т. 29. № 1. P. 1-3. 3. Bundy J.G., Davey M.P., Viant M.R. Environmental metabolomics: a critical review and future perspectives. Metabolomics.,2009, 5: 3-21 Усманов И.Ю., Семенова И.Н., Щербаков А.В., Суюндуков Я.Т., Усманов Ю.И. / Эндемичные экологические ниши Южного (Башкирского) Зауралья: многомерность и флуктуирующие режимы. - Уфа: Вестник БГАУ – 2014. - №1. С.16 – 22 Усманов И.Ю., Щербаков А.В., Мавлетова М.В., Юмагулова Э.Р., Иванов В.Б. Пульсирующая многомерная экологическая ниша растений: расширение объема понятия. Известия Самарского Научного центра РАН, 2016, в печати. 3.Щербаков А.В., Мавлетова М.В., Усманов И.Ю., Биктимерова Г.Я. Корреляционные связи параметров почвенной мозаичности и признаков адаптивности растений Южного Зауралья. I. Glycyrrhiza korshinskyi Grig. // Самарская Лука: проблемы региональной и глобальной экологии. Том… №… 2016, С. Щербаков А.В., Мавлетова М.В., Усманов И.Ю., Биктимерова Г.Я. Корреляционные связи параметров почвенной мозаичности и признаков адаптивности растений Южного Зауралья. II. Juniperus sabina l.. Самарская Лука: проблемы региональной и глобальной экологии. Том… №… 2016, С. Игамбердиев А.У. Логика организации живых систем. Воронеж: Издательство воронежского университета, 1995. ‐ 152 с. Шильяк Д. Децентрализованное управление сложными системами. М., Мир, 1994, 575 с. Hans Lambers F. Stuart Chapin III Thijs L. Pons. Plant Physiological Ecology. Second Edition. 2008, Springer Science+Business 623 p. DOI: 10.1007/978-0-387-78341 Rakhmankulova Z.F., Shuyskaya E.V., Suyunducov Ya.T., Usmanov I.Yu., Voronin P.Yu. Different Responses of Two Ecotypes of С3-С4 Xero-halophyte Bassia sedoides to Osmotic and Ionic Factors of Salt Stress. Russian Journal of Plant Physiology, 2016, Vol. 63, No. 3, pp. 229-237. Шпаков А.О. Хемосигнальные системы растений // Цитология, 2009, т. 51, № 9, С. 721 – 734 Усманов И.Ю., Мартынова А.В., Янтурин С.И.Адаптивные стратегии растений на солончаках Южного Урала. Реакция на абиотический стресс // Экология. 1989. № 4. С. 20. Кабата-Пендиас А. Проблемы современной биохимии микроэлементов // Российский химический журнал (Ж. Рос. хим. общ-ва им Д.И.менделеева) 2005, т. XLIX, № 3, p. 15 Golovin A., Krinochkin L., Pevzner V. Geochemical specialization of bedrock and soil as indicator of regional geochemical endemicity./A. Golovin, L. Krinochkin, V. Pevzner // Geologija.- 2004.- Vol. 48.- P. 22-28. Хазиев Ф.Х. Методы почвенной энзимологии. Российская академия наук, Уфимский научный центр, Институт биологии. Москва, 2005. Быков Б.А. 'Экологический словарь' - Алма-Ата: 'Наука', 1983 – 216 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
