ок. Использование и анализ информационных моделей (таблицы, диаграммы, графики)
 Скачать 4.49 Mb. Скачать 4.49 Mb.
|
Ещё пример задания:Р-09. На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина кратчайшего пути из пункта А в пункт Ж не больше 15. Определите, какова длина кратчайшего пути из пункта Д в пункт В. В ответе запишите целое число – так, как оно указано в таблице. 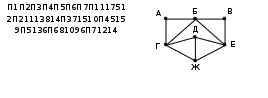 Решение: сложность этой задачи в том, что схема симметрична; легко понять, что без дополнительных данных (используя только степени вершин – количество связанных с ними ребёр) мы не сможем различить вершины А и В, Г и Е, Д и Ж определим степени вершин:
как и видно из рисунка, у нас две вершины степени 2 (А и В), две вершины степени 3 (Д и Ж) и три вершины степени 4 (Б, Г и Е), причем вершина Б однозначно определяется как вершина степени 4, которая связана с двумя вершинами степени 2 для того, чтобы различить оставшиеся вершины, определим длины путей ЖГА, ЖЕВ, ДГА и ДЕВ; мы не знаем, где какой маршрут, но точно знаем, что эти четыре маршрута П3 П1 П7 = 7 + 12 = 19 П3 П6 П5 = 10 + 6 = 16 П4 П1 П7 = 5 + 12 = 17 П4 П6 П5 = 9 + 6 = 15 из дополнительного условия (Известно, что длина кратчайшего пути из пункта А в пункт Ж не больше 15.) находим, что маршрут ЖГА – последний, так что П4 = Ж, П6 = Г и П5 = А; в итоге получается
кратчайший путь из Д в В можно найти с помощью дерева возможных маршрутов – это будет путь ДЕВ длиной 19 Ответ: 19. |
