ок. Использование и анализ информационных моделей (таблицы, диаграммы, графики)

• Название: Использование и анализ информационных моделей (таблицы, диаграммы, графики)
• Дата: 12.12.2022
• Размер: 4.49 Mb.
• Имя файла: ege1 (2).doc
• Тип: Документы; #840969
• страница: 8 из 16

Еще пример задания:

Р-01. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6». Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.

1)	2)	3)	4)
A B C D Е A 3 1 B 4 2 C 3 4 2 D 1 Е 2 2	A B C D Е A 3 1 1 B 4 C 3 4 2 D 1 Е 1 2	A B C D Е A 3 1 4 B 4 2 C 3 4 2 D 1 Е 4 2 2	A B C D Е A 1 B 4 1 C 4 4 2 D 1 4 Е 1 2

Решение (вариант 1):

1. 
   нужно рассматривать все маршруты из А в В, как напрямую, так и через другие станции
   
2. 
   рассмотрим таблицу 1:
   

• 
  из верхней строки таблицы следует, что из А в В напрямую везти нельзя, только через C (стоимость перевозки А-С равна 3) или через D (стоимость перевозки из А в D равна 1)
  

  	A	B	C	D	Е
  A			3	1

• 
  предположим, что мы повезли через C; тогда из третьей строки видим, что из C можно ехать в В, и стоимость равна 4
  

  	A	B	C	D	Е
  C	3	4			2

• 
  таким образом общая стоимость перевозки из А через С в В равна 3 + 4 = 7
  
• 
  кроме того, из С можно ехать не сразу в В, а сначала в Е:
  

	A	B	C	D	Е
C	3	4			2

а затем из Е – в В (стоимость также 2),

	A	B	C	D	Е
Е		2	2

так что общая стоимость этого маршрута равна 3  + 2 + 2 = 7

• 
  теперь предположим, что мы поехали из А в D (стоимость 1); из четвертой строки таблицы видим, что из D можно ехать только обратно в А, поэтому этим путем в В никак не попасть:
  

  	A	B	C	D	Е
  D	1

• 
  таким образом, для первой таблицы минимальная стоимость перевозки между А и В равна 7; заданное условие «не больше 6» не выполняется
  

3. 
   аналогично рассмотрим вторую схему; возможные маршруты из А в В:
   

• 
  , стоимость 7
  
• 
  , стоимость 7
  
• 
  таким образом, минимальная стоимость 7, условие не выполняется
  

4. 
   для третьей таблицы:
   

• 
  , стоимость 7
  
• 
  , стоимость 6
  
• 
  , стоимость 7
  
• 
  таким образом, минимальная стоимость 6, условие выполняется
  

5. 
   для четвертой:
   

• 
  , стоимость 9
  
• 
  , стоимость 8
  
• 
  минимальная стоимость 8, условие не выполняется
  

6. 
   условие «не больше 6» выполняется только для таблицы 3
   
7. 
   таким образом, правильный ответ – 3.
   

Возможные ловушки и проблемы: метод ненагляден, легко запутаться и пропустить решение с минимальной стоимостью

Решение (вариант 2, с рисованием схемы):

1. 
   для каждой таблицы нарисуем соответствующую ей схему дорог, обозначив стоимость перевозки рядом с линиями, соединяющими соседние станции:
   

1)	2)	3)	4)
A B C D Е A 3 1 B 4 2 C 3 4 2 D 1 Е 2 2	A B C D Е A 3 1 1 B 4 C 3 4 2 D 1 Е 1 2	A B C D Е A 3 1 4 B 4 2 C 3 4 2 D 1 Е 4 2 2	A B C D Е A 1 B 4 1 C 4 4 2 D 1 4 Е 1 2

2. 
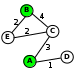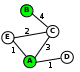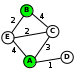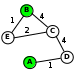   теперь по схемам определяем кратчайшие маршруты для каждой таблицы:
   

1: или , стоимость 7

2: или , стоимость 7

3: , стоимость 6

4: , стоимость 8

8. 
   условие «не больше 6» выполняется только для таблицы 3
   
9. 
   таким образом, правильный ответ – 3.
   

Возможные ловушки и проблемы: нужно внимательно строить схемы по таблицам, этот дополнительный переход (от табличных моделей к графическим) повышает наглядность, но добавляет еще одну возможность для ошибки наглядность схемы зависит от того, как удачно вы выберете расположение ее узлов; один из подходов – сначала расставить все узлы равномерно на окружности, нарисовать все связи и посмотреть, как можно расположить узлы более удобно по невнимательности можно пропустить решение с минимальной стоимостью