Курсовая работа ИСПОЛЬЗОВАНИЕ ЗАНИМАТЕЛЬНЫХ ЗАДАЧ ТЕОРИИ ГРАФОВ В ШКОЛЬНОМ КУРСЕ ИНФОРМАТИКИ. теоррия графов курсовая. Использование занимательных задач теории графов в школьном курсе информатики курсовая работа

• Название: Использование занимательных задач теории графов в школьном курсе информатики курсовая работа
• Анкор: Курсовая работа ИСПОЛЬЗОВАНИЕ ЗАНИМАТЕЛЬНЫХ ЗАДАЧ ТЕОРИИ ГРАФОВ В ШКОЛЬНОМ КУРСЕ ИНФОРМАТИКИ
• Дата: 07.04.2022
• Размер: 0.53 Mb.
• Имя файла: теоррия графов курсовая.docx
• Тип: Курсовая; #450739

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего образования

«Дальневосточный федеральный университет»

ШКОЛА ПЕДАГОГИКИ

Кафедра информатики, информационные технологии и методики обучения

Цыганок Анна Витальевна

ИСПОЛЬЗОВАНИЕ ЗАНИМАТЕЛЬНЫХ ЗАДАЧ ТЕОРИИ ГРАФОВ В ШКОЛЬНОМ КУРСЕ ИНФОРМАТИКИ

КУРСОВАЯ РАБОТА

	Студент гр. Б2405 _________________ (подпись)
	Руководитель ст. преп. Каф. ИИТМО _____________ И.А.Непочатых
Регистрационный № ________ ___________ ___________________ подпись И.О.Фамилия « _____» ___________________ 20 г.	Оценка _________________________ ____________ ___________________ подпись И.О.Фамилия «_____» ________________ 20 г.

г. Уссурийск

2019 г.

Оглавление

Введени

1.Теория графов в математике и информатике 6

1.1История возникновения теории графов 6

1.2Основные понятия теории графов 8

1.3Основные теоремы теории графов 10

1.4Способы предоставления графов в компьютере 12

1.4.1Требования к предоставлению графов 12

1.4.2Матрица смежности 13

1.4.3 Матрица инциденций 13

1.4.4Списки смежности 14

1.4.5Массив дуг 14

2.Применение теории графов при решении задач 16

2.1Обзор задач теории графов 16

2.2Общая характеристика задач 17

2.3Описание алгоритма решения задач 19

2.4Решение задач ОГЭ и ЕГЭ с использованием элементов теории графов 23

2.4.1Основные типы задач ОГЭ 23

2.4.2Основные типы задач ЕГЭ 28

1. Теория графов в математике и информатике 5

1.1 История возникновения теории графов 5

1.2 Основные понятия теории графов 7

1.3 Основные теоремы теории графов 9

1.4 Способы предоставления графов в компьютере 11

1.4.1 Требования к предоставлению графов 11

1.4.2 Матрица смежности 12

1.4.3 Матрица инциденций 12

1.4.4 Списки смежности 13

1.4.5 Массив дуг 13

2. Применение теории графов при решении задач 14

2.1 Обзор задач теории графов 14

2.2 Общая характеристика задач 15

2.3 Описание алгоритма решения задач 17

2.4 Решение задач ОГЭ и ЕГЭ с использованием элементов теории графов 21

2.4.1 Основные типы задач ОГЭ 21

2.4.2 Основные типы задач ЕГЭ 26

Заключение

Список использованных источников

Введение

Во многих случаях жизни нам приходиться рисовать на бумаге точки, изображающие населенные пункты, отдельные объекты, планировочные узлы и т.д.

Такие схемы под различными названиями встречаются всюду: магистральные и дорожные сети (в градостроительстве); электрические цепи, радиосхемы (в физике); диаграммы организации работ (в экономике); и т.д. В данной работе все эти схемы рассматриваются в абстрактной форме как самостоятельные математические объекты, названные графами.

Начало теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждении о Кенигсбергских мостах. Однако эта статья Эйлера (1736 г) была единственной в течение почти ста лет. Интерес к проблемам теории графов возродился около середины прошлого столетия. Имелось много причин для такого оживления изучения графов. Развитие формальной логики привело к изучению бинарных отношений в форме графов. Большое число популярных головоломок использовало формулировки в терминах графов. Наиболее знаменитая среди этих задач – проблема четырех, красок, впервые поставленная математиком Де Морганом в 1850 году.

В последние десятилетия отмечается неуклонное развитие теории графов. На этот процесс повлияли различные дисциплины: теория игр и программирования, теория передачи сообщений, теория электрических сетей и контактных цепей. Следствием этого явилось введение элементов графов в школу.

Графы являются простым и удобным языком для построения математических моделей различной степени сложности, эффективным средством для обучения школьников решению задач, связанных с анализом дискретных процессов. Изучение элементов теории графов играет значительную роль в формировании и развитии у учащихся потребности постоянно расширять и углублять свои знания, корректно формулировать и эффективно решать задачи в различных сферах практической деятельности.

Цель работы: изучение основ теории графов и ее применение в решении задач по информатике.

Задачи:

1. 
   Изучить учебную и методическую литературу по теме курсовой работы;
   
2. 
   рассмотреть основные положения теории графов, а также теоремы, лежащие в основе данной теории с доказательством;
   
3. 
   Рассмотреть ряд прикладных задач и их решение с применением теории графов.
   

Работа состоит из введения, двух глав, заключения и списка литературы. Во введении описывается актуализация темы, ставятся цели и задачи условия. В первой главе «Теория графов в математике и информатике» рассматривается такие вопросы как история возникновения теории графов, основные понятия и основные теоремы теории графов, а так же способы представления графов на компьютере. Во второй главе «Применение теории графов при решении задач» делается обзор задач теории графов, рассматриваются основные типы задач ОГЭ и ЕГЭ и их решение. В заключении делаются выводы о проделанной работе. Список литературы содержит 15 источников.

1. Теория графов в математике и информатике

1. История возникновения теории графов

Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.

Первые задачи теории графов были связаны с решением математических развлекательных задач и головоломок. Вот пересказ отрывка из письма Эйлера от 13 марта 1736 году: "Некогда мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство… После долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может. Кенигсбергские же мосты расположены так, что их можно представить на следующем рисунке (рис.1.1), на котором A обозначает остров, а B,C и D – части континента, отделенные друг от друга рукавами реки. Семь мостов обозначены буквами a, b, c, d, e, f, g" [4].

Обоснование вышеприведенного правила можно найти в письме Л. Эйлера к своему другу Элеру от 3 апреля того же года. Мы перескажем ниже отрывок из этого письма.

Математик писал, что переход возможен, если на участке разветвления реки имеется не более двух областей, в которые ведет нечетное число мостов. Для того, чтобы проще представить себе это, будем стирать на рисунке уже пройденные мосты. Легко проверить, что если мы начнем двигаться в соответствии с правилами Эйлера, пересечем один мост и сотрем его, то на рисунке будет изображен участок, где опять имеется не более двух областей, в которые ведет нечетное число мостов, а при наличии областей с нечетным числом мостов мы будем располагаться в одной из них. Продолжая двигаться так далее, пройдем через все мосты по одному разу.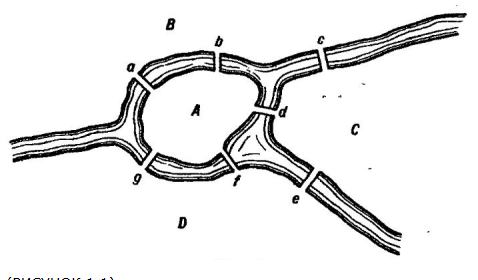



Рис.1.1

Правило Эйлера:

1. В графе, не имеющем вершин нечетных степеней, существует обход всех рёбер (причем каждое ребро проходится в точности один раз) с началом в любой вершине графа.

2. В графе, имеющем две и только две вершины с нечетными степенями, существует обход с началом в одной вершине с нечетной степенью и концом в другой.

3. В графе, имеющим более двух вершин с нечетной степенью, такого обхода не существует.

Существует еще один вид задач, связанных с путешествиями вдоль графов. Речь идёт о задачах, в которых требуется отыскать путь, проходящий через все вершины, причем не более одного раза через каждую. Цикл, проходящий через каждую вершину один и только один раз, носит название гамильтоновой линии (в честь Уильяма Роуэна Гамильтона, знаменитого ирландского математика прошлого века, который первым начал изучать такие линии). К сожалению, пока еще не найден общий критерий, с помощью которого можно было бы решить, является ли данный граф гамильтоновым, и если да, то найти на нём все гамильтоновы линии.

2. Основные понятия теории графов

Начнём с определения, однозначного определения теория графов не имеет, ниже представлены три определения, но существуют и другие.

Теория графов - раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами.

Теория графов - раздел математики, особенность которого - геометрический подход к изучению объектов

Теория графов - математический язык для формализованного определения понятий, связанных с анализом и синтезом структур систем и процессов.

Мы остановимся на следующем:

Теория графов - раздел математики исследующий свойства конечного множества элементов с заданными связями и отношениями между ними с помощью математических и графических средств.

Граф - Пара объектов G = ( X , Г ), где Х - конечное множество, а Г –конечное подмножество прямого произведения Х*Х. При этом Х называется множеством вершин , а Г - множеством дуг графа G [1].

Любое конечное множество точек (вершин), некоторые из которых попарно соединены стрелками, (в теории графов эти стрелки называются дугами), можно рассматривать как граф.

Если в множестве Г все пары упорядочены, то такой граф называют ориентированным.

Дуга - ребро ориентированного графа [5].

Граф называется вырожденным, если у него нет рёбер.

Вершина Х называется инцидентной ребру G , если ребро соединяет эту вершину с какой-либо другой вершиной.

Подграфом G(V1, E1) графа G(V, E) называется граф с множеством вершин V₁V и множеством ребер (дуг) E_ E, такими, что каждое ребро (дуга) из E1 инцидентно (инцидентна) только вершинам из V1. Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые рёбра (только те, оба конца которых входят в подграф) [1].

Вершины называются смежными, если существует ребро, их соединяющее.

Каждый граф можно представить в пространстве множеством точек, соответствующих вершинам, которые соединены линиями, соответствующими ребрам (или дугам - в последнем случае направление обычно указывается стрелочками). Такое представление называется укладкой графа.

Планарным называется граф, который может быть изображен на плоскости так, что его рёбра не будут пересекаться.

Пустым называется граф без рёбер. Полным называется граф, в котором каждые две вершины смежные.

Конечная последовательность необязательно различных рёбер E1,E2,...En называется маршрутом длины n, если существует последовательность V1, V2, ... Vn необязательно различных вершин, таких, что Ei = (Vi-1,Vi ).

Маршрут, в котором все рёбра попарно различны, называется цепью.

Замкнутый маршрут, все рёбра которого различны, называется циклом. Если все вершины цепи или цикла различны, то такая цепь или цикл называются простыми.

Маршрут, в котором все вершины попарно различны, называется простой цепью.

Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом [4].

Граф называется связным, если для любых двух вершин существует путь, соединяющий эти вершины.

Маршрут, содержащий все вершины или ребра графа и обладающий определенными свойствами, называется обходом графа.

Длина маршрута (цепи, простой цепи) равна количеству ребер а порядке их прохождения. Длина кратчайшей простой цепи, соединяющей вершины vi и vj в графе G, называется расстоянием d (vi, vj) между vi и vj [6].

Степень вершины - число ребер, которым инцидентна вершина V, обозначается D(V).

Петля - ребро оба конца которого принадлежат одной и той же вершине.

Два графа G1=(V1;E1), G2=(V2;E2),называются изоморфными, если существует взаимно-однозначное соответствие между множествами вершин V1 и V2 и между множествами рёбер Е1 и Е2, такое, чтобы сохранялось отношение инцидентности [6].

  Понятие изоморфизма для графов имеет наглядное толкование. Представим рёбра графов эластичными нитями, связывающими узлы – вершины. Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей.

3. Основные теоремы теории графов

Теорема 1. Удвоенная сумма степеней вершин любого графа равна числу его ребер [6].

Доказательство. Пусть  А₁, А₂, А₃, ..., A_n — вершины данного графа, a p(A₁), р(А₂), ..., p(A_n) – степени этих вершин. Подсчитаем число ребер, сходящихся в каждой вершине, и просуммируем эти числа. Это равносильно нахождению суммы степеней всех вершин. При таком подсчете каждое ребро будет учтено дважды (оно ведь всегда соединяет две вершины).

Отсюда следует: p(A₁)+р(А₂)+...+p(A_n)=0,5N, или 2(p(A₁)+р(А₂)+... +p(A_n))=N, где N — число ребер.

Теорема 2. Число нечетных вершин любого графа четно [4].

Доказательство. Пусть  a₁, a₂, a₃, …, a_k — это степени четных вершин графа, а  b₁, b₂, b₃, …, b_m — степени нечетных вершин графа. Сумма a₁+a₂+a₃+…+a_k+b₁+b₂+b₃+…+b_m ровно в два раза превышает число ребер графа. Сумма a₁+a₂+a₃+…+a_k четная (как сумма четных чисел), тогда сумма b₁+b₂+b₃+…+b_m должна быть четной. Это возможно лишь в том случае, если m — четное, то есть четным является и число нечетных вершин графа.

Эта теорема имеет следствия.

Следствие 1.Нечетное число знакомых в любой компании всегда четно.

Следствие 2.Число вершин многогранника, в которых сходится нечетное число ребер, четно.

Следствие 3. Число всех людей, когда-либо пожавших руку другим людям, нечетное число раз, является четным.

Теорема 3. Во всяком графе с n вершинами, где n больше или равно 2, всегда найдутся две или более вершины с одинаковыми степенями [2].

Доказательство. Если граф имеет n вершин, то каждая из них может иметь степень 0, 1, 2, ..., (n-1). Предположим, что в некотором графе все его вершины имеют различную степень, то есть, и покажем, что этого быть не может. Действительно, если р(А)=0, то это значит, что А — изолированная вершина, и поэтому в графе не найдется вершины Х со степенью р(Х)=n-1. В самом деле, эта вершина должна быть соединена с (n-1) вершиной, в том числе и с А, но ведь А оказалась изолированной. Следовательно, в графе, имеющем n вершин, не могут быть одновременно вершины степени 0 и (n-1). Это значит, что из n вершин найдутся две, имеющие одинаковые степени.

Теорема 4. Если в графе с n вершинами (n больше или равно 2) только одна пара имеет одинаковую степень, то в этом графе всегда найдется либо единственная изолированная вершина, либо единственная вершина, соединенная со всеми другими.

Доказательство данной теоремы мы опускаем. Остановимся лишь на некотором ее пояснении. Содержание этой теоремы хорошо разъясняется задачей: группа, состоящая из n школьников, обменивается фотографиями. В некоторый момент времени выясняется, что двое совершили одинаковое число обменов. Доказать, что среди школьников есть либо один еще не начинавший обмена, либо один уже завершивший его.

Теорема 5. Если у графа все простые циклы четной длины, то он не содержит ни одного цикла четной длины [2].

Теорема 6. Для того, чтобы граф был эйлеровым, необходимо и достаточно, чтобы он был связным и все его вершины имели четную степень.

Теорема 7. Для того чтобы на связном графе можно было бы проложить цепь АВ, содержащую все его ребра в точности по одному разу, необходимо и достаточно, чтобы А и В были единственными нечетными вершинами этого графа.

Теорема 8. Если данный граф является связным и имеет 2k вершин нечетной степени, то в нем можно провести k различных цепей, содержащих все его ребра в совокупности ровно по одному разу [5].

4. Способы предоставления графов в компьютере

Конструирование структур данных для представления в программе объектов математической модели – это основа искусства практического программирования. Далее приводится четыре различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных представлений, общее число которых необозримо. Но все они так или иначе основаны на тех базовых идеях, которые описаны в этом разделе.

1. Требования к предоставлению графов

Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены четыре наиболее часто используемых представления с указанием характеристики n(p,q) – объема памяти для каждого представления. Здесь p – число вершин, а q – число ребер.

2. Матрица смежности

Представление графа с помощью квадратной булевой матрицы M, отражающей смежность вершин, называется матрицей смежности, где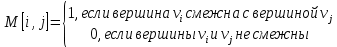



Для матрицы смежности n(p,q) = O(p²).

Замечание

Матрица смежности неориентированного графа симметрична относительно главной диагонали, поэтому достаточно хранить только верхнюю (или нижнюю) треугольную матрицу.

3. Матрица инциденций

Представление графа с помощью матрицы H, отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа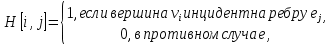



а для орграфа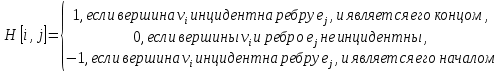



Для матрицы инциденций n(p,q) = O(pq) [3].

4. Списки смежности

Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей на списки смежных вершин, где элемент списка представлен структурой

N : record v : 1..p; n :↑ N end record,

называется списком смежности. В случае представления неориентированных графов списками смежности n(p,q) = O(p+2q), а в случае ориентированных графов n(p,q) = O(p+q).

5. Массив дуг

Представление графа с помощью массива структур

E : array [1..q] of record b,e : 1..p end record,

отражающего список пар смежных вершин, называется массивом ребер (или, для орграфов, массивом дуг). Для массива ребер (или дуг) n(p,q) = O(2q) [3].

В данной в данной главе была рассмотрена история возникновения теории графов. Основными понятиями теории графов являются такие понятия как граф, подграф, цикл, цепь. Было выяснено, что смежными являются графы, в которых существует ребро, соединяющее вершины, а изоморфными – графы, в которых все вершины смежны. Рассмотрены теоремы для графов с n вершинами, для смежных графов, а так же для графов с циклами. Рассмотрены такие способы представления графов на компьютере, как матрица смежности, матрица инциденций, списки смежности и массив дуг.

2. Применение теории графов при решении задач

1. Обзор задач теории графов

Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из всех математических объектов графы занимают одно из первых мест в качестве формальных моделей реальных систем.

Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.

Далее перечислим некоторые типовые задачи теории графов и их приложения:

- Задача о кратчайшей цепи

замена оборудования

составление расписания движения транспортных средств

размещение пунктов скорой помощи

размещение телефонных станций

- Задача о максимальном потоке

анализ пропускной способности коммуникационной сети

организация движения в динамической сети

оптимальный подбор интенсивностей выполнения работ

задача о распределении работ

- Задача об упаковках и покрытиях

оптимизация структуры ПЗУ

размещение диспетчерских пунктов городской транспортной сети

- Раскраска в графах

распределение памяти в ЭВМ

проектирование сетей телевизионного вещания

- Связность графов и сетей

проектирование кратчайшей коммуникационной сети

синтез структурно-надежной сети циркуляционной связи

анализ надежности стохастических сетей связи

- Изоморфизм графов и сетей

структурный синтез линейных избирательных цепей

автоматизация контроля при проектировании БИС

- Изоморфное вхождение и пересечение графов

локализация неисправности с помощью алгоритмов поиска МИПГ

покрытие схемы заданным набором типовых подсхем

- Автоморфизм графов

конструктивное перечисление структурных изомеров для производных органических соединений

синтез тестов цифровых устройств

2. Общая характеристика задач

В данном разделе будут рассмотрены различные задачи, которые можно использовать на уроках в школьном курсе информатики, а так же способы их решения.

Задача 1. Между планетами введено космическое сообщение по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса?

Задача 2. В обеденный перерыв члены строительной бригады разговорились о том, кто сколько газет читает. Выяснилось, что каждый выписывает и читает две и только две газеты, каждую газету читает пять человек, и любая комбинация газет читается одним человеком. Сколько различных газет выписывают члены бригады? Сколько человек в бригаде? [10]

Задача 3. Необходимо составить фрагмент расписания для одного дня с учетом следующих обстоятельств:

• 
  учитель истории может дать либо первый, либо второй, либо третий уроки, но только один урок;
  
• 
  учитель литературы может дать один, либо второй, либо третий урок;
  
• 
  математик готов дать либо только первый, либо только второй урок;
  
• 
  преподаватель физкультуры согласен дать только последний урок.
  

Сколько и каких вариантов расписания, удовлетворяющего всем вышеперечисленным условиям одновременно, может составить завуч школы? [10].

Задача 4. Для составления цепочек используются бусины, помеченные буквами: A, B, C, D, E. На первом месте в цепочке может стоять одна из бусин A, C, D. На втором – любая бусина с согласной буквой, если первая бусина – с гласной буквой, и любая бусина с гласной, если первая - с согласной. На третьем месте находится одна из бусин с буквами C, D, E, не стоящей в цепочке на первом или втором месте. Сколько цепочек можно создать по этому правилу? Для решения задачи постройте и проанализируйте дерево [7].

Задача 5. Марина, Лариса, Жанна и Катя умеют играть на разных инструментах (пианино, виолончели, гитаре, скрипке), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и испанский), но каждая только один. Известно:

1. Девушка, которая играет на гитаре, говорит по-испански.

2. Лариса не играет ни на скрипке, ни на виолончели и не знает английского языка.

3. Марина не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского.

4. Девушка, которая говорит по-немецки, не играет на виолончели.

5. Жанна знает французский язык, но не играет на скрипке.

Определить, кто на каком инструменте играет, и какой иностранный язык знает [7].

Задача 6. На рисунке дан план подземелья, в одной из комнат которого скрыт ключ нужный вам. Для отыскания ключа достаточно войти в одну из крайних комнат подземелья, пройти через все двери, причем в точности по одному разу через каждую. Ключ скрыт за той дверью, которая будет пройдена последней. Укажите номер комнаты, в которой спрятан ключ [8].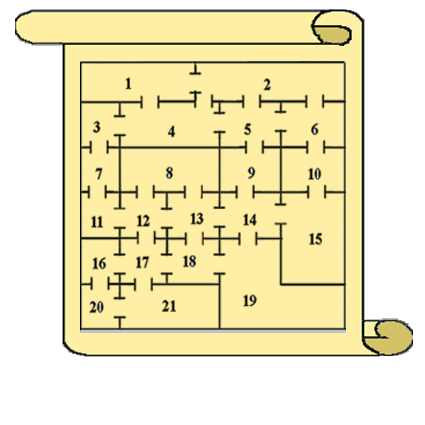



Рис. 2.1

3. Описание алгоритма решения задач

Опишем решение каждой задачи.

Решение задачи 1.

Нарисуем схему: планетам будут соответствовать точки, а соединяющим их маршруты – не пересекающиеся между собой линии.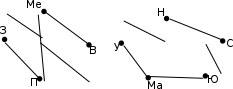



Рис. 2.2

Из данного графа сразу становится видно что маршрута с Земли до Марса не имеется.

Решение задачи 2.

Построим граф, в котором каждая вершина обозначает соответствующую газету, а каждое ребро будет соответствовать одному подписчику.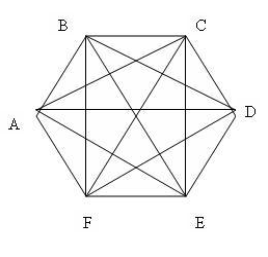



Рис. 2.3

Граф полный. Степень каждой вершины равна 5, вершин 5+1=6, число ребер 6*5/2=15. Значит, число газет 6, человек в бригаде 15.

Решение задачи 3.

Эту задачу можно решить путем обыкновенного перебора всех возможных вариантов, но решение будет наиболее простым, если вычертить граф в виде дерева.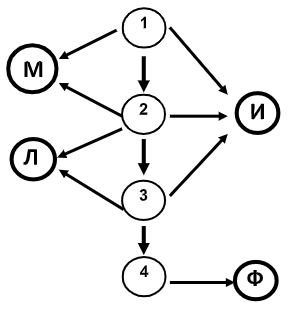



Рис. 2.4

Построим деревья всех возможных вариантов.



Рис. 2.5



Рис. 2.6

Таким образом, получаем 3 варианта: ИМЛФ, МИЛФ, МЛИФ.

Решение задачи 4.

Для решения задачи составим дерево со всеми вариантами.



Рис. 2.7

Посчитаем количество получившихся вариантов и получим ответ 13.

Решение задачи 5.



Рис. 2.8

Из пятого условия, что Жанна знает французский язык, рисуем стрелку. Из третьего условия, что Марина не знает ни немецкого, ни английского, а французский знает Жанна, то Марина знает испанский и, рассматривая первое условие она играет на гитаре. Из условия 2 видим, что Лариса играет на пианино, т.к. Марина играет на гитаре, а на других инструментах она играть не умеет, и значит, она говорит по-немецки.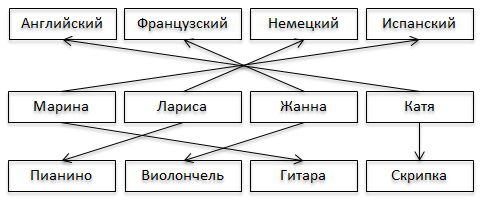



Рис.2.9

Т.к. Жанна не играет на скрипке, то остается один инструмент, на котором она может играть это виолончель. Тогда Катя играет на скрипке, и знает английский язык.

Решение задачи 6.

Составим граф, соответствующий подземелью, в котором вершины – комнаты, а ребра соединяют те вершины, которые соответствуют комнатам, связанным дверью.



Рис. 2.10

Данный граф имеет эйлеров путь, так как только две вершины имеют нечётную степень, это вершины 6 и 18. Значит, вход и выход могут быть только в вершинах 6 и 18.

Так как комната 6 является крайней, то в ней будет вход, значит, последней комнатой будет 18-ая, следовательно сокровища скрыты в этой комнате.

4. Решение задач ОГЭ и ЕГЭ с использованием элементов теории графов

1. Основные типы задач ОГЭ

Один из видов задач, которые рассматриваются в ОГЭ, это задачи на нахождение кратчайшего пути. Они представлены под номером 3 (Формальные описания реальных объектов и процессов).

Задача 1.

Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых (в километрах) приведена в таблице:



Рис. 2.11

Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

1) 9

2) 11

3) 13

4) 15

Рассмотрим подробное решение данной задачи.

1. 
   Построим граф, соответствующий таблице.
   

Построение графа начнем с размещения узлов (населенных пунктов), располагая их «по кругу», а затем последовательно изобразим все указанные в таблице дороги. Так же на ребрах укажем длины данных дорог.



Рис. 2.12

2. 
   Анализ графа.
   

Для того чтобы найти оптимальный маршрут из A в E перечислим все возможные маршруты из А в F:

A—F: длина марш­ру­та 15 км.

A—B—C—E—F: длина марш­ру­та 15 км.

A—B—C—D—F: длина марш­ру­та 14 км.

A—C—E—F: длина марш­ру­та 14 км.

A—C—D—F: длина марш­ру­та 13 км.

Таким образом определяем что длина минимального маршрута состовляет 13 км.

Правильный ответ указан под номером 3.

Еще один распространенный тип задач, рассматриваемый в ОГЭ это задачи на поиск количества путей, представленный под номером 11 (Анализирование информации, представленной в виде схем).

Задача 2.

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К [12]?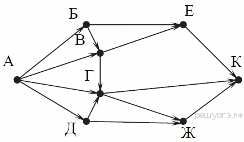


Рис. 2.13

Главную идею решения: (число дорог в город N есть сумма дорог, приводящих в города, из которых есть прямой проезд в город N), отразим на самой схеме, показывая на ней ЧИСЛО ДОРОГ, приводящих в каждый город.

Последовательность очевидна: начинаем с Б и Д (городов, куда есть по 1-й дороге из А)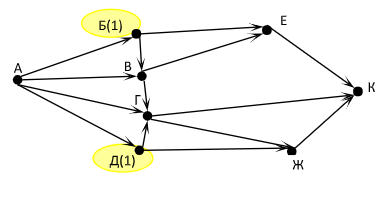


Рис. 2.14

Посчитаем дороги в В: 1 (из A)+ 1(дороги города Б)= 2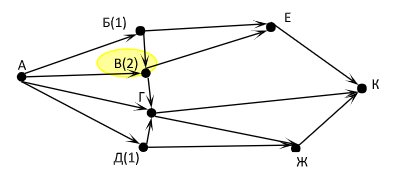



Рис.2.15

В город Г входят уже 3 дороги: 1 (из A)+ 2(дороги города В)+ 1(дороги города Д)= 4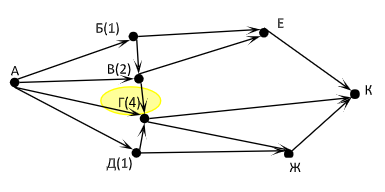



Рис. 2.16

Аналогично посчитаем дороги в Е и Ж: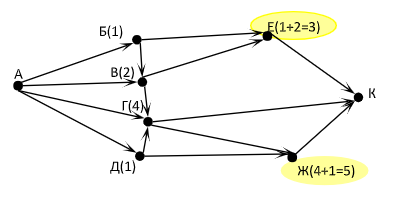



Рис. 2.17

Определяем число дорог в город К, как сумму дорог в города, с которыми он связан: Г, Ж, Е.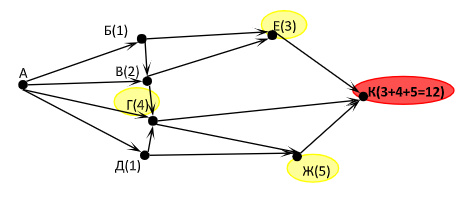



Рис. 2.18

Таким образом, правильный ответ 12.

2. Основные типы задач ЕГЭ

В ЕГЭ, как и в ОГЭ, имеются задачи на нахождение кратчайшего пути и нахождение количества путей, только более усложненные. Их рассматривать не будем.

С помощью графов можно решать задачи на поиск алгоритма минимальной длины для исполнителя.

Задача 1.

У исполнителя Утроитель две команды, которым присвоены номера

1. Прибавь 1;

2. Умножь на 3.

Запишите порядок команд в программе преобразования числа 1 в число 22, содержащей не более 5 команд [11]

Для решения данного задания используем метод от обратного, то есть будем преобразовывать число 22 в 1. Соответственно команды исполнителя заменим командами обратными, то есть команду «Прибавь 1» заменим командой «Вычти 1», а «Умножь на 3» заменим командой «Раздели на 3». Ход выполнения команд можно изобразить в виде дерева, каждая вершина которого имеет две ветки, соответствующие командам 1 и 2. Корнем этого дерева является число 22. Это дерево будет иметь 5 ярусов, так как программа должна содержать не более 5 команд. Но здесь нужно учесть один момент. Если число делится на 3, то вершина будет иметь 2 ветви, а если нет, то одну (то есть делить на 3 мы не можем, а можем только вычитать 1). Получаем следующее дерево.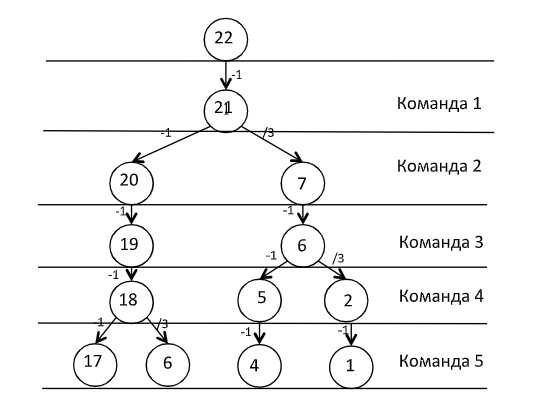



Рис. 2.19

Учитывая номера команд, записываем программу решения данной задачи в виде последовательности соответствующих команд.

Таким образом наш ответ 12121.

Так же с помощью графов можно решать некоторые задачи на кодирование информации.

Задача 2.

Для кодирования некоторой последовательности, состоящей из букв А, Б, В и Г, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Для букв А, Б, В используются такие кодовые слова: А — 000, Б — 1, В — 011.

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением [14]

Для решения данной задачи построим дерево для заданного двоичного кода: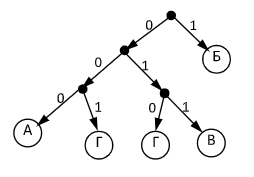


Рис. 2.20

согласно условию Фано, код декодируется однозначно, если все используемые кодовые слова соответствуют листьям такого дерева; видим, что для заданных кодовых слов это условие выполняется

Из данного дерева видно, что букву Г можно «подвесить» либо на ветвь 001, либо на ветвь 010. В условии сказано что нужно выбрать наименьший код поэтому наш ответ будет 001.

Все задания под номером 26, которые направлены на поиск выигрышной стратегии, нужно решать с помощью графов. Рассмотрим одну их них.

Задача 3.

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или пять камней или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 20 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 42.

Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 42 или больше камней. В начальный момент в куче было S камней; 1 ≤ S ≤ 41.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может

встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

Задание 1.

а) Укажите все такие значения числа S, при которых Петя может выиграть

в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающие ходы.

б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

Задание 2.

Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:

- Петя не может выиграть за один ход;

- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Для каждого указанного значения S опишите выигрышную стратегию Пети.

Задание 3.

Укажите значение S, при котором одновременно выполняются два условия:

- у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

- у Вани нет стратегии, которая позволит ему гарантированно выиграть

первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани.

Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах — количество камней в позиции. [15]
Решим задачи поочередно.

Задание 1.

а) Петя может выиграть, если S = 14, …, 41. Чтобы получить кучу, содержащую не менее 40 камней, достаточно утроить исходное количество камней. При меньших значениях S за один ход нельзя получить кучу, в которой не менее 42 камней.

б) Ваня может выиграть первым ходом (как бы ни играл Петя), если исходно в куче будет S = 13 камней. Тогда после первого хода Пети в куче будет 14, 18 или 39 камней. Во всех случаях Ваня утраивает количество камней и выигрывает в один ход.

 Задание 2.

Возможные значения S: 8, 12. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 13 камней. Эта позиция разобрана в п. 1 б. В ней игрок, который будет ходить (теперь это Ваня), выиграть не может, а его противник (то есть Петя) следующим ходом выиграет.

 Задание 3.

Возможные значения S: 7, 11.

Например, для S = 7 после первого хода Пети в куче будет 8 камней, 12 камней или 21 камень. Если в куче станет 21 камень, Ваня утроит количество камней и выиграет первым ходом. Ситуация, когда в куче 8 или 12 камней, разобрана в п. 2. В этой ситуации игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.

 В рисунке изображено дерево возможных партий при описанной стратегии Вани для первого возможного значения. При выбранной стратегии на последнем ходе Ваня утраивает количество камней. Заключительные позиции (в них выигрывает Ваня) выделены.



Рис. 2.21

Во второй главе были рассмотрены такие задачи как нахождение путей между городами, поиск выхода из лабиринта, перебор всех возможных вариантов составления расписания. Некоторые задачи были решены задачи с помощью построения дерева. Были рассмотрены задачи ОГЭ на поиск кратчайшего пути и поиск количества путей между городами. Были рассмотрены задачи ЕГЭ на поиск алгоритма минимальной длины для исполнителя, на кодирование информации, а так же задача на поиск выигрышной стратегии.
Заключение

В данной работе были рассмотрены основные понятия теории графов, их виды. Рассмотрели ряд теорем и свойств. Описали способы представления графов, а в практической части показали их применение на конкретных задачах.

Известно, что графы получили широкое распространение и популярность благодаря тому, что многие головоломки и задачи можно решить с использованием знаний теории графов. Частные примеры таких головоломок и сюжетных задач были приведены в практической части. Так же были рассмотрены различные виды задач из ОГЭ и ЕГЭ. Задачи на отыскание путей через лабиринты, близкие к задачам на эйлеровы графы, находят применение в современной психологии и при конструировании вычислительных машин. Также с практической точки зрения, сейчас графы применяют во многих других областях науки таких как: программирование, физика, химия, биология, экономика и т.д.
Список использованных источников

1. 
   Андерсон, Джеймс А. Дискретная математика и комбинаторика: пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 960с.
   
2. 
   Березина, Л. Ю. Графы и их применение. – М.: Просвещение, 1979. – 814с.
   
3. 
   Демоверсия ЕГЭ по информатике. [Электронный ресурс] – Режим доступа: https://4ege.ru/informatika/56937-demoversiya-ege-2019-po-informatike.html Дата посещения – 14.01.2018
   
4. 
   Зыков, А. А. Основы теории графов. — М.: Вузовская книга, 2004. — 664с.
   
5. 
   Касаткин, В. Н. Необычные задачи математики, Киев, «Радяньска школа» 1987
   
6. 
   Мельников, О.И. Теория графов в занимательных задачах. - М.: Книжный дом «ЛИБРОКОМ», 2009. - 232 с.
   
7. 
   Новиков, С.А. Дискретная математика для программистов – СПб.: Питер, 2001. – 304с.
   
8. 
   Олехник С.Н, Нестеренко Ю.В., Потапов М.К. Старинные занимательные задачи, М.: Наука, 1988
   
9. 
   Оре, O. Графы и их применение. – М.: Мир,1973. – 175с.
   
10. 
    Поляков, К.Ю. ЕГЭ по информатике (2019). [Электронный ресурс] – Режим доступа: http://kpolyakov.spb.ru/school/ege.htm Дата посещения – 12.01.2018
    
11. 
    РЕШУ ЕГЭ: информатика. [Электронный ресурс] – Режим доступа: https://inf-ege.sdamgia.ru Дата посещения – 13.01.2018
    
12. 
    Уилсон, Р. Введение в теорию графов. – М.: Мир, 1977. – 210с.
    
13. 
    Ушаков, Д.М. Информатика: большой сборник тематических заданий по информатике для подготовки к ОГЭ. — М.: изд. АСТ, 2018. – 203с. [Электронный ресурс] – Режим доступа: https://drive.google.com/file/d/1RcAQl8EbJQ7UCjcMG4zwo0SzQhp-1185/view Дата посещения – 14.01.2018
    
14. 
    Ушаков, Д.М. Информатика: большой сборник тематических заданий по информатике для подготовки к ЕГЭ. — М.: изд. АСТ, 2018. – 312с. [Электронный ресурс] – Режим доступа: https://drive.google.com/file/d/1iydLXfI49EXpXAXbp7YArgWh8Zgx1NUW/view Дата посещения – 14.01.2018
    
15. 
    Харари, Ф. Теория графов. – М.: Мир, 1973. – 301с.