Главная страница
Навигация по странице:

  • Функция {\displaystyle F_{k}}

  • Предобработка

  • Итеративная обработка

  • Постобработка

    		•

    Исследование алгоритмов современных зарубежных симметричного шифров feal


    Скачать 160.86 Kb.
    НазваниеИсследование алгоритмов современных зарубежных симметричного шифров feal
    Дата10.04.2023
    Размер160.86 Kb.
    Формат файлаdocx
    Имя файлаPZ-2-FEAL-theory-OLGIN-I-A.docx
    ТипИсследование
    #1049546

    06.02


    Ольгин И.А. 3ОИБАС-1020

    ПЗ-2, часть 1. Исследование алгоритмов современных зарубежных симметричного шифров: FEAL

    Теоретические сведения

    Опубликованный в 1987 году Акихиро Симидзу и Сёдзи Миягути блочный шифр FEAL был разработан с целью повысить скорость шифрования без ухудшения надежности шифра, по сравнению с DES. Первоначально алгоритм использовал блоки размером 64 бита, ключ размером 64 бита и 4 раунда шифрования. Однако, уже в 1988 году была опубликована работа Берта ден Боера (англ. Bert Den-Boer) , доказывающая достаточность владения 10000 шифротекстов для проведения успешной атаки на основе подобранного открытого текста. К шифру FEAL одному из первых был применен линейный криптоанализ. В том числе в 1992 году Митсуру Мацуи и Ацухиро Ямагиси доказали, что достаточно узнать 5 шифротекстов для проведения успешной атаки.

    Для борьбы с обнаруженными уязвимостями создатели удвоили число раундов шифрования, опубликовав стандарт FEAL-8. Однако, уже в 1990 году Генри Гилберт (англ. Henri Gilbert) обнаружил уязвимость и этого шифра перед атакой на основе подобранного открытого текста. Далее в 1992 году Мицуру Мацуи и Ацухиро Ямагиси (Mitsuru Matsui and Atsuhiro Yamagishi) описали атаку на основе открытых текстов, требующую   известных шифротекстов[3].

    В связи с большим числом успешных атак, разработчиками было принято решение еще усложнить шифр. А именно, в 1990 году был представлен FEAL-N, где N — произвольное четное число раундов шифрования, и представлен FEAL-NX, где X (от англ. extended) обозначает использование расширенного до 128 бит ключа шифрования. Однако данное нововведение помогло лишь частично. В 1991 году Эли Бихам и Ади Шамир, используя методы дифференциального криптоанализа, показали возможность взлома шифра с числом раундов   быстрее, чем полным перебором.

    Тем не менее, благодаря интенсивности исследования алгоритма шифрования сообществом, были доказаны границы уязвимости шифра перед линейным и дифференциальным криптоанализом. Устойчивость алгоритма с числом раундов большим 26 к линейному криптоанализу показали в своей работе Сихо Мораи, Кадзумаро Аоки и Кадзуо Ота, а в работе Казумаро Аоки, Кунио Кобаяси и Шихо Мораи была доказана невозможность применить дифференциальный криптоанализ к алгоритму, использующему больше 32 раундов шифрования.

    В качестве входа процесса шифрования в алгоритме FEAL-NX используется 64-битовый блок открытого текста. Процесс шифрования разбит на 3 стадии.

    1. Предобработка

    2. Итеративное вычисление

    3. Постобработка

    Кроме того, описан процесс генерации раундовых ключей, с которого и начинается шифрование, а также функции  , с помощью которых и производятся преобразования.

    Определим (A,B) — операцию конкатенации двух последовательностей бит.

    Определим   — нулевой блок длины 32 бита.

    Функция S

    {\displaystyle S_{0}(a,b)}  = циклический сдвиг влево на 2 бита {\displaystyle ((a+b)\mod {256})}

    {\displaystyle S_{1}(a,b)}  = циклический сдвиг влево на 2 бита {\displaystyle ((a+b+1)\mod {256})}

    Функция F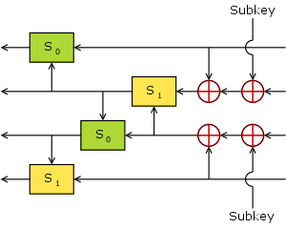



    Рис. Схема функции F

    Функция F берёт 32 бита данных и 16 битов ключа и смешивает их вместе.

    Функция F берёт 32 бита данных и 16 битов ключа и смешивает их вместе.

    1. {\displaystyle F=F(\alpha ,\beta )=(F_{0},F_{1},F_{2},F_{3})}

    2. {\displaystyle \alpha =(\alpha _{0},\alpha _{1},\alpha _{2},\alpha _{3});\;\beta =(\beta _{0},\beta _{1})}

    3. {\displaystyle F_{1}=\alpha _{1}\oplus \beta _{0}}

    4. {\displaystyle F_{2}=\alpha _{2}\oplus \beta _{1}}

    5. {\displaystyle F_{1}=F_{1}\oplus \alpha _{0}}

    6. {\displaystyle F_{2}=F_{2}\oplus \alpha _{3}}

    7. {\displaystyle F_{1}=S_{1}(F_{1},F_{2})}

    8. {\displaystyle F_{2}=S_{0}(F_{2},F_{1})}

    9. {\displaystyle F_{0}=S_{0}(\alpha _{0},F_{1})}

    10. {\displaystyle F_{3}=S_{1}(\alpha _{3},F_{2})}

    Функция {\displaystyle F_{k}}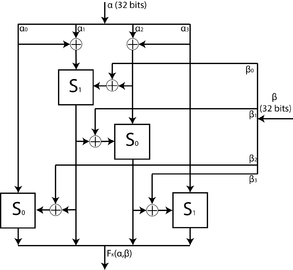



    Рис. Схема функции 
    Функция   работает с двумя 32 битовыми словами.

    Функция {\displaystyle F_{k}}  работает с двумя 32 битовыми словами.

    1. {\displaystyle F_{k}=F_{k}(\alpha ,\beta )=(F_{k_{0}},F_{k_{1}},F_{k_{2}},F_{k_{3}})}

    2. {\displaystyle \alpha =(\alpha _{0},\alpha _{1},\alpha _{2},\alpha _{3});\;\beta =(\beta _{0},\beta _{1},\beta _{2},\beta _{3})}

    3. {\displaystyle F_{k_{1}}=\alpha _{1}\oplus \alpha _{0}}

    4. {\displaystyle F_{k_{2}}=\alpha _{2}\oplus \alpha _{3}}

    5. {\displaystyle F_{k_{1}}=S_{1}(F_{k_{1}},(F_{k_{2}}\oplus \beta _{0}))}

    6. {\displaystyle F_{k_{2}}=S_{0}(F_{k_{2}},(F_{k_{1}}\oplus \beta _{1}))}

    7. {\displaystyle F_{k_{0}}=S_{0}(\alpha _{0},(F_{k_{1}}\oplus \beta _{2}))}

    8. {\displaystyle F_{k_{3}}=S_{1}(\alpha _{3},(F_{k_{2}}\oplus \beta _{3}))}

    Генерация раундовых ключей



    Рис. Схема генерации раундовых ключей

    В результате генерации раундовых ключей, из полученного на вход ключа длиной 128 бит получается набор из N+8 раундовых ключей {\displaystyle K_{i}} , длиной 16 бит каждый. Данный результат получается в результате следующего алгоритма.

    1. Разделение входного ключа на левый и правый ключ: {\displaystyle K=(K_{L},K_{R})} , они имеют длину 64 бита.

    2. Обработка ключа {\displaystyle K_{R}=(K_{R1},K_{R2})}

    3. Введение временной переменной {\displaystyle Q_{r}}  для {\displaystyle 1\leq r\leq {\frac {N}{2}}+4} :

      • {\displaystyle Q_{r}=K_{R1}\oplus K_{R2},\;r=3i-2,\;i\in \mathbb {N} }

      • {\displaystyle Q_{r}=K_{R1},\;r=3i-1,\;i\in \mathbb {N} }

      • {\displaystyle Q_{r}=K_{R2},\;r=3i,\;i\in \mathbb {N} }

    4. Обработка ключа {\displaystyle K_{L}=(A_{0},B_{0})}

    5. Введение временной переменной {\displaystyle D_{0}=\phi }

    6. Последовательное вычисление {\displaystyle K_{i}}

      • {\displaystyle D_{r}=A_{r-1}}

      • {\displaystyle A_{r}=B_{r-1}}

      • {\displaystyle B_{r}=F_{k}(A_{r-1},(B_{r-q}\oplus D_{r-1})\oplus Q_{r}))=(B_{r_{0}},B_{r_{1}},B_{r_{2}},B_{r_{3}})}

      • {\displaystyle K_{2(r-1)}=(B_{r_{0}},B_{r_{1}})}

      • {\displaystyle K_{2(r-1)+1}=(B_{r_{2}},B_{r_{3}})}

    Предобработка

    На начальной стадии блок данных {\displaystyle P}  готовится к итеративной процедуре шифрования.

    1. {\displaystyle P=(L_{0},R_{0})}

    2. {\displaystyle (L_{0},R_{0})=(L_{0},R_{0})\oplus (K_{N},K_{N+1},K_{N+2},K_{N+3})}

    3. {\displaystyle (L_{0},R_{0})=(L_{0},R_{0})\oplus (\phi ,L_{0})}

    Итеративная обработка

    На этой стадии с блоком данных производится N раундов перемешивания битов по следующему алгоритму.

    1. {\displaystyle R_{r}=L_{r-1}\oplus F(R_{r-1},K_{r-1})}

    2. {\displaystyle L_{r}=R_{r-1}}

    Постобработка

    Задача этой стадии — подготовить почти готовый шифротекст к выдаче.

    1. {\displaystyle P=(R_{N},L_{N})}

    2. {\displaystyle P=P\oplus (\phi ,R_{N})}

    3. {\displaystyle P=P\oplus (K_{N+4},K_{N+5},K_{N+6},K_{N+7})}

    Тот же алгоритм может быть использован для дешифрования. Единственным отличием является то, что при дешифровании порядок использования частей ключа меняется на обратный.

    Хотя изначально алгоритм FEAL задумывался, как более быстродействующая замена DES, в том числе, для применения шифрования в смарт-картах, количество быстро найденных в нем уязвимостей поставило точку на перспективах использования данного алгоритма. К примеру, в работе Эли Бихама и Ади Шамира, опубликованной в 1991 году, доказана достаточность 8 выбранных открытых текстов для взлома шифра FEAL-4, 2000 — для взлома FEAL-8, {\displaystyle 2^{28}}  — для FEAL-16. Все эти числа значительно меньше необходимого числа выбранных открытых текстов для атаки на DES, а тот факт, что FEAL-32 достаточно надежен, достаточно бесполезен, так как DES добивается сравнимой надежности при значительно меньшем числе раундов, тем самым лишая FEAL преимущества, изначально задумывавшегося создателями.

    На данный момент на официальном сайте авторов шифра — компании NTT, в описании шифра FEAL вывешено предупреждение, о том что компания NTT рекомендует не использовать шифр FEAL, а использовать шифр Camelia, также разработанный этой компанией ради надежности и скорости шифрования.

    Благодаря тому, что шифр FEAL был разработан достаточно рано, он послужил отличным объектом для тренировок для криптологов всего мира[10].

    Кроме того, на его примере был открыт линейный криптоанализ. Мицуру Мацуи, изобретатель линейного криптоанализа, в первой своей работе на эту тему рассматривал как раз FEAL и DES.

    написать администратору сайта