Основы теории цепей. ОТЦ_530. Исследование частотных и переходных характеристик активных rcцепей Курсовая работа по курсу "Основы теории цепей"
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
К  АЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А. Н. ТУПОЛЕВА Радиотехнический факультет Кафедра теоретической радиотехники и электроники Исследование частотных и переходных характеристик активных RC-цепей Курсовая работа по курсу "Основы теории цепей" Выполнил студент Принял преподаватель КАЗАНЬ 2004 г. Содержание № стр. 1. Вывод передаточных характеристик 4 2. Построение карты особых точек 6 3. Расчет и построение частотных характеристик 8 Расчет и построение переходных характеристик 12 Выводы. 15 Список литературы 15 1. Вывод передаточных характеристик Ku(p) и Z11(p). Для вывода коэффициента передачи по напряжению и входного сопротивления необходимо составить систему уравнений в матричной форме на базе метода узловых потенциалов. Для этого зададим на входе схемы источник энергии в виде идеального источника тока I0. Схема фильтра приведена на рис. 1.1. 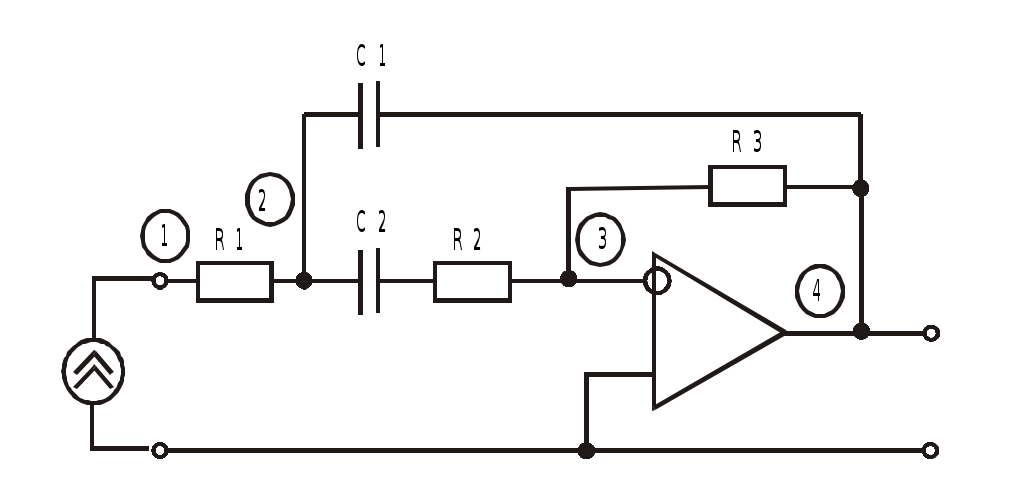 Рис. 1.1. Схема ARC-цепи. Преобразуем схему с учетом схемы замещения операционного усилителя (рис. 1.2.) и пронумеруем узлы схемы. 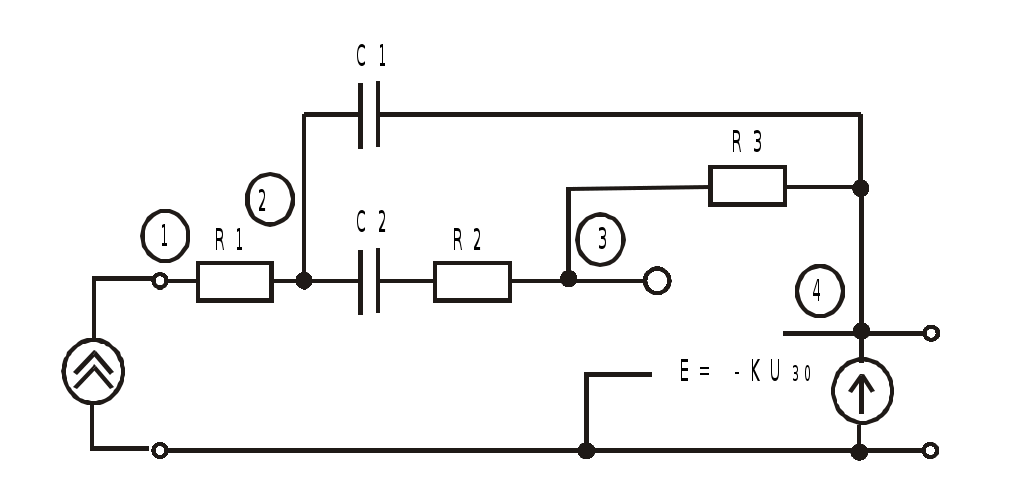 Рис. 1.2. Схема замещения. При составление системы уравнений по методу узловых потенциалов следует учесть, что к четвертому узлу подключен источник ЭДС, поэтому для этого узла уравнение не составляем. Система уравнений в матричной форме выглядит следующим образом: 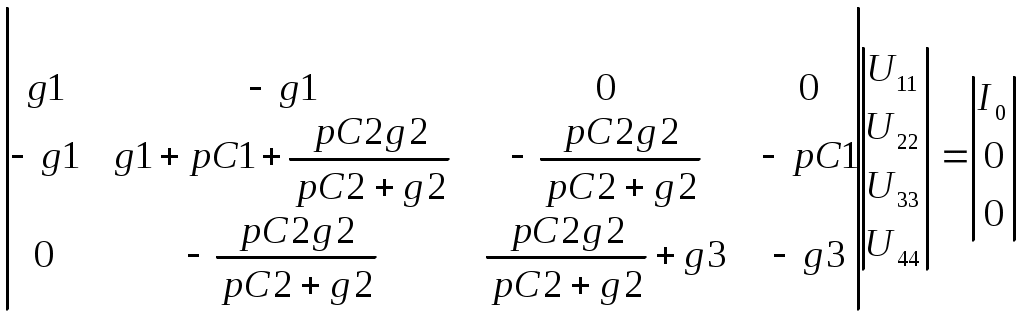 (1.1) (1.1)Рассмотрим основное уравнение операционного усилителя: Так как величина К= 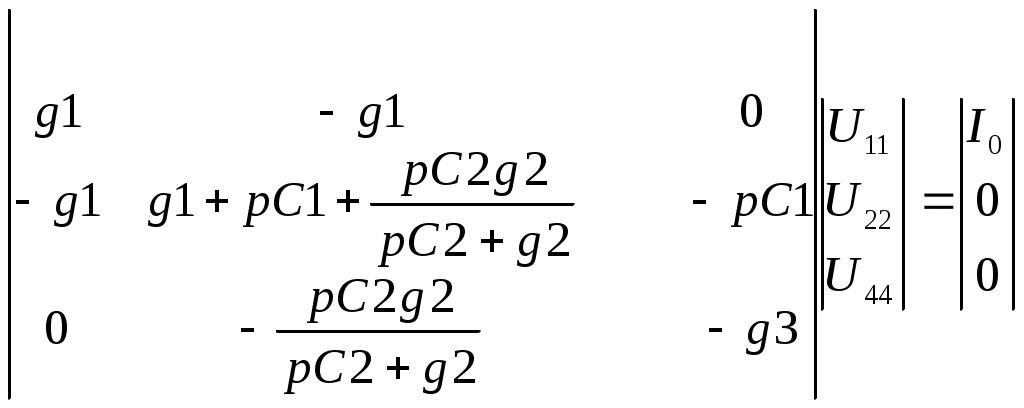 (1.3) (1.3)Функцию коэффициента передачи по напряжению определяем как отношение выходного напряжения ко входному. Согласно методу Крамера входное и выходное напряжения определяются: Подставим (1.6) и (1.5) в (1.4): Подставляем значения номиналов элементов: R1=R2=100 Ом, R3=1 MОм, С1=С2=0,01 мкФ. Функцию входного сопротивления определяем как отношение входного напряжения к входному току. Находим: Подставим (1.6) и (1.10) в (1.9): Подставляем значения номиналов элементов: R1=R2=100 Ом, R3=1 MОм, С1=С2=0,01 мкФ. 2. Построение карты особых точек. Произведем расчет нулей и полюсов функции коэффициента передачи по напряжению, которая задана в виде отношения полиномов: Функция коэффициента передачи по напряжению имеет два простых нуля: Рассчитаем полюсы. Строим карту особых точек функции Кu(jw): 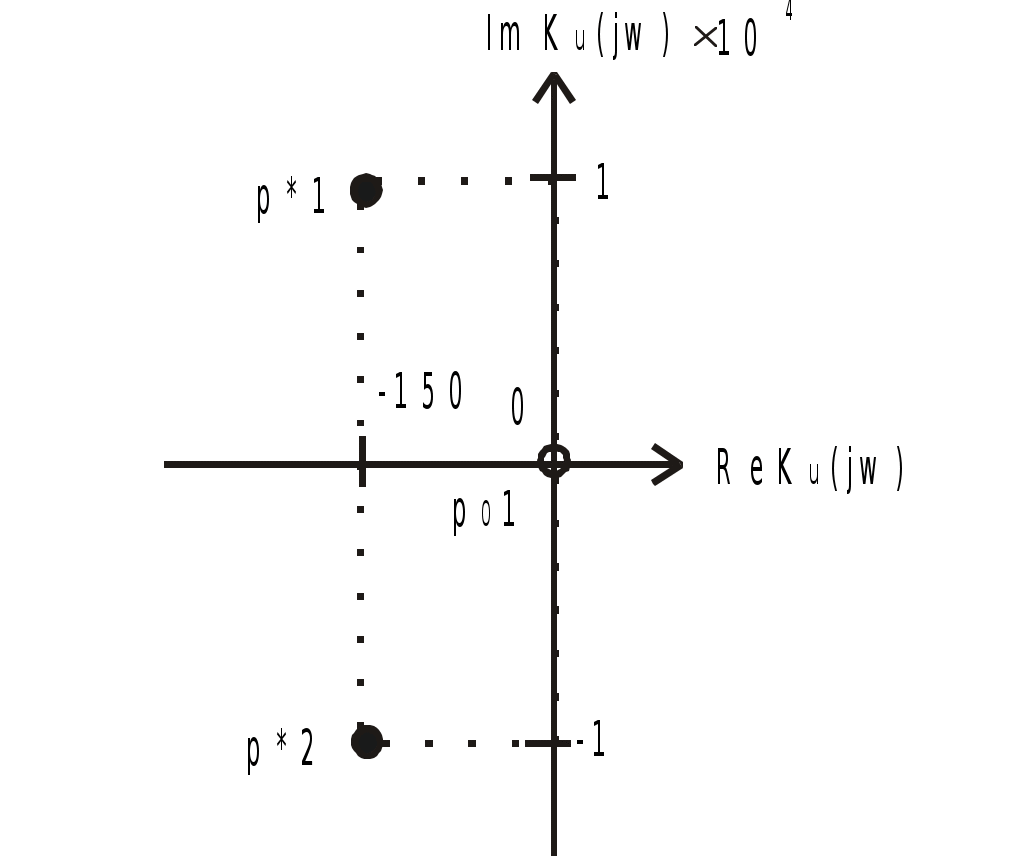 Рис. 2.1. Полюсно-нулевая карта Ku(p). Коэффициент передачи по напряжению имеет два простых нуля, лежащих на действительной оси и два комплексно-сопряженных полюса. Произведем расчет нулей и полюсов функции входного сопротивления: Рассчитаем нули. Рассчитаем полюсы: Строим карту особых точек функции Z11(jw): 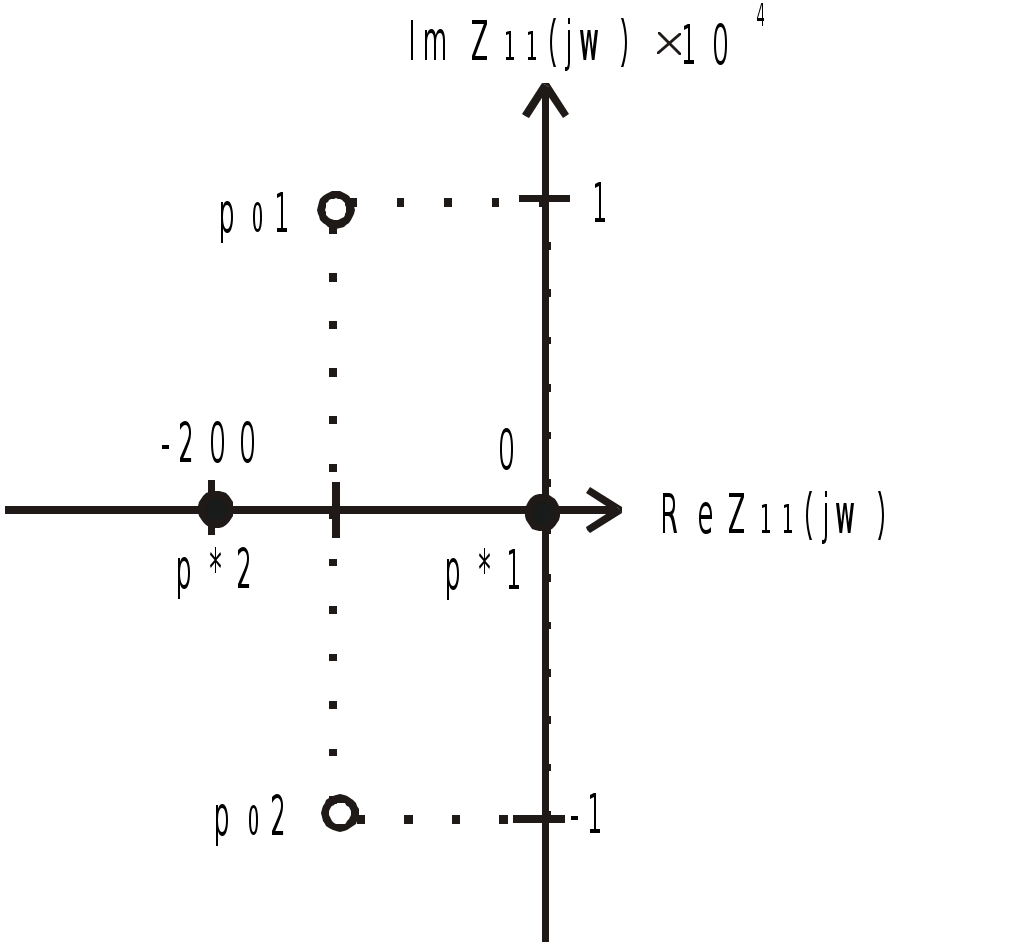 Рис. 2.1. Полюсно-нулевая карта Z11(p). Функция входного сопротивления имеет два простых полюса, лежащих на действительной оси и два комплексно-сопряженных нуля. 3. Расчет и построение частотных характеристик. Для расчета АЧХ и ФЧХ необходимо вычислить модуль и аргумент комплексных функций (1.8) и (1.12). Для этого необходимо заменить операторную переменную р=j: Определим модули выражений (3.1) и (3.2): Определим аргументы выражений (3.1) и (3.2). Поскольку при расчете аргументов комплексных чисел через функцию арктангенса необходимо учитывать особые точки, то выражение для аргумента будет представлять собой систему уравнений. 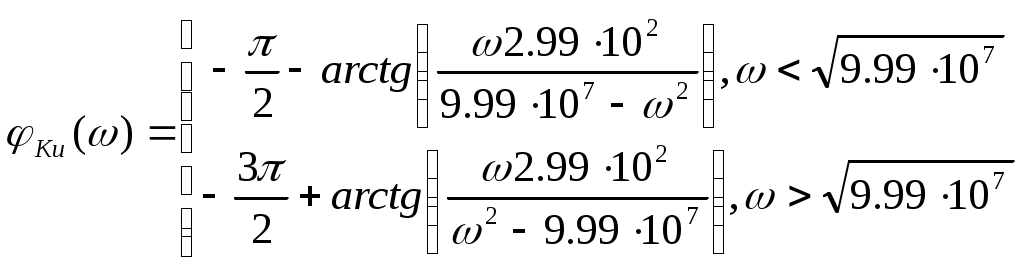 (3.5) (3.5)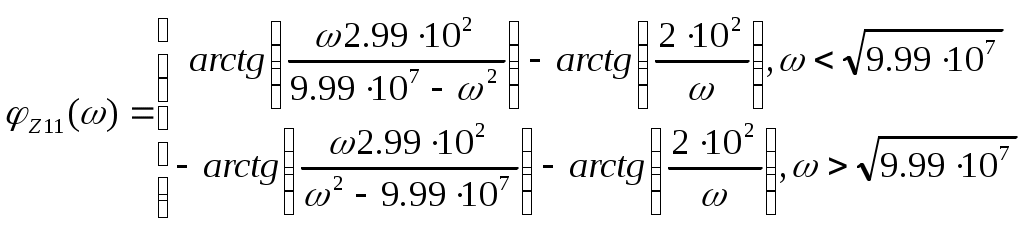 (3.6) Годограф определяет положение конца вращающегося вектора коэффициента передачи на комплексной плоскости. Для построения АФХ (годографа) функции коэффициента передачи по напряжению и входного сопротивления в декартовой системе координат необходимо составить уравнения связи: 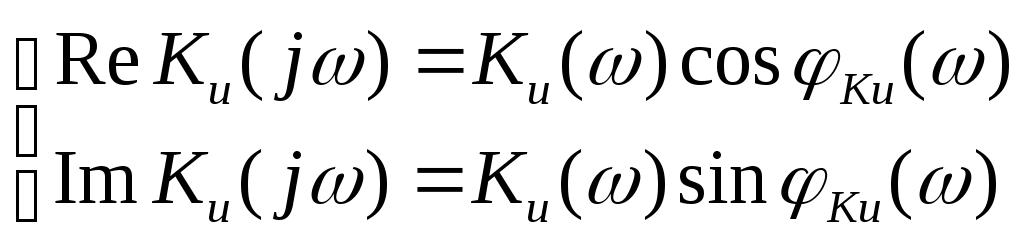 (3.7) (3.7)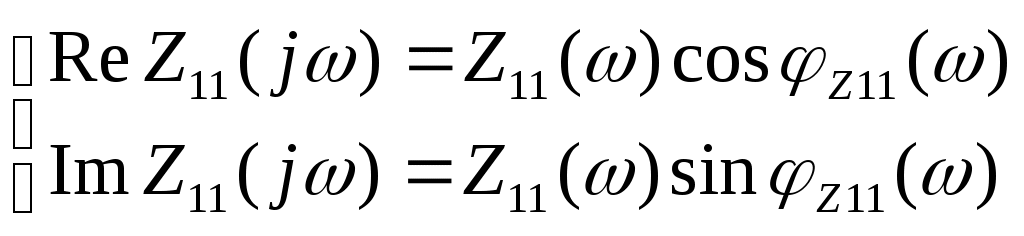 (3.8) (3.8)Производим расчет значений выражений (3.2) - (3.8). Данные вычислений помещены в таблицу 3.1 и таблицу 3.2. Таблица 3.1. 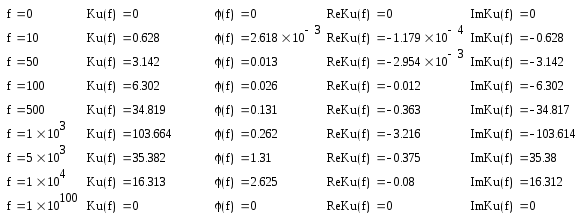 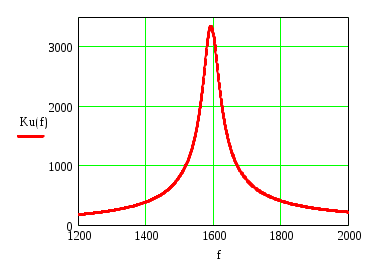 Рис. 3.1. АЧХ коэффициента передачи по напряжению. 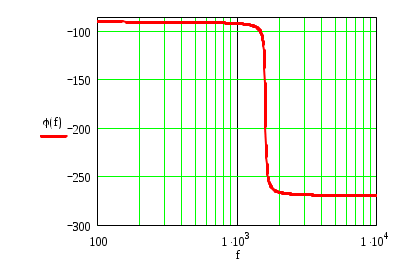 Рис. 3.2. ФЧХ коэффициента передачи по напряжению. 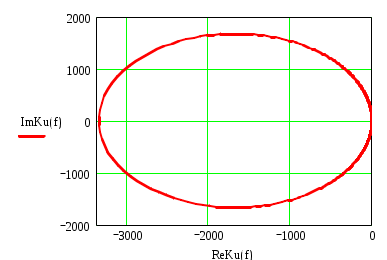 Рис. 3.3. АФХ коэффициента передачи по напряжению. Таблица 3.2. 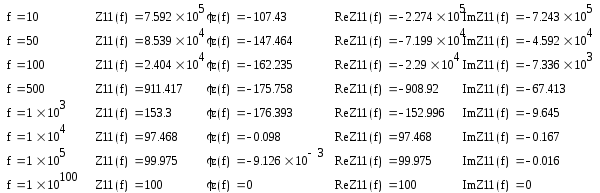 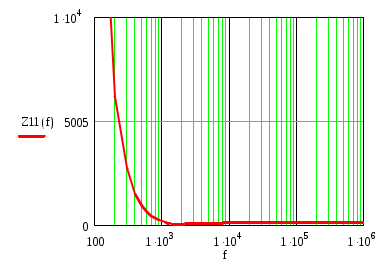 Рис. 3.4. АЧХ входного сопротивления. 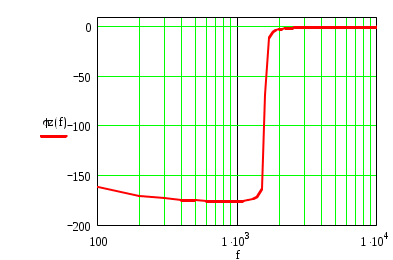 Рис. 3.5. ФЧХ входного сопротивления. 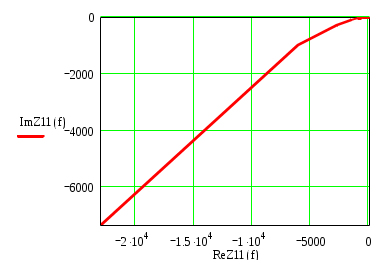 Рис. 3.6. АФХ входного сопротивления. 4. Расчет и построение переходных характеристик. Определим переходную характеристику выходного напряжения. По таблицам обратного преобразования Лапласа находим оригинал функции (4.2): Переходная характеристика входного напряжения при условии подачи на вход скачка тока величиной 1 мА: Iвх=10-31(t) равна: По таблицам обратного преобразования Лапласа находим: Производим расчет по формулам (4.3) и (4.8). Данные помещены в таблицу 4.1. Таблица 4.1. 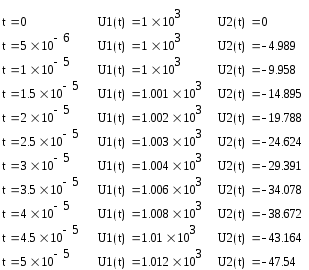 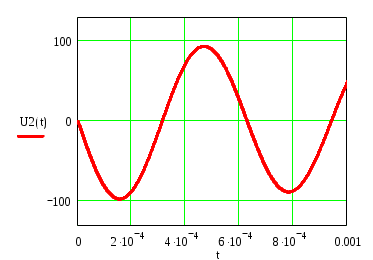 Рис. 4.1. Переходная характеристика выходного напряжения. 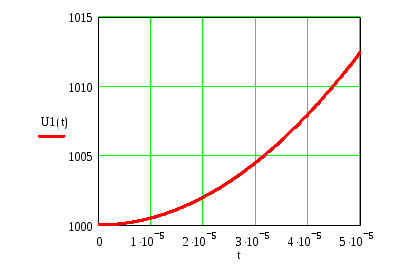 Рис. 4.2. Переходная характеристика входного напряжения. Выводы. Данный фильтр по типу частотной характеристики представляет собой полосовой фильтр (ПФ). На нулевой частоте коэффициент передачи фильтра равен нулю, так как сопротивление конденсаторов С1 и С2 равно бесконечности. На средних частотах коэффициент передачи фильтра определяется суммарным сопротивлением цепи С1,R1,С2,R2 и резистором обратной связи R3. На высоких частотах сопротивление конденсаторов становится равным нулю и, поэтому, коэффициент передачи определяется резисторами R1 и R2. Переходная характеристика выходного напряжения представляет собой сумму затухающих гармонических составляющих. Список литературы 1. Попов В. П. Основы теории цепей. М. "Высшая школа", 1985 г. 2. Матханов П. Н. Основы анализа электрических цепей. Линейные цепи М. "Высшая школа", 1990 г. 3. Шебес М. Р. Задачник по теории линейных электрических цепей. М. "Высшая школа", 1990 г. 4. Лосев А. К. Теория линейных электрических цепей. М. "Высшая школа", 1987 г. |
