Курсовая по информатике. Исследование численных методов вычисления определенных интегралов
 Скачать 235.79 Kb. Скачать 235.79 Kb.
|
|
Государственное образовательное учреждение высшего профессионального образования «Тверской государственный технический университет» (ГОУВПО «ТвГТУ») Кафедра информатики и прикладной математики Курсовая работа по дисциплине "Информатика" на тему: Исследование численных методов вычисления определенных интегралов Выполнил: студент группы Номер зачетной книжки: Проверил: Тверь 2020 ОглавлениеВведение 3 Теоретическая часть 5 Расчётная часть 18 Заключение 24 Список использованной литературы 25 ВведениеСовременное развитие физики и техники тесно связано с использованием электронных вычислительных машин (ЭВМ). В настоящее время ЭВМ стали обычным оборудованием многих институтов и конструкторских бюро. Это позволило от простейших расчетов и оценок различных конструкций или процессов перейти к новой стадии работы - детальному математическому моделированию (вычислительному эксперименту), которое существенно сокращает потребность в натурных экспериментах, а в ряде случаев может их заменить. Сложные вычислительные задачи, возникающие при исследовании физических и технических проблем, можно разбить на ряд элементарных -таких как вычисление интеграла, решение дифференциального уравнения и т. п. Многие элементарные задачи являются несложными и хорошо изучены. Для этих задач уже разработаны методы численного решения, и нередко имеются стандартные программы решения их на ЭВМ. Есть и достаточно сложные элементарные задачи; методы решения таких задач сейчас интенсивно разрабатываются. В связи с этим современный специалист с высшим образованием должен обладать не только высоким уровнем подготовки по профилю своей специальности, но и хорошо знать математические методы решения инженерных задач, ориентироваться на использование вычислительной техники, практически освоить принципы работы на ЭВМ. Цель данной курсовой работы – изучение методов приближённого интегрирования. Для некоторых подынтегральных функций интеграл можно вычислить аналитически или найти в справочниках. Однако в общем случае первообразная может быть не определена: либо первообразные не выражаются через элементарные функции, либо сами подынтегральные функции не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов. Наиболее общеупотребительными приближенными методами вычисления одномерных определенных интегралов являются, так называемые, "классические" методы численного интегрирования: метод прямоугольников, метод трапеций, метод парабол (основанные на суммировании элементарных площадей, на которые разбивается вся площадь под функцией). Хотя эти методы обычно предпочтительней в случае малых размерностей, они практически не годятся для вычисления многомерных интегралов, для их вычисления используются другие методы, однако в этой работе они рассмотрены не будут. Теоретическая частьЧисленное интегрирование Постановка задачи Пусть требуется вычислить определенный интеграл 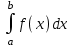 , (1) , (1)где f(x) – непрерывная на отрезке [a; b] функция. С геометрической точки зрения интеграл (1) при f(x) > 0 равен площади криволинейной трапеции, ограниченной кривой y = f(x), осью Oxи прямыми x = a, x = b(рис. 1). Другими словами, 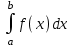 равен площади заштрихованной фигуры на рис. 1. равен площади заштрихованной фигуры на рис. 1.Р  ис. 1. Геометрический смысл определенного интеграла. Вычислить определенный интеграл (1) можно с помощью аналитической формулы Ньютона-Лейбница (2):  , (2) , (2)где F(x) – первообразная функция для заданной функции f(x). Однако во многих случаях не удается найти никакой аналитической формулы в виду невозможности определения F(x). Таким интегралом, например, является  . (3) . (3)В математическом анализе доказывается, что для данной подынтегральной функции нельзя выразить первообразную F(x) через элементарные функции. С другой стороны площадь криволинейной трапеции, задаваемой интегралом (3) существует (рис. 3). Значит, должно существовать и значение интеграла, которое, однако, мы не можем найти точно. 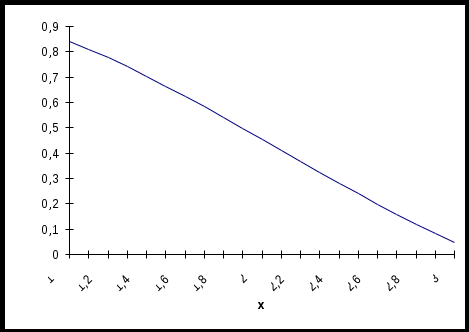 Рис. 2. График функции  на отрезке [1; 3]. на отрезке [1; 3].В таких случаях приходится применять методы численного интегрирования. Основной принцип построения всех приближенных формул численного интегрирования состоит в том, что интервал интегрирования разбивается на множество меньших отрезков, внутри которых подынтегральная кривая y = f(x) заменяется с некоторой степенью точности более простыми функциями, интегралы от которых можно вычислить. С геометрической точки зрения выполняется следующее: искомая площадь криволинейной трапеции приближенно заменяется суммой площадей элементарных геометрических фигур. Метод прямоугольников. Как говорилось выше, вычисление интеграла  равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x = a, x = bи «боковыми сторонами» y = 0, y = f(x) (рис. 1). равносильно вычислению площади некоторой фигуры – криволинейной трапеции с параллельными «основаниями» x = a, x = bи «боковыми сторонами» y = 0, y = f(x) (рис. 1).Разобьем интервал интегрирования на n равных частей, каждая длиной  . .Приближенное значение интеграла получается в виде суммы площадей n прямоугольников, высота которых равна значению f(x) на левом краю каждого подинтервала (рис. 3).   hy0+hy1+…+hyn-1 = h(y0+y1+…+yn-1). То есть формула численного интегрирования имеет вид: hy0+hy1+…+hyn-1 = h(y0+y1+…+yn-1). То есть формула численного интегрирования имеет вид: (4) (4)и называется формулой «левых» прямоугольников.  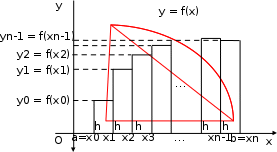 Рис. 3. Геометрическая интерпретация метода «левых» прямоугольников. Если в качестве приближенного значения площади для каждого подинтервала принять площадь прямоугольника, высота которого равна значению f(x) на правом краю подинтервала (рис. 4), то формула численного интегрирования имеет вид (5):  (5) (5)и называ  ется формулой «правых» прямоугольников. Рис. 4. Геометрическая интерпретация метода «правых» прямоугольников. Существует третья модификация метода прямоугольников – метод «средних» прямоугольников. В этом случае в качестве приближенного значения площади для каждого подинтервала принимается площадь прямоугольника, высота которого равна значению f(x) в средней точке подинтервала (рис. 5). Р 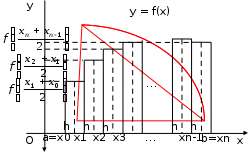 ис. 5. Геометрическая интерпретация метода «средних» прямоугольников. Тогда формула численного интегрирования имеет вид (6):  (6) (6)Метод прямоугольников – это наиболее простой и вместе с тем наиболее грубый метод приближенного интегрирования. Очевидно, что чем больше будет число n отрезков разбиения, тем более точный результат дадут формулы (4)-(6). Однако увеличение числа отрезков разбиения промежутка интегрирования не всегда возможно. Поэтому большой интерес представляют формулы, дающие более точные результаты при том же числе точек разбиения. Заметно меньшую погрешность дает другой метод – метод трапеций. Метод трапеций В этом методе отрезок [a; b] так же разбивается на nравных частей. На каждом отрезке [xi; xi+1] кривая y = f(x) заменяется прямой, проходящей через две известные точки с координатами  и и  , где , где и строится прямоугольная трапеция с высотой и строится прямоугольная трапеция с высотой  (рис. 6). (рис. 6). Рис. 6. Геометрическая интерпретация метода трапеций. В итоге искомая площадь криволинейной трапеции приближенно заменяется суммой площадей элементарных геометрических трапеций. (Площадь трапеции с высотой h и основаниями a, b вычисляется по формуле:  ). Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников. ). Из геометрических соображений понятно, что площадь такой фигуры будет, вообще говоря, более точно выражать площадь криволинейной трапеции, нежели площадь ступенчатой фигуры, рассматриваемая в методе прямоугольников.Тогда   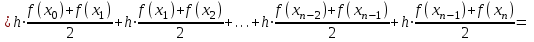 вынесем h за скобку, получим  разобьем каждую дробь на две дроби  приведем подобные слагаемые, получим 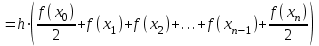 . .Итак,   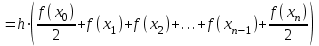 . .Коротко полученную формулу можно записать в виде (7).    (7) (7)Заметим, что в данном методе получаем ступенчатую фигуру, составленную из трапеций, которая «плотнее» прилегает к заданной криволинейной трапеции, нежели фигура, составленная из прямоугольников в предыдущем методе. Метод парабол (Симпсона) Значительное повышение точности приближенных формул численного интегрирования дает метод парабол (Симпсона). Идея метода исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает кривой y = f(x), чем хорда, соединяющая концы дуги этой кривой (метод трапеций). Поэтому значения площадей соответствующих элементарных трапеций, ограниченных сверху дугами парабол, являются более близкими к значениям площадей соответствующих 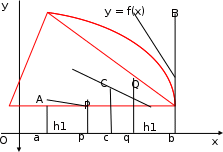 частичных криволинейных трапеций, ограниченных сверху дугой кривой y = f(x), чем значения площадей соответствующих прямолинейных трапеций. Рис. 7. Геометрическая интерпретация метода парабол. Рассмотрим функцию y = f(x). Будем считать, что на отрезке [a; b] она положительна и непрерывна. Найдем площадь криволинейной трапеции aABb (рис. 7). Для этого разделим отрезок [a, b] точкой c =  пополам и в точке C(c, f(c)) проведем касательную к линии y = f(x). После этого разделим [a, b] точками p и q на три равные части и проведем через них прямые x = p и x = q. Пусть P и Q – точки пересечения этих прямых с касательной. Соединив A с P и B с Q, получим три прямолинейные трапеции aAPp, pPQq, qQBb. Тогда площадь трапеции aABb можно приближенно посчитать по следующей формуле пополам и в точке C(c, f(c)) проведем касательную к линии y = f(x). После этого разделим [a, b] точками p и q на три равные части и проведем через них прямые x = p и x = q. Пусть P и Q – точки пересечения этих прямых с касательной. Соединив A с P и B с Q, получим три прямолинейные трапеции aAPp, pPQq, qQBb. Тогда площадь трапеции aABb можно приближенно посчитать по следующей формуле  , ,где  . .Откуда получаем  . .Заметим, что aA = f(a),bB = f(b),а pP + qQ = 2f(c) (как средняя линия трапеции), в итоге получаем малую формулу Симпсона  (8) (8)В данном случае дуга ACBзаменяется параболой, проходящей через точки A, P, Q, B. Малая формула Симпсона дает интеграл с хорошей точностью, когда график подынтегральной функции мало изогнут, в случаях же, когда дана более сложная функция, малая формула Симпсона непригодна. Тогда, чтобы посчитать интеграл заданной функции нужно разбить отрезок [a, b] на n частей и к каждому из отрезков применить формулу (8). Обязательным требованием, вытекающим из геометрического смысла метода парабол, является то, что n должно быть четным. Пусть  , точки деления будут х0=а, x1, x2, …xn-2, xn-1, xn=b, а y0, y1, …yn – соответствующие значения подынтегральной функции на отрезке [a, b]. , точки деления будут х0=а, x1, x2, …xn-2, xn-1, xn=b, а y0, y1, …yn – соответствующие значения подынтегральной функции на отрезке [a, b].Тогда, применяя малую формулу Симпсона к каждой паре получившихся отрезков, имеем  Тогда  . (9) . (9)Заметим, что во всех выражениях  первый множитель равен первый множитель равен 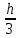 : : (10) (10)Сделав замену по формулам (10), вынося общий множитель 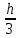 за скобку, в (9) получаем: за скобку, в (9) получаем: 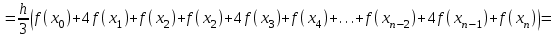 группируем слагаемые  . .Таким образом, получаем «большую» формулу Симпсона, которая имеет вид: 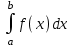  (11) (11)Предлагаем для запоминания следующий вид формулы: 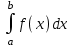  (11’) (11’)где Yкр = y0 + yn, Yнеч = y1 + y3 + … + yn-1, Yчет = y2 + y4 + … + yn-2, а  . .Правило Рунге оценки погрешности В каждой конкретной задаче необходимо определить число точек деления n, необходимое для вычисления интеграла (1) с требуемой точностью ε. Для определения n удобно следующее правило Рунге. Пусть ε – заданная точность вычисления интеграла (1), тогда шаг h должен удовлетворять условию 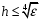 (12) (12)По этому значению h из соотношения  определяется n. При этом для метода Симпсона в качестве n берется ближайшее четное целое число, превосходящее определяется n. При этом для метода Симпсона в качестве n берется ближайшее четное целое число, превосходящее  , а для методов прямоугольников и трапеций – ближайшее целое, превосходящее , а для методов прямоугольников и трапеций – ближайшее целое, превосходящее . .Оценку погрешности можно провести также следующим методом Рунге. Пусть  - приближенное значение интеграла (1), вычисленное с шагом h, а - приближенное значение интеграла (1), вычисленное с шагом h, а  - значение этого интеграла, вычисленное с шагом 2h. Заметим, что чем меньше шаг h (а, следовательно, больше n), тем точнее получается приближенное значение интеграла. - значение этого интеграла, вычисленное с шагом 2h. Заметим, что чем меньше шаг h (а, следовательно, больше n), тем точнее получается приближенное значение интеграла.Если  , (13) , (13)где  и и  вычислены по методу Симпсона, или вычислены по методу Симпсона, или , (14) , (14)где  и и  вычислены по методу прямоугольников или трапеций, то в качестве приближенного значения интеграла (1) берут значение вычислены по методу прямоугольников или трапеций, то в качестве приближенного значения интеграла (1) берут значение  . .Если неравенство для соответствующего метода не выполняется, то найденное значение интеграла не удовлетворяет заданной точности. Тогда проводят новые вычисления с шагом 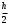 и вновь проверяют выполнение неравенства (13) или (14). Этот прием многократного уменьшения шага применяют до тех пор, пока соответствующее неравенство не станет истинным. и вновь проверяют выполнение неравенства (13) или (14). Этот прием многократного уменьшения шага применяют до тех пор, пока соответствующее неравенство не станет истинным.Расчётная частьВариант 14 Задача: вычислить разными методами интеграл: 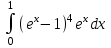 Точность: 0,0001 Вычисление аналитически Используем интегрирование по частям:  Вычисление численными методами: Оценим величину шага h по формуле: 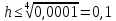 Определяем количество значений: 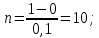 Принимаем n = 10 Уточняем шаг:  Определяем значение интеграла с заданным шагам методами правых прямоугольников, левых прямоугольников, средних прямоугольников, трапеций и парабол (метод Симсона) с использованием Excel.
График заданной функции с шагом 0,1 представлен на рисунке 7  Рис. 7 – График функции для шага 0,1 Определяем значения интеграла для шага 2h = 0,2. Оцениваем погрешность по методу Рунге
График заданной функции с шагом 0,2 представлен на рисунке 8 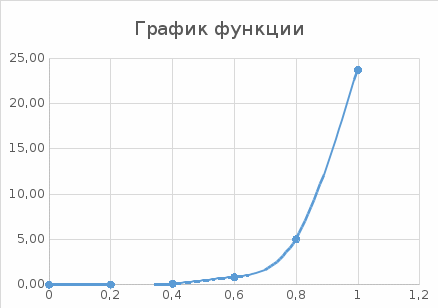 Рис. 8 – График функции для шага 0,2 Погрешность по Рунге с использованием метода Симсона значительно превышает заданную точность, поэтому уменьшаем исходный шаг до h/2 = 0,05 и интегралы, а также точность по методу Рунге.
График заданной функции с шагом 0,05 представлен на рисунке 9  Рис. 9 – График функции для шага 0,05 Погрешность по методу Рунге для определения интеграла с шагом 0,05 методом парабол равна 0,0003. Выводы: По оценке точности как абсолютного значения разности значения аналитического значения интеграла и значения, рассчитанного численными методами, самым точным методом оказался метод Сисмсона. Следующий по точности метод – метод средних прямоугольников. Далее – метод трапеций; При уменьшении шага численного интегрирования в 2 раза точность определения интеграла методом правых прямоугольников увеличилась в 2,1 раза; При уменьшении шага численного интегрирования в 2 раза точность определения интеграла методом левых прямоугольников увеличилась в 1,87 раза; При уменьшении шага численного интегрирования в 2 раза точность определения интеграла методом средних прямоугольников увеличилась в 3,96 раза; При уменьшении шага численного интегрирования в 2 раза точность определения интеграла методом трапеций увеличилась в 3,98 раза; При уменьшении шага численного интегрирования в 2 раза точность определения интеграла методом парабол увеличилась в 15,5 раз; ЗаключениеСложные вычислительные задачи, возникающие при исследовании физических и технических проблем, можно разбить на ряд элементарных -таких как вычисление интеграла, решение дифференциального уравнения и т. п. Многие элементарные задачи являются несложными и хорошо изучены. Для этих задач уже разработаны методы численного решения, и нередко имеются стандартные программы решения их на ЭВМ. Есть и достаточно сложные элементарные задачи; методы решения таких задач сейчас интенсивно разрабатываются. В связи с этим современный специалист с высшим образованием должен обладать не только высоким уровнем подготовки по профилю своей специальности, но и хорошо знать математические методы решения инженерных задач, ориентироваться на использование вычислительной техники, практически освоить принципы работы на ЭВМ. В процессе проведённой работы мною были изучены численные методы интегрирования с использованием программы Microsoft Excel. Список использованной литературыКаханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение (пер. с англ.). М.: Мир, 2001, 575 c. ISBN 5-03-003392-0. Самарский А. А., Гулин А. В. Численные методы: Учеб. пособие для вузов. — М.: Наука. Гл. ред. физ-мат. лит., 1989. — 432 с. ISBN 5-02-013996-3. Пискунов Н. С. Дифференциальное и интегральное исчисления для вузов. — 13-е изд. — М.: Наука. Гл. ред. физ-мат. лит., 1985. — 432 с. |
