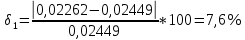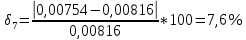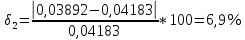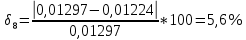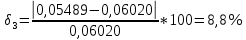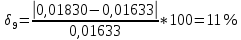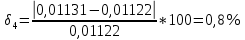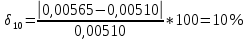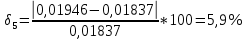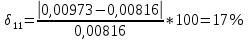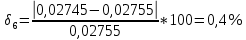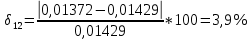Лабораторная 304. Исследование дифракции фраунгофера санктпетербург 2023
 Скачать 321.59 Kb.
|
|
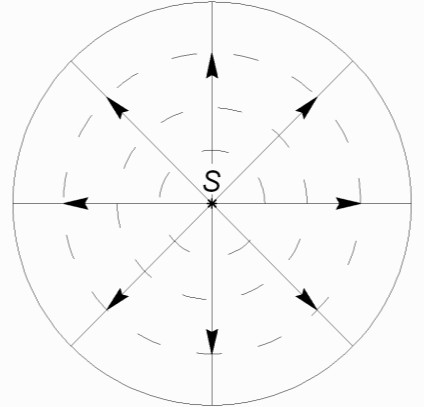
Государственное образовательное учреждение высшего профессионального образования «ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» Кафедра «Физика» ИССЛЕДОВАНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА САНКТ-ПЕТЕРБУРГ 2023 Целью лабораторной работы является:визуальное наблюдение на экране картины дифракции плоской световой волны на щели; изучение влияния ширины щели на расположение дифракционных максимумов; экспериментальное определение углов дифракции, соответствующих максимумам интенсивности света на экране, и сравнение их с теоретическими углами дифракции. Дифракция Фраунгофера на щелиСветом называют электромагнитные волны, т.е. процесс распространения в вакууме или диэлектрической среде электромагнитных колебаний. Источниками электромагнитных волн являются возбужденные атомы или молекулы. Длины волн видимой области электромагнитного излучения лежат в интервале от 400 до 750 нм. Геометрическое место точек, до которых к моменту времени t доходят электромагнитные колебания от источника света, называется фронтом световойволны. Геометрическое место точек, в которых колебания происходят в одинаковой фазе, называется волновойповерхностью. В вакууме или изотропной однородной среде скорость Vраспространения колебаний одинакова для любого направления, поэтому (Рис.1) от точечного источника света Sза время t колебания дойдут до точек, образующих поверхность сферы радиуса R=V·t.Фронт волны представляет собой поверхность сферы, поэтому такая волна называется сферической.
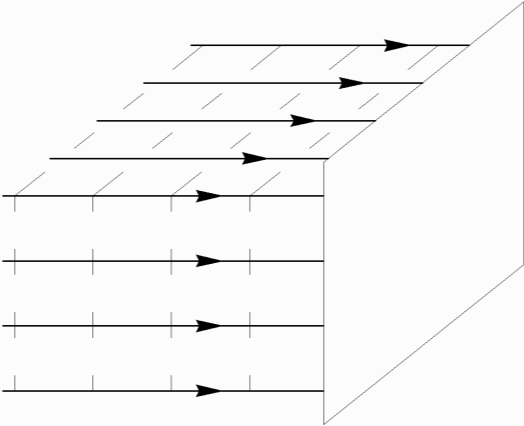
С увеличением расстояния от точечного источника света кривизна сферического фронта уменьшается. Небольшой участок волнового фронта достаточно большого радиуса Rможно считать плоскимфронтом, лучи (направления распространения колебаний) – идущими параллельно друг другу. Такую световую волну называют плоскойволной (Рис.2). Плоскую световую волну (пучок параллельных лучей) можно получить с помощью оптических систем. Отклонение световых лучей от прямолинейного распространения при прохождении в среде с резко неоднородной пропускающей способностью называется дифракциейсвета. Не очень строго дифракцией называют огибание волнами препятствий, в результате чего граница тени от предмета становится размытой. Характерную картину дифракции можно наблюдать при прохождении света через малые отверстия, вблизи краев экрана, непрозрачных препятствий малых размеров и других неоднородностей (Рис.3, рис.4).
Дифракцию, наблюдаемую в параллельных лучах (случай плоской волны), называют дифракциейФраунгофера. Если падающие на объект лучи непараллельны друг другу (сферическая волна), то говорят о дифракцииФренеля. 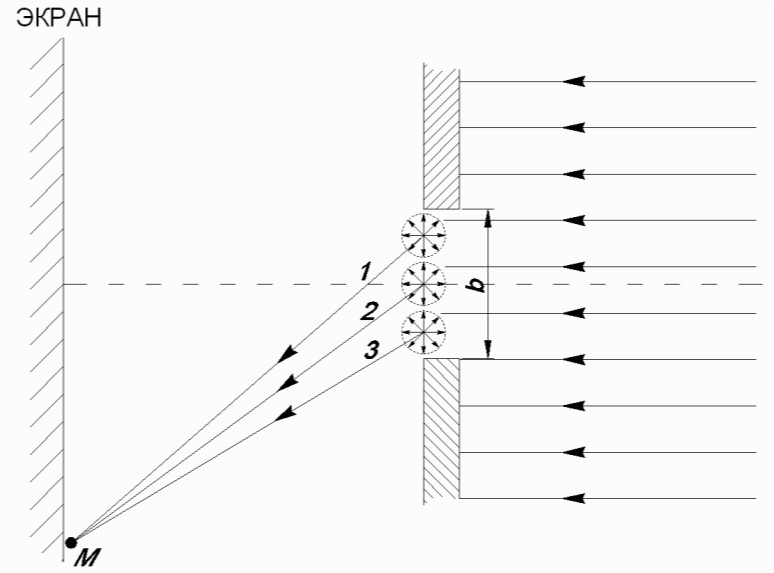 Рис. 5 Строгое решение задачи дифракции очень сложно. Достаточно хорошие результаты для объяснения этого явления в оптических задачах дает использование принципаГюйгенса–Френеля. Согласно этому принципу точкифронтаволны являются когерентнымиисточниками вторичных сферическихволн. На рис.5 изображен пучок параллельных световых лучей, падающий нормально (перпендикулярно) на щель шириной b и дающий на экране, помещенном за щелью, дифракционную картину. Освещенность экрана в точке Mопределяется результатом интерференции колебаний от всех вторичных источников – точек участка фронта волны, вырезанного щелью. Точечные источники изображены символом  . На рис.5 показано для примера, что интерферируют колебания, идущие вдоль лучей 1,2и 3.Свет наблюдается в тех местах экрана, где вторичные волны при интерференции негасят друг друга. Интенсивность дифрагированной волны максимальна там, где колебания складываясь, усиливаются, и на экране возникает дифракционный максимум света – светлое пятно. В тех точках экрана, где колебания складываясь, гасят друг друга, наблюдается темнота, т.е. дифракционный минимум. 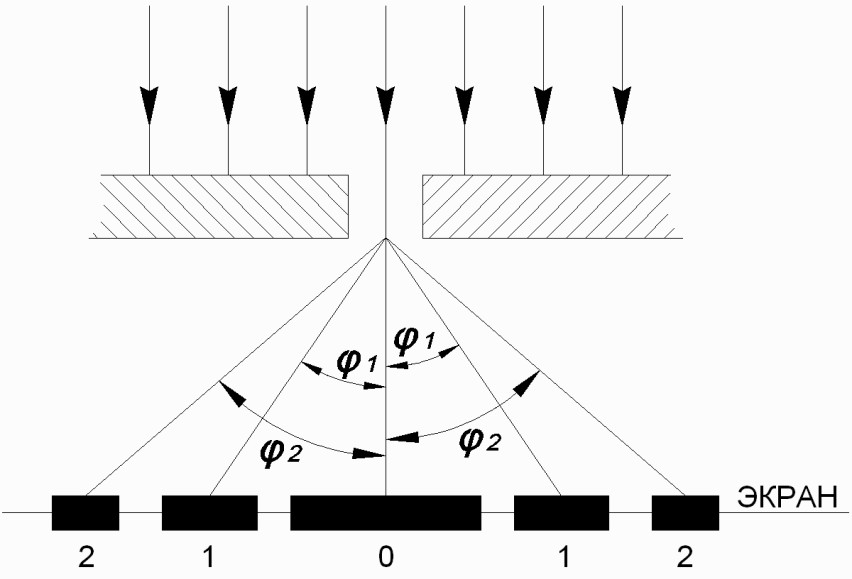 Рис. 6 На экране (Рис.6) наблюдаются несколько максимумов и минимумов освещенности справа и слева от центрального светлого «нулевого» пятна. Углом дифракции φmaxназывают угол между направлением падающих лучей и лучом, проведенным от середины щели к точке на экране, где находится середина максимума освещенности. Зависимость интенсивности света Iφв разных точках экрана дается формулой (см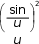. [1]):   , (1)где I0– интенсивность в центре экрана, 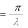 u b sin , (2)b– ширина щели, λ – длина волны. Для определения углов дифракции исследуем на экстремум функцию Iφ. Взяв производную по uи приравняв ее нулю, получаем: 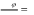 dI 2Idu sin u 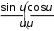 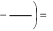 0 u20 . (3) Выражение (3) распадается на два уравнения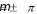:  sin u 0 ,uu tgu. (4)   Первое из них определяет положения минимумов интенсивности (Iφ = 0), которые будут иметь место при u , где m1, 2, 3 …, (5) т.е. при углах дифракции (см.(2)), удовлетворяющих условию: 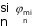 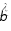 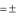 m , где m=1, 2, 3 … (6)Второе уравнение дает положения максимумов интенсивности при значениях u= 0; 1,43π; 2,46π; 3,47π … (7) Для углов φ, учитывая (2) получаем: Для малых углов 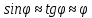 sin sin sin  1max 2 max 3 max1,43 b,     2,46 b, (8) 3,47 b,(рад), поэтому можно вычислить теоретическиезначенияугловдифракцииврадианах по формулам: 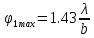 ;  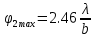;  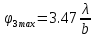(9)График зависимости интенсивности света Iφ от sin  или угла φ,выраженного в радианах, показан на рис.7. 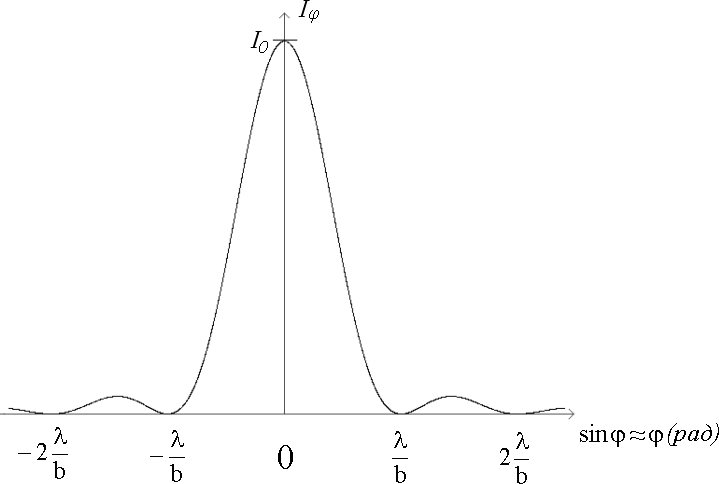 Рис. 7 При u=0 интенсивность света максимальна (Iφ= I0) и не зависит от 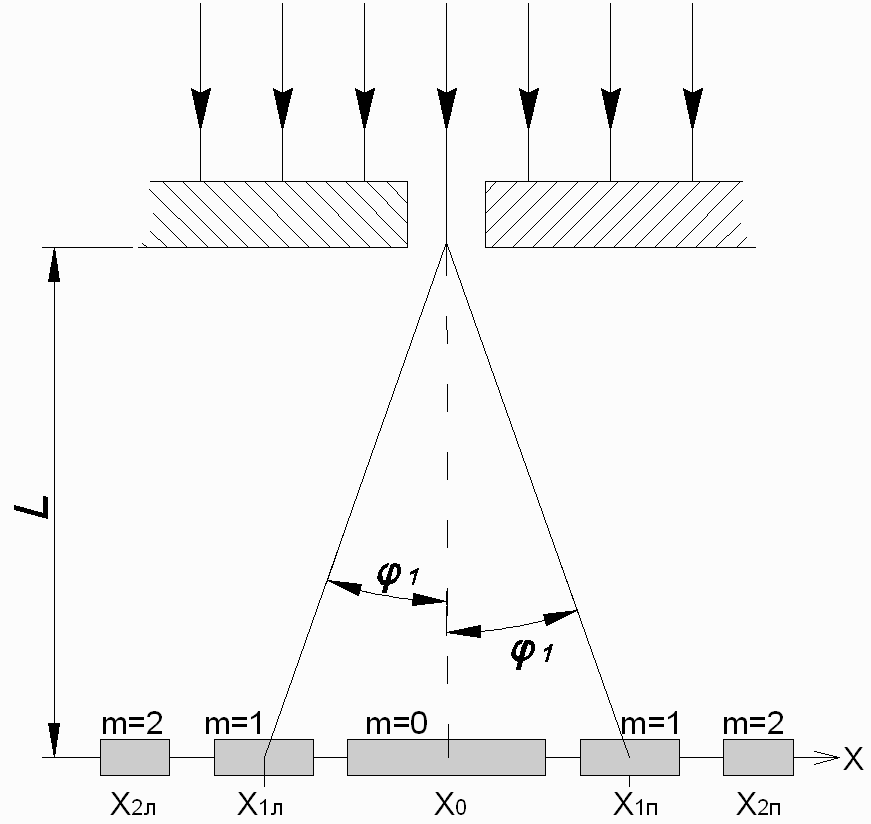 Рис. 8 длины волны. Иными словами, в направлении падающего на щель излучения (φ=0) всегда расположен максимум. Этот центральный максимум называют максимумом нулевогопорядка. Для нахождения угла дифракции φ1, под которым виден максимум первогопорядка (m=1), необходимо по шкале xна экране (Рис.8) определить положения максимумов первого порядка слева (x1л) и справа (x1п) (например, x1л=10 мм, x1п=11) мм и, измерив L- расстояние от щели до экрана (например, L= 400 мм), определить: 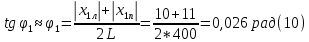 Аналогичным образом находят углы дифракции для максимумов второго и следующих порядков. Описание установки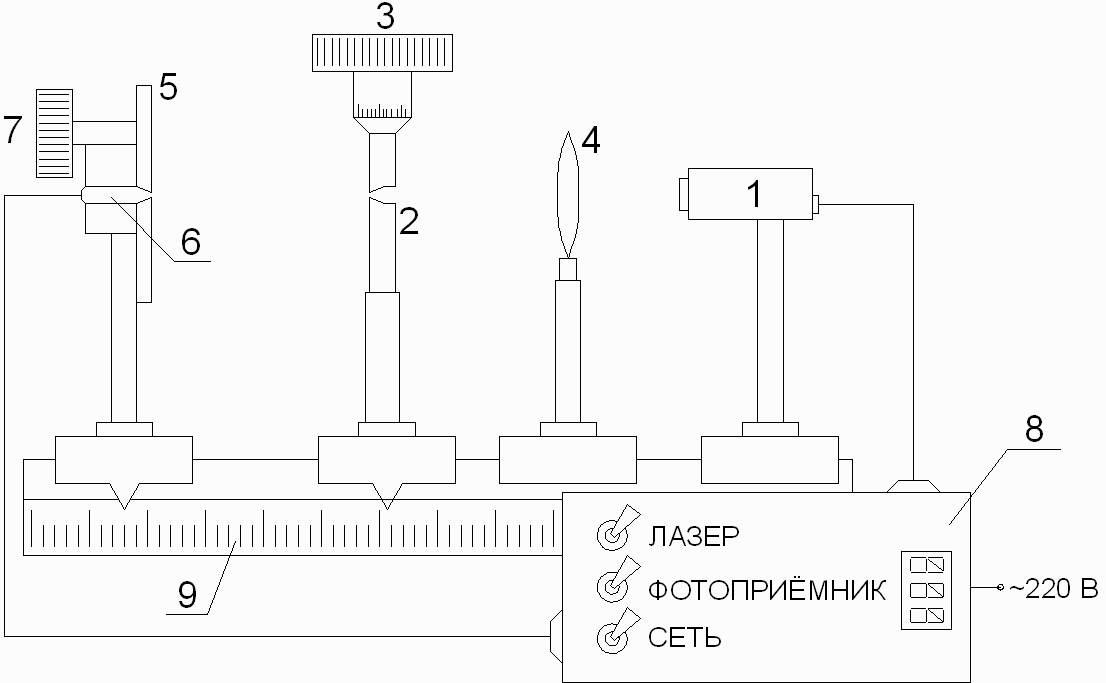 Схема установки для наблюдения дифракции монохроматической плоской волны на щели представлена на рис.9.Рис. 9 На оптической скамье установлены: – полупроводниковый лазер, дающий монохроматическое излучение λ=632,8 нм; – щель с регулируемой и измеряемой с помощью микрометра 3шириной; цена деления микрометра 0,01 мм. – длиннофокусная линза для концентрации света на щели; – экран; – фотоприемник, установленный за экраном против миллиметрового отверстия и соединенный с чувствительным гальванометром, находящимся в блоке 8; на верхней панели блока расположены тумблеры включения сетевого напряжения, лазера и фотоприемника (фотоприемник в данной работе используется только по указанию преподавателя); –рукоятка перемещения экрана; с помощью этой рукоятки центр экрана наводят на середину соответствующего максимума и определяют по шкале его положение; цена деления шкалы на экране – 1мм; 9– линейка для определения расстояния от щели до экрана. Порядок выполнения работыВставить сетевую вилку блока 8в розетку. Включить тумблеры «СЕТЬ» и «ЛАЗЕР», убедиться, что возникло лазерное свечение. Проверить и, если необходимо, откорректировать ширину щели таким образом, чтобы на экране возникла четкая и симметричная дифракционная картина. Произвести визуальное наблюдение дифракционной картины. Для этого перед экраном установить лист белой бумаги и, изменяя с помощью микрометра 3ширину щели в пределах 0 до 0,2 мм, наблюдать изменение дифракционной картины. Обратить внимание на то, как изменяется положение дифракционных максимумов, их яркость и ширина. Записать результаты наблюдения. Убрать лист бумаги. С помощью линейки 9 измерить расстояние L от щели до экрана, занести значение Lв таблицу. Установить на барабане микрометра ширину щели 0,12 мм, при этом действительная ширина щели будет равна: b = 0,12 мм – 0,08 мм = 0,04 мм По шкале на экране определить xлmи xпm– координаты максимумов первого (m=1), второго (m=2) и третьего (m=3) порядков, расположенных симметрично слева и справа от центрального максимума нулевого порядка. Результаты занести в таблицу. Установив ширину щели 0,08 мм, провести измерения в соответствии с п.6. Повторить измерения с шириной щели 0,12 мм и 0,16 мм. По формуле (10) вычислить экспериментальные значения углов дифракции φэксп. По формуле (9) рассчитать теоретические значения этих углов φтеор. Результаты вычислений занести в таблицу. Таблица
φПрак, (рад) Для b=0.04 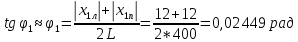 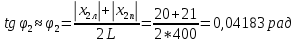 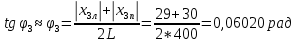 Для b=0.08 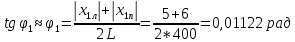 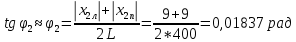 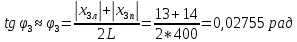 Для b=0.12 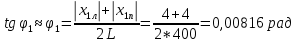 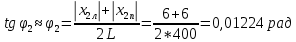 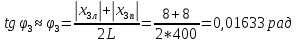 Для b=0.16 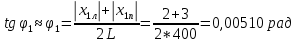 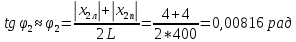 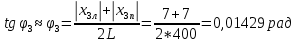 φтеор, (рад) 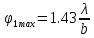; ; 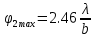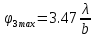Приведем пример расчетов для b=0.04 далее по аналогии: 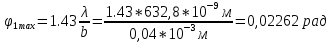 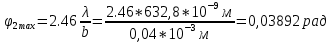 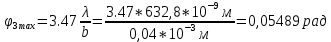 Сравнить между собой значения экспериментальных и теоретических углов дифракции. В выводах отразить результаты этого сравнения.
Среднеарифиметическая погрешность : 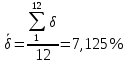 Вывод: В ходе выполнения работы, я произвел наблюдение на экране картины дифракции плоской световой волны на щели, изучил влияние ширины щели на расположение дифракционных максимумов и экспериментально определил углы дифракции, соответствующих максимумам интенсивности света на экране, и сравнение их с теоретическими углами дифракции отклонение между которыми составило 7,125% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
