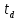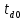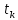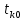лаба 3 механика лэти. господибожеспасиипомогиуже4утрагосподипожалуйста. Исследование динамики колебательного и вращательного движения
 Скачать 240.17 Kb. Скачать 240.17 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ЭТПТ отчет по лабораторной работе №3 по дисциплине «Физика» Тема: Исследование динамики колебательного и вращательного движения
Санкт-Петербург 2022 Цель работы. Исследование динамики колебательного движения на примере крутильного маятника, определение момента инерции маятника, модуля сдвига материала его подвеса и характеристик колебательной системы с затуханием (логарифмического декремента затухания и добротности колебательной системы). Основные теоретические положения. Приборы и принадлежности: крутильный маятник, секундомер. Применяемый в работе крутильный маятник (рис. 1) представляет собой диск 1, закрепленный на упругой стальной проволоке 2, свободный конец которой зажат в неподвижном кронштейне 3. На кронштейне расположено кольцо 4, масса которого известна. Кольцо 4 можно положить сверху на диск 1, изменив тем самым момент инерции маятника. Для отсчета значений угла поворота маятника служит градуированная шкала 5, помещенная на панели прибора снизу от диска 1.  Рисунок 1  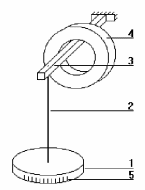 Исследуемые закономерности: Момент инерции крутильного маятника Момент инерции (аналог инертной массы тела при его поступательном движении) – физическая величина, характеризующая инертные свойства твердого тела при его вращении. В соответствии с одной из формулировок основного уравнения динамики вращательного движения M I ε где момент инерции I связывает угловое ускорение тела и момент сил M, действующих на него. Если твердое тело вращается вокруг неподвижной оси, то момент инерции относительно этой оси вычисляется как сумма произведений элементарных масс Δmi, составляющих тело, на квадраты их расстояний ri до оси вращения, т.е. 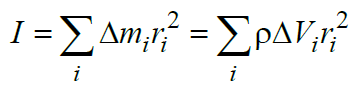 где ρ – плотность тела, ΔVi – элементы объема. Таким образом, момент инерции является аддитивной величиной. В случае сплошного тела сумма в определении момента инерции пере- ходит в интеграл: 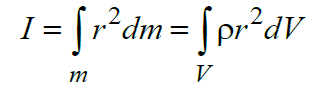 Крутильный маятник совершает вращательное колебательное движение вокруг оси, совпадающей с направлением стальной проволоки. Используя основное уравнение динамики вращательного движения, можно определить момент инерции маятника, а также физические величины, описывающие вращательное движение. Уравнение движения крутильного маятника При повороте тела, закрепленного на упругом подвесе, в результате деформации сдвига возникает вращающий момент упругих сил M = -kφ, где k – коэффициент кручения, зависящий от упругих свойств материала подвеса, его размеров и формы, φ - угол поворота диска маятника. Без учета сил трения в подвесе уравнение движения тела имеет вид 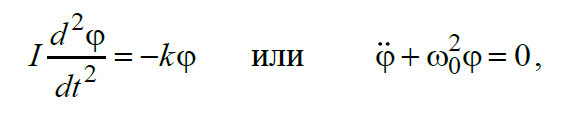 которое является уравнением гармонического осциллятора с частотой собственных колебаний 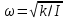 , I– момент инерции диска крутильного маятника. , I– момент инерции диска крутильного маятника.Трение в подвесе создает тормозящий момент, пропорциональный скорости движения маятника, 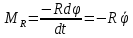 , где R – коэффициент со- противления. С учетом сил трения уравнение движения маятника принимает вид: , где R – коэффициент со- противления. С учетом сил трения уравнение движения маятника принимает вид: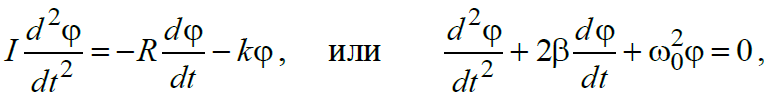 в котором коэффициент β = R/2I называют коэффициентом затухания. Последнее уравнение является уравнением гармонического осциллятора с затуханием. Решение этого уравнения при 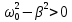 описывает затухающие колебания маятника и имеет вид (при условии, что диск повернут относительно положения равновесия и отпущен без толчка) описывает затухающие колебания маятника и имеет вид (при условии, что диск повернут относительно положения равновесия и отпущен без толчка) 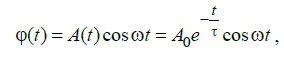 (1) (1) где 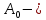 начальная амплитуда колебаний маятника, измеряемая в радианах, начальная амплитуда колебаний маятника, измеряемая в радианах, 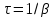 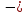 время затухания колебаний, определяющее скорость убывания амплитуды A(t) колебаний маятника, численно равное времени, за которое амплитуда колебаний убывает в е раз время затухания колебаний, определяющее скорость убывания амплитуды A(t) колебаний маятника, численно равное времени, за которое амплитуда колебаний убывает в е раз 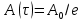 (рисунок 2) (рисунок 2)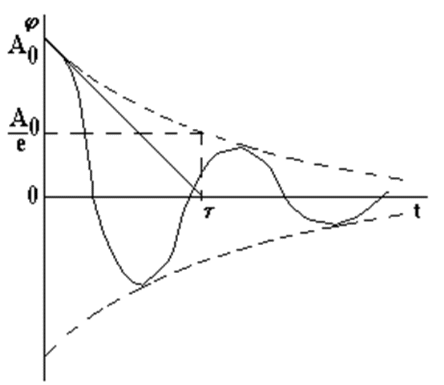 Рисунок 2 ω – частота колебаний осциллятора с затуханием, связанная с собственной частотой соотношением 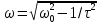 . Время затухания колебаний τ выражается через момент инерции I и коэффициент сопротивления R материала подвеса маятника . Время затухания колебаний τ выражается через момент инерции I и коэффициент сопротивления R материала подвеса маятника 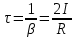 . .Исследуемый в работе крутильный маятник представляет собой сложную систему (диск с различными креплениями, прикрепленный к проволочному подвесу) с неизвестным моментом инерции 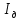 , который представляет собой постоянную часть исследуемой системы. Если на диск маятника положить тело с известным моментом инерции кольцо с моментом инерции , который представляет собой постоянную часть исследуемой системы. Если на диск маятника положить тело с известным моментом инерции кольцо с моментом инерции 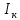 , то момент инерции маятника станет равным , то момент инерции маятника станет равным 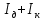 . Коэффициент кручения подвеса маятника при этом не изменяется: . Коэффициент кручения подвеса маятника при этом не изменяется: 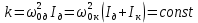 , где , где 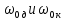 собственные частоты крутильных колебаний «диска» маятника без кольца и с кольцом. Отсюда можно найти неизвестный момент инерции диска маятника собственные частоты крутильных колебаний «диска» маятника без кольца и с кольцом. Отсюда можно найти неизвестный момент инерции диска маятника 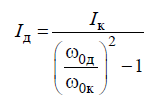 (2) (2)где 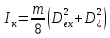 – момент инерции кольца, – момент инерции кольца, 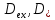 – внешний и внутренний диаметры кольца, m – его масса. – внешний и внутренний диаметры кольца, m – его масса. Крутильный маятник как диссипативная система Полная энергия колебаний маятника убывает со временем по закону 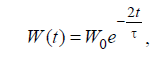 (3) (3)где  – начальная энергия колебаний. Убывание энергии происходит за счет совершения работы против сил трения. Энергия при этом превращается в тепло. Скорость диссипации энергии (мощность потерь) может быть найдена как: – начальная энергия колебаний. Убывание энергии происходит за счет совершения работы против сил трения. Энергия при этом превращается в тепло. Скорость диссипации энергии (мощность потерь) может быть найдена как: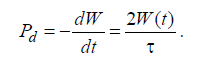 (4) (4)Помимо коэффициента затухания β (или времени затухания τ) и мощности потерь 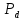 колебательная диссипативная система характеризуется также добротностью Q, позволяющей судить о способности системы сохранять энергию. Добротность определяется отношением запасенной системой энергии к потерям энергии за время колебательная диссипативная система характеризуется также добротностью Q, позволяющей судить о способности системы сохранять энергию. Добротность определяется отношением запасенной системой энергии к потерям энергии за время 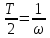 , что соответствует изменению фазы колебания на 1 радиан. Из этого определения следует, что , что соответствует изменению фазы колебания на 1 радиан. Из этого определения следует, что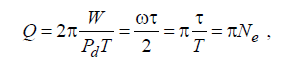 (5) (5)т.е. добротность численно равна числу колебаний за время 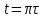 . За это время амплитуда колебаний уменьшается в . За это время амплитуда колебаний уменьшается в 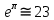 раза, а энергия колебаний в раза, а энергия колебаний в 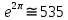 раз, иными словами за это время колебания практически затухают. Часто также используется параметр раз, иными словами за это время колебания практически затухают. Часто также используется параметр 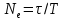 – число колебаний, за которое амплитуда колебаний уменьшается в e раз. – число колебаний, за которое амплитуда колебаний уменьшается в e раз.В технике для характеристики колебательных систем с затуханием вводят декремент затухания Δ, равный отношению амплитуд колебаний, отличающихся на период колебаний, и его логарифм – логарифмический декре- мент затухания 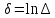 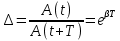 , откуда , откуда 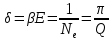 Определение модуля сдвига Методом крутильных колебаний пользуются для косвенного измерения модуля сдвига G материала подвеса. Модуль сдвига характеризует упругие свойства материала и в случае малых деформаций равен силе, действующей на единицу площади S при единичном угле сдвига γ (рис. 3) касательно сдвигу слоев вещества в месте определения модуля G. 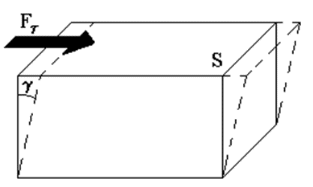 Рисунок 3 Для подвеса из стальной проволоки модуль сдвига определяется из со- отношения 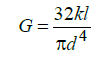 (6) (6)Где l – длина подвеса, d – его диаметр, k – его коэффициент кручения. Модуль сдвига G связан с модулем Юнга, характеризующим сопротивление материала сжатию или растяжению, соотношением 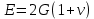 . Коэффициент Пуассона . Коэффициент Пуассона 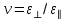 – отношение поперечной и продольной относительной деформации образца материала и для металлов близок к 0.3 – отношение поперечной и продольной относительной деформации образца материала и для металлов близок к 0.3Обработка результатов эксперимента. Задание по обработке результатов 1.
Ранжируем выборку
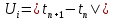 , , 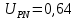 при P=95%, N=5 при P=95%, N=5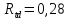 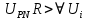 ,промахов нет ,промахов нет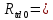 3,91 3,91 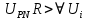 ,промахов нет ,промахов нет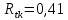 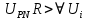 ,промахов нет ,промахов нет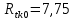 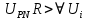 ,промахов нет ,промахов нетРассчитываем среднее значение 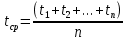 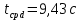 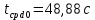 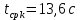 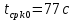 Рассчитываем СКО по формуле 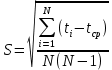 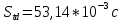 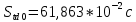 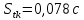 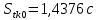 Рассчитаем случайную погрешность по формуле 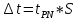 , где , где 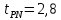 , при P=95%, N=5. , при P=95%, N=5.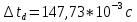 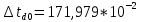 c c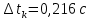 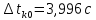 Найдём полную погрешность измерений 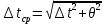 (прим. θ=0,01 c) (прим. θ=0,01 c)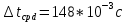 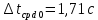 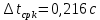 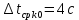 Запишем результаты в стандартной форме 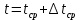 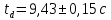 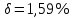 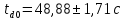 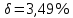 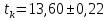 c c 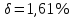 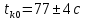 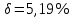 2. Вычислим периоды( 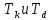 ) пользуясь методом переноса погрешностей ) пользуясь методом переноса погрешностейРассчитаем среднее значение функции 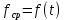 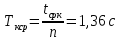 Вычисляем частные производные 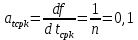 Полная погрешность функции 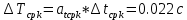 Результат измерения 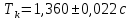 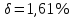 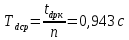 Частные производные 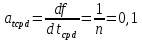 Полная погрешность 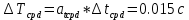 Результат измерения 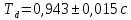 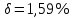 3. Определим время затухания маятника методом переноса погрешностей Предположим, что установка хорошо настроена. Тогда 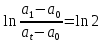 Рассчитываем значение функции 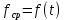 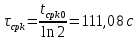 Вычисляем частные производные 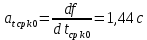 Вычисляем полную погрешность 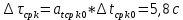 Результат измерения 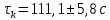 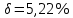 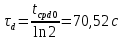 Частные производные 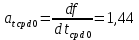 Полная погрешность 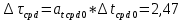 Результат измерения 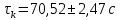 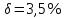 4. Рассчитаем значение функции 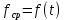 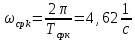 Вычисляем частные производные 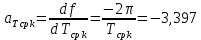 Вычисляем полную погрешность 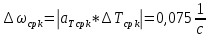 Результат измерения 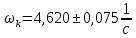 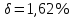 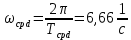 Частные производные 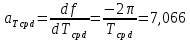 Полная погрешность 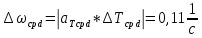 Результат измерения 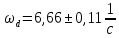 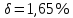 Определим собственные частоты Рассчитываем значение функции 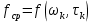 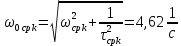 Вычисляем частные производные 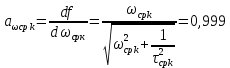 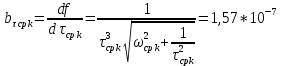 Вычислим полную погрешность 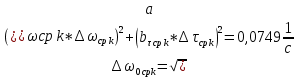 Результат измерения 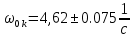 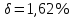 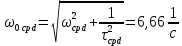 Вычисляем частные производные 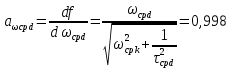 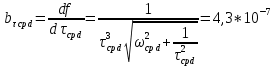 Вычислим полную погрешность 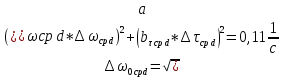 Результат измерений 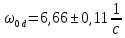 5. 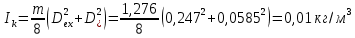 6. Рассчитаем значение функции 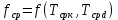 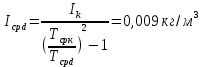 Найдём частные производные 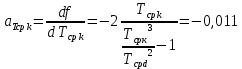 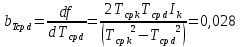 Вычислим полную погрешность 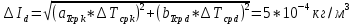 Результат измерений 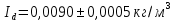 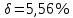 7. Вычислим значение 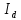 через плотность через плотность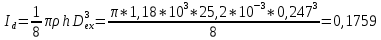 Полученное значение момента инерции для диска больше экспериментального т.к. числа малы, а мы не учитываем всех погрешностей 8. Рассчитаем значение функции 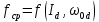 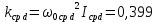 Найдём частные производные 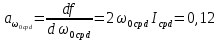 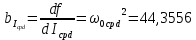 Вычислим полную погрешность 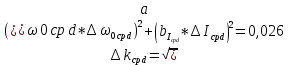 Результат измерений 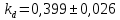 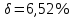 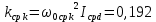 Найдём частные производные 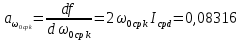 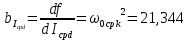 Вычислим полную погрешность 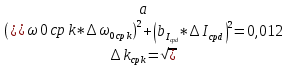 Результат измерений 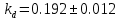 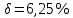 Модуль сдвига 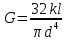 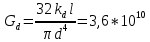 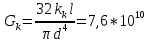 Модуль Юнга 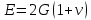 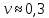 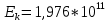 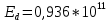 9. 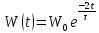 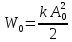 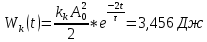 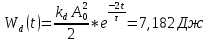 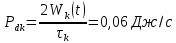 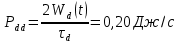 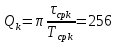 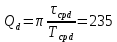 10.  Т.к. необходимо построить график для маятника без кольца уравнение примет вид  График  Уравнение амплитуды, в свою очередь, примет вид 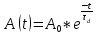 График 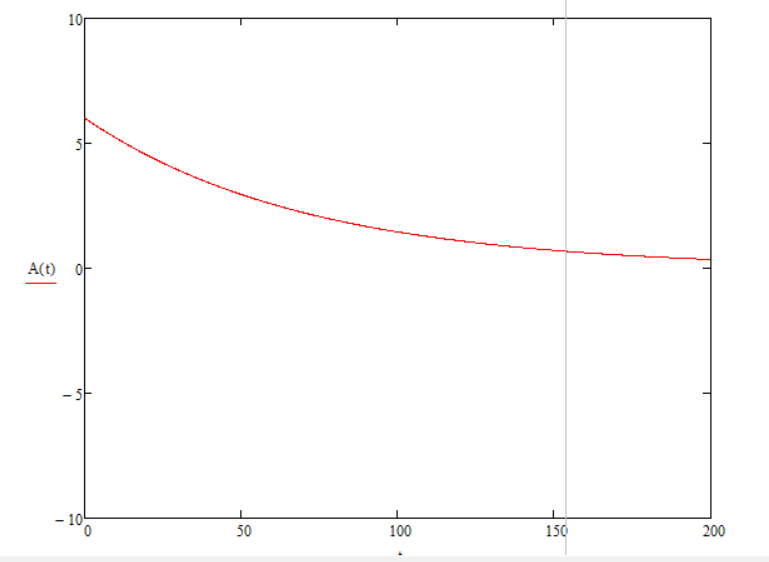 Выводы. Выполнив данную работу, я провёл исследование динамики колебательного движения крутильного маятника. Во время исследования, путём экспериментов, были получены данные(время десяти колебаний с кольцом\без кольца; время, за которое амплитуда колебаний уменьшилась вдвое), на основании которых были рассчитаны различные характеристики колебательного движения(период колебаний с кольцом\без кольца; время затухания маятника; собственная частота колебаний маятника; коэфф. кручения). Помимо этого были получены некоторые другие данные(модуль сдвига материала подвеса; полная энергия, мощность потерь и добротность маятника). В процессе выполнения работы обнаружилось, что система обладает хорошей способностью сохранять энергию, т.к. она имеет высокую добротность и достаточно малыми потерями энергии. Протокол |