Лабораторное работа Максвелаа. лабораторная работа 5. Лабораторная работа 5 Определение логарифмического декремента затухания с помощью маятника Максвелла
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Лабораторная работа №5 Определение логарифмического декремента затухания с помощью маятника Максвелла Цель работы: изучение затухающих колебаний и метода расчета логарифмического декремента затухания.
Вывод: В результате выполненной лабораторной работы было выявлено θср =0,12 также вычислено затухающее колебание методом расчета логарифмического декремента затухание, процессе работы определено что Δθср = 0,03 относительная погрешность 25%. Контрольные вопросы 1. Какие колебаниями называются гармоническими? Гармонические колебания — это такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса. 2. Что называется периодом колебания? Период колебаний— наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние, в котором она находилась в первоначальный момент, выбранный произвольно). 3. Запишите формулу, связывающую период и частоту колебаний. Формула периода колебаний T = t/N T — период [с] t — время [с] N — количество колебаний [—] Формула частоты ν = N/t = 1/T ν — частота [Гц] t — время [с] T — период [с] N — количество колебаний [—] 4. Какие колебаниями называются затухающими? Затухающие колебания– это колебания, которые происходят в незамкнутой системе, то есть колебания, которые происходят в том числе под действием силы трения. Амплитуда таких колебаний постепенно затухает. 5. Являются ли затухающие колебания гармоническими? Затухающие колебания возникают при наличии сил сопротивления, поэтому не являются гармоническими. 6. Запишите формулу для амплитуды затухающих колебаний. Амплитуды А затухающих колебаний от времени t: A = A₀e-βt,где A₀ – начальная амплитуда; β – коэффициент затуханий. 7. Что называется логарифмическим декрементом затухания? От чего он зависит? Логарифмический декремент колебаний (декремент затухания; от лат. decrementum — «уменьшение, убыль») — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины. 8. Как записать закон механической энергии для маятника Максвелла? 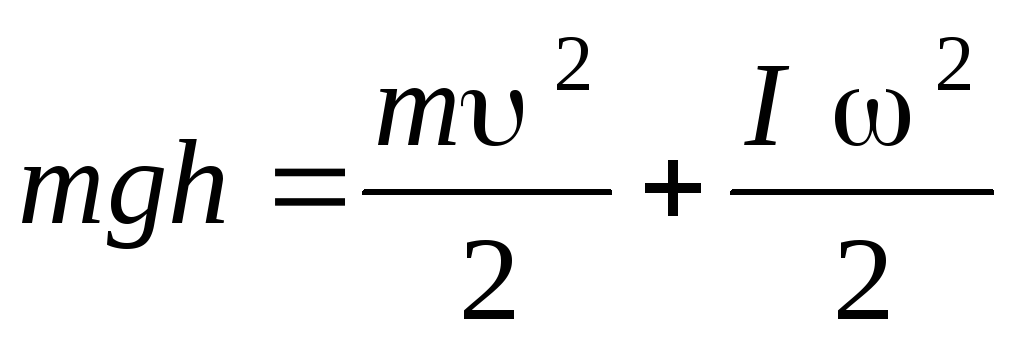 Механическая энергия маятника Максвелла представляет собой сумму кинетической и потенциальной энергий. Если принять за начало отсчета потенциальной энергии положение маятника в верхней точке, то по мере его опускания потенциальная энергия становится отрицательной. 9. Выведите рабочую формулу для определения логарифмического декремента затухания. Логарифмический декремент затухания будет равен его произведению на период колебаний: λ = β T λ = β T.  |
