Фин. мат-ка _8. Решение, где i процентная ставка s будущая сумма 50 p первоначальный капитал 35

• Название: Решение, где i процентная ставка s будущая сумма 50 p первоначальный капитал 35
• Дата: 11.04.2023
• Размер: 71.12 Kb.
• Имя файла: Фин. мат-ка _8.docx
• Тип: Решение; #1055190

Вариант 8

Задание 1: Определите простую процентную ставку, при которой первоначальный капитал 35 тыс.у.е. достигнет 50 тыс.у.е. через 120 дней. Проценты точные.

Решени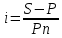е:

, где:

i - процентная ставка;

S - будущая сумма - 50;

P - первоначальный капитал - 35;

n - количество периодов продолжительности финансовой операции – 120/365.

i= 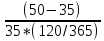=1,30 или 130%

Задание 2:Банк за 20 дней до срока погашения учел вексель на сумму 40 тыс. руб. Доход банка составил 800 руб. Какую простую учетную ставку использовал банк, если считать в году 360 дней?

Решени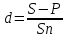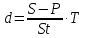е:

, где

P  вложенная сумма (сумма, которую получает владелец векселя при его учете);

S – наращенная сумма (номинальная стоимость векселя);

N  количество периодов продолжительности финансовой операции;

d  простая учетная ставка;

t  продолжительность финансовой операции в днях;

T  количество дней в году;

D  дисконт.

(360·800) / (40000 · 20) = 0,36 или 36% - простая учетная ставка банка.
Задание 3: Рассчитать накопленную сумму, если на вклад в 2 млн. руб. в течение 5 лет начисляются непрерывные проценты с силой роста 10%.

Решение:

S = Pe^n ,где:

S – наращенная сумма;

P – вложенная сумма;

n – количество лет.

2000000 • е^0,1*5 = 2000000*1,64872 = 3 297 440 руб. – накопленная сумма через 5 лет.
Задание 4: В банк 12 июля предъявлен для учета вексель на сумму 280 тыс. руб. со сроком погашения 15 октября того же года. Банк учитывает вексель по сложной учетной ставке 22% годовых, считая год равным 360 дней и проводя приблизительный подсчет дней. Определить сумму, которую получит векселедержатель, и доход банка.

Решени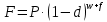е:

, где

F – наращенная сумма;

P – вложенная сумма;

n – количество лет;

d – сложная учетная ставка;

m – количество начислений процентов в году;

w – целая часть периода финансовой операции;

f – дробная часть периода финансовой операции.

F=280000*(1-0,22)^95/360=262230,30 руб. - получит векселедержатель.

D= S – P

D= 280000-263136,86=17769,7 руб. - доход банка.

Задание 5: Номинальная процентная ставка, компенсирующая при наращении инфляцию, составляет 48% годовых. Определите инфляцию за квартал, если начисление сложных процентов осуществляется каждый месяц.

Решение:

Приравняем годовой индекс инфляции к множителю наращения за год

i¹²= 0,48, получаем:

I_рⁱ= (1 +i¹²/12)¹²= (1 + 0,48/12)¹²= 1,60103

Поэтому индекс инфляции за квартал (0,25 года) составит:

I_р^0,25= 1,1249 (корень 4-ой степени из 1,60103) или 12,49%
Задание 6:Инвестор владеет тремя видами акций. Он произвел оценку следующего совместного вероятностного распределения доходностей: 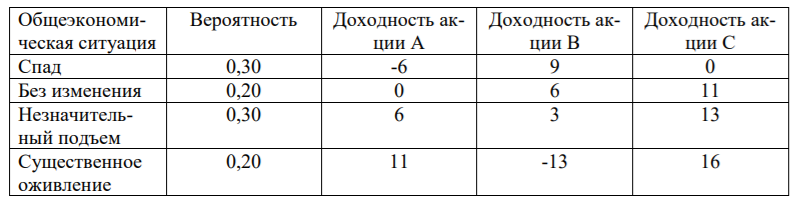Определите: а) среднюю доходность по акциям А, В, С, б) дисперсию доходности для этих бумаг, в) ожидаемую доходность и стандартное отклонение портфеля, если инвестор вкладывает 45% средств в акции А, 25% - в акции В, 30% - в акции С. Предполагается, что доходность каждой ценной бумаги является некоррелированной с доходностью остальных ценных бумаг.

Решение:

а) Вычислим среднюю доходность акций каждого вида по формуле: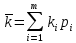



где ki – доходность в данной общеэкономической ситуации, pi – вероятность данной общеэкономической ситуации, m – число различных экономических ситуаций.

Средняя доходность акций А равна 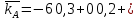у е

Средняя доходность акций В равна = 2,2 у е

Средняя доходность акций С равна = 9,3 у е

б) Найдем дисперсию доходности акций каждого вида по формуле: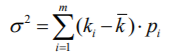



Дисперсия доходности акций А: (-6-2,2)²*0,3+(0-2,2)²*0,2+(6-2,2)²*0,3+(11-2,2)²*0,2=20,172+0,968+4,332+15,488=40,96

Дисперсия доходности акций В: (9-2,2)²*0,3+(6-2,2)²*0,2+(3-2,2)²*0,3+(-13-2,2)²*0,2= 13,872+2,888 +0,192+46,208=63,16

Дисперсия доходности акций С: (0-9,3)²*0,3+(11-9,3)²*0,2+(13-9,3)²*0,3+(16-9,3)²*0,2=25,947+0,578+4,107+8,978=39,61

в) Рассчитаем ожидаемую доходность портфеля Р при условии, что доля бумаг каждого вида в этом портфеле:

XА = 0,45, XВ = 0,25, XС = 0,3.

Средняя ожидаемая доходность портфеля равна:

2,2*0,45+2,2*0,25+9,3*0,3=0,99+0,55+2,79=4,33

Стандартное отклонение доходности портфеля из трех видов ценных бумаг А, В и С:

√40,96*0,2025+63,16*0,0625+39,61*0,09=√8,2944+3,9475+3,5649=√20,15=4,49