2 лаба МЭТ. 2 лаба мэт. Исследование электрических свойств полупроводниковых материалов

Название	Исследование электрических свойств полупроводниковых материалов
Анкор	2 лаба МЭТ
Дата	11.11.2020
Размер	63.68 Kb.
Формат файла
Имя файла	2 лаба мэт.docx
Тип	Исследование #149748

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра микро- и наноэлектроники

ОТЧЕТ

по лабораторной работе №2

по дисциплине «Материалы электронной техники»

Тема: Исследование электрических свойств полупроводниковых материалов

Студент гр. 8283 Преподаватель

Орехов А.В. Лазарева Н.П.

Санкт-Петербург 2019

Цель работы

Сравнить температурные зависимости сопротивления полупроводников с различной шириной запрещенной зоны; определить ширину запрещенной зоны и энергию ионизации легирующих примесей в материалах.

Основные понятия и определения

Полупроводники – материалы с электронной электропроводностью, которые по своему удельному сопротивлению занимают промежуточное положение между проводниками и диэлектриками. Условный диапазон удельных сопротивлений полупроводников ограничивают значениями 10^-5-10⁸Ом∙м.

Характерной особенностью полупроводниковых материалов является сильно выраженная зависимость удельной проводимости от внешних энергетических воздействий, а также от концентрации и типа примесей.

В зависимости от степени чистоты полупроводники подразделяются на собственные и примесные.

Собственный – это такой полупроводник, в котором можно пренебречь влиянием примесей при данной температуре. Содержание примесей в них не превышает 10^-9…10^-8%, и существенного влияния на удельную проводимость полупроводника они не оказывают.

Примесный – это такой полупроводник, электрофизические свойства которого в основном определяются примесями.

При T = 0 К в полупроводниковых кристаллах нет ни одного квазисвободного носителя заряда, способного принять участие в направленном движении при воздействии внешнего фактора, т. е. при температуре абсолютного нуля полупроводник не обладает электропроводностью. Прочность ковалентной

(ионно-ковалентной) связи (энергия связи) соответствует ширине запрещенной зоны полупроводника ΔЭ.

При температурах, отличных от 0 K, часть носителей заряда, обладая средней тепловой энергией E_ср kT, способна разорвать химическую связь, что приводит к образованию равного количества электронов в зоне проводимости n_i и дырок в валентной зоне p_i. Процесс термогенерации носителей заряда носит вероятностный характер, и в случае генерации собственных носителей заряда их концентрации определяются соотношением:
n_i=p_i exp()
Чтобы управлять значением проводимости и типом электропроводности полупроводника, в узлы решетки вводят легирующие примеси, валентность которых отличается на ±1 от валентности собственных атомов (водородоподобные доноры или акцепторы). Такие примеси создают в запрещенной зоне полупроводника дополнительные уровни вблизи краев соответствующих зон: доноры – вблизи дна зоны проводимости, акцепторные – вблизи потолка валентной зоны. Энергия термогенерации носителей заряда, обусловленных введением примесей ∆Эпр, в 50…100 раз меньше ширины запрещенной зоны ∆Э, так что при температурах работы полупроводниковых приборов ( 300 K) именно примеси определяют суммарную концентрацию носителей заряда в полупроводнике. Очевидно, что концентрация носителей заряда при введении в полупроводник примесей n_пр определяется процессом термогенерации носителей заряда:
n_пр exp(-∆Э_пр/(2kT))
Чтобы не нарушить совершенства кристаллической структуры полупроводника, легирующие примеси вводят в концентрациях, много меньших (на несколько порядков), чем концентрация собственных атомов N_пр << N_соб, но и

такого количества примесей достаточно, чтобы управлять и типом, и значением проводимости полупроводника.
Суммарная концентрация носителей заряда в полупроводнике определяется как собственными носителями заряда n_i, так и концентрацией ионизированных примесей n_пр:
n ≈ n_i + n_пр

Рис. 1 - температурные зависимости проводимости в полупроводниках, содержащих различные концентрации примесей: 1 – N_пр1; 2 – N_пр2; N_пр2 > N_пр1

Обработка результатов

Расчёт удельного сопротивления исследуемых полупроводниковых материалов для каждой температурной точки по формуле

𝑆

𝜌 = 𝑅 _𝐿

где R- сопротивление образца; S- площадь поперечного сечения образца; L- длина образца.

Таблица 1.

	Si	Ge	SiC	InSb
S, м²	2,0E-07	2,0E-07	1,2E-06	1,0E-07
L, м	0,03	0,03	0,01	0,02

Вычислим соответствующие удельные проводимости образцов по формуле: γ = 1/ρ

Пример вычислений (Si) для T=303K:

ρ = R*S/L =

γ = 1/ρ =

ln(γ) =
Таблица 2, Si.

Т, К	T ˉ¹, Kˉ¹	R, Ом	ρ, Ом*м	γэкс, См/м	ln γ
298	0,0034	991,4	6,61E-03	1,51E+02	5,019272
303	0,0033	1024	0,00683	146,48438	4,986919
307	0,0033	1050	0,007	142,89797	4,962131
310	0,0032	1074	0,00716	139,61281	4,938873
313	0,0032	1107	0,00738	135,46464	4,908711
319	0,0031	1157	0,00771	129,63443	4,864718
329	0,003	1245	0,0083	120,53033	4,791901
340	0,0029	1326	0,00884	113,1307	4,728544
368	0,0027	1592	0,01061	94,221106	4,545644
382	0,0026	1703	0,01135	88,085031	4,478303
420	0,0024	2421	0,01614	61,957869	4,126455

Таблица 3, Ge.

Т, К	T ˉ¹, Kˉ¹	R, Ом	ρ, Ом*м	γэкс, См/м	ln γ
298	0,0034	290	0,00193	517,24138	6,24851
303	0,0033	294,8	0,00197	508,81954	6,232093
307	0,0033	298,3	0,00199	502,84948	6,220291
310	0,0032	301,6	0,00201	497,34748	6,209289
313	0,0032	305,8	0,00204	490,51668	6,195459
319	0,0031	311,1	0,00207	482,16008	6,178276
329	0,003	316,7	0,00211	473,63435	6,160436
340	0,0029	315,1	0,0021	476,03935	6,165501
368	0,0027	247,7	0,00165	605,57126	6,406172
382	0,0026	205,3	0,00137	730,63809	6,593918
420	0,0024	71,8	0,00048	2089,1365	7,644506

Таблица 4, SiC.

Т, К	T ˉ¹, Kˉ¹	R, Ом	ρ, Ом*м	γэкс, См/м	ln γ
298	0,0034	7280	8,74E-01	1,1446886	0,135133
303	0,0033	6580	7,90E-01	1,266464	0,236229
307	0,0033	6108	7,33E-01	1,3643309	0,310664
310	0,0032	5691	6,83E-01	1,4643004	0,381378
313	0,0032	5197	6,24E-01	1,6034892	0,472182
319	0,0031	4579	5,49E-01	1,8199025	0,598783
329	0,003	3716	4,46E-01	2,2425547	0,807616
340	0,0029	3104	3,72E-01	2,6847079	0,987572
368	0,0027	1930	2,32E-01	4,3177893	1,462744
382	0,0026	1499	1,80E-01	5,5592617	1,715465
420	0,0024	686,3	8,24E-02	12,142406	2,496704

Таблица 5, InSb.

Т, К	T ˉ¹, Kˉ¹	R, Ом	ρ, Ом*м	γэкс, См/м	ln γ
298	0,0034	32	1,60E-04	6250	8,740337
303	0,0033	31	1,55E-04	6451,6129	8,772085
307	0,0033	29,93	1,50E-04	6682,2586	8,807211
310	0,0032	29,11	1,46E-04	6870,4912	8,834991
313	0,0032	28,01	1,40E-04	7140,307	8,873511
319	0,0031	26,31	1,32E-04	7601,6724	8,936124
329	0,003	23,61	1,18E-04	8470,9869	9,044402
340	0,0029	21,43	1,07E-04	9332,7112	9,141281
368	0,0027	16,04	8,02E-05	12468,828	9,430987
382	0,0026	14,57	7,29E-05	13726,836	9,527108
420	0,0024	9,82	4,91E-05	20366,599	9,921652

Построение температурные зависимости удельной электрической проводимости полупроводников по данным таблиц 2-5, откладывая по оси абсцисс параметр T^-1, а по оси ординат – значения ln(γ).

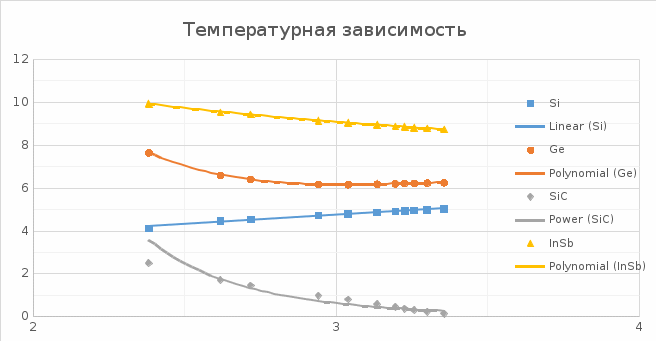
Рис. 2 – график температурной зависимости удельной электрической проводимости полупроводников.

Расчет концентрации собственных носителей заряда в полупроводниках Si, Ge, InSb и SiC при T = 300 К по формуле:

Таблица 6.

	ΔЭ, эВ	μn,	μp	Nc	Nv	T
Si	1,12	0,13	0,05	2,74E+25	1,05E+25	300
Ge	0,66	0,39	0,19	1,02E+25	6,1E+24
InSb	0,18	7,8	0,075	3,7E+22	6,3E+24
SiC	2,9	0,04	0,006	1,44E+25	1,93E+25

Пример вычислений (Si):

Таблица 7.

Проводник	ni
Si	6,68028E+15
Ge	2,26425E+19
InSb	1,48698E+22
SiC	7,422801334

Оценка значения собственной электропроводности в этих полупроводниках при 300 К:

_i qn__n  _p_

Пример вычислений для SiC:

__i qn__n  _p__
Таблица 8.

Проводник	yi
Si	2,03E-04
Ge	2,22E+00
InSb	1,98E+04
SiC	5,77E-20

Сравнение полученных в результате расчетов значения ^_i с экспериментальными данными ^γэксп, определение проводимости исследуемых образцов в интервале температур от Т_min=298 K до T_max=420 К:

а) Si:

^γэксп = 151 См/м; ^_i= 2,03 ∗ 10⁻⁴ См/м

Так как ^γэксп >> γi, значит в полупроводнике при T=298 К наблюдается только примесная проводимость. Следует оценить, все ли примеси ионизированы в исследованном температурном интервале или нет. Для этого сравним энергию ионизации примеси ΔЭпр с энергией тепловой генерации kT_max.

kT_max =

ΔЭпр :

ΔЭпр ≈ kT_max
б) Ge:

^γэксп = 517 См/м; ^_i= 2,2 См/м

^γэксп >> γi

В Ge при T = 298 К наблюдается примесная проводимость.

kT_max =

ΔЭпр =

ΔЭпр < kT_max

При Т = 328 К начинается участок собственной электропроводности германия.

Определим по углу наклона кривой ширину запрещенной зоны:

в) SiC:

^γэксп =1,14 См/м; ^_i=5,77 ∗ 10⁻²⁰ См/м

^γэксп >> ^_i

В карбиде кремния при T=298 К наблюдается примесная проводимость.

kT_max =

ΔЭпр :

ΔЭпр > kT_max

На интервале температур от Т=298 К до Т=420 К наблюдается участок ионизации примеси.

Вычислим энергию ионизации примеси:

г) InSb:

^γэксп = 6250 См/м; ^_i=19800 См/м

^γэксп ≈ γi

У антимонида индия на интервале температур от T = 298 К до Т=420 К наблюдается участок собственной электропроводности.
Найдем собственную энергию ионизации:

Рассчитаем n_i _эксппри T = 298 К

Пример вычислений:

Таблица 9.

Проводник	niэкс
Si	4,62E+22
Ge	5,35E+21
InSb	2,58E+21
SiC	1,87E+20

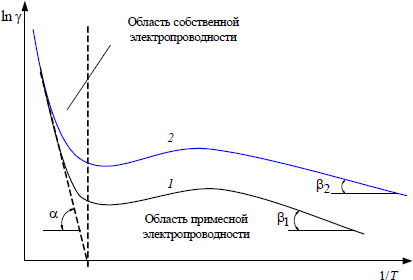
Вывод.

В ходе выполнения данной лабораторной работы, при получении экспериментальных температурных зависимостей сопротивлений полупроводников с различной шириной запрещенной зоны, были получены следующие выводы:

У Si-кремния наблюдается участок истощения примеси, что можно хорошо увидеть на графике (уменьшение удельной проводимости с ростом температуры), это не позволяет определить ни энергию активации примеси, ни ширину запрещенной зоны полупроводника;

У Ge-германия наблюдается переход с участка истощения примеси в зону собственной электропроводности, т.е. уменьшение удельной проводимости до минимального значения при температуре 329 К, а после, резкого увеличения. Экспериментально установленная ширина запрещенной зоны германия ΔЭ_Ge=

У SiC наблюдается участок ионизации примесей, т.е. увеличения удельной проводимости с ростом температуры, где γ_эксп >> γ_i. Экспериментально установленная энергия ионизации примесей карбида кремния ΔЭ_прSiC=

У InSb наблюдается участок собственной электропроводности, т.е. график возрастает при увеличении температуры, где γ_эксп ≈ γ_i. Ширина запрещенной зоны антимонида индия ΔЭ_InSb=