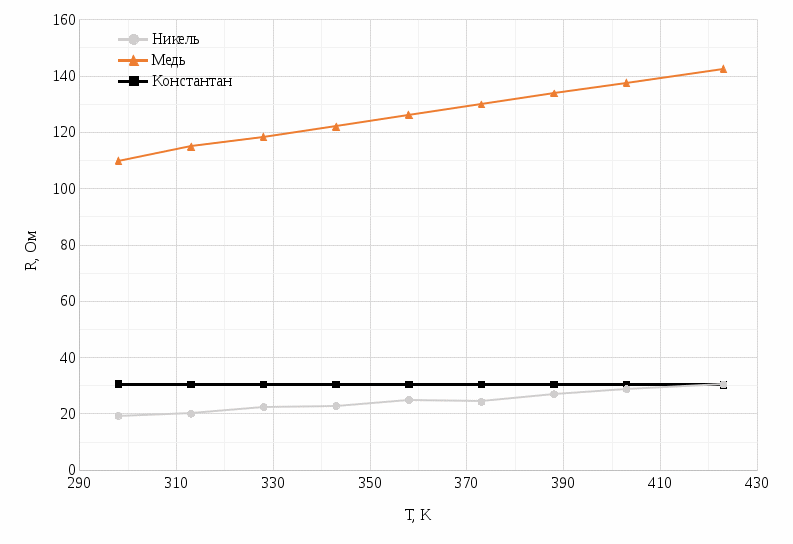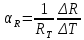МЭТ 1. МЭТ_ПРОВОДНИК. Исследование электрических свойств проводниковых материалов
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра МНЭ отчет по лабораторной работе №1 по дисциплине «МАТЕРИАЛЫ ЭЛЕКТРОННОЙ ТЕХНИКИ» Тема: ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКИХ СВОЙСТВ ПРОВОДНИКОВЫХ МАТЕРИАЛОВ
Санкт-Петербург 2023 Цели работы Измерение сопротивлений объемных и тонкопленочных резисторов; исследование зависимостей удельных электрических сопротивлений и их температурных коэффициентов от температуры и состава резистивных материалов, а также зависимостей термоЭДС термопар от разностей температур контактов. Основные понятия и определения Проводники электрического тока – это материалы и среды с малым удельным электрическим сопротивлением, значения которого находятся в пределах 10−5-10−8 Ом∙м, обладающие высокой удельной проводимостью, обусловленной наличием в них большой концентрации электрических зарядов, способных свободно перемещаться. Все металлы и сплавы на их основе в твердом и жидком состоянии и некоторые модификации углерода, механизм протекания электрического тока в которых обусловлен движением свободных электронов, относятся к проводникам электрического тока с электронной электропроводностью или проводникам первого рода. Электролиты и расплавы ионных соединений относятся к проводникам с ионной электропроводностью, или проводникам второго рода. Ионизированный газ в состоянии плазмы тоже является проводящей средой, в которой объемные плотности положительно и отрицательно заряженных частиц практически одинаковы. Высокая проводимость проводников позволяет использовать их для передачи электрической энергии, возбуждения электромагнитных полей, создания электрических межсоединений, контактирования и др. К основным электрическим характеристикам проводниковых материалов относят удельное сопротивление ρ и температурный коэффициент удельного сопротивления αρ. В процессе направленного движения электроны испытывают рассеяние на статических (атомы, вакансии, междоузельные атомы и т. д.) и динамических (тепловые колебания ионов в узлах кристаллической решетки) дефектах структуры. Интенсивность рассеяния определяет среднюю длину свободного пробега электрона и, в конечном счете, значение удельного сопротивления проводника, которое может быть рассчитано по формуле (1).
где m – масса электрона; u – средняя скорость теплового движения; e – заряд электрона; n0 – концентрация свободных электронов; λ – средняя длина свободного пробега. Электронный газ в металлах находится в вырожденном состоянии. Поэтому концентрация электронов и их средняя энергия практически не зависят от температуры, но с повышением температуры увеличивается амплитуда колебаний атомов в узлах кристаллической решетки, что приводит к более интенсивному рассеянию электронов в процессе их направленного движения. Соответственно уменьшается длина свободного пробега и возрастает удельное сопротивление. Относительное изменение удельного сопротивления при изменении температуры на один кельвин называют температурным коэффициентом удельного сопротивления, который рассчитывается по формуле (2).
В области линейной зависимости ρ(t) справедливо выражение (3).
где 0 и – удельное сопротивление и температурный коэффициент удельного сопротивления, отнесенные к температуре t0. В технике широко применяются сплавы, имеющие структуру неупорядоченных твердых растворов. Все сплавы имеют повышенное удельное сопротивление в сравнении с компонентами, входящими в их состав. Полное удельное сопротивление сплава рассчитывается по формуле (4).
где t – сопротивление, обусловленное рассеянием электронов на тепловых колебаниях узлов решетки; ост – сопротивление, связанное с рассеянием электронов на статических дефектах кристаллической структуры сплава, остающихся в металле и при температуре абсолютного нуля. Для многих двухкомпонентных сплавов значение остаточного сопротивления от состава хорошо описывается параболической зависимостью
где xA, xB – атомные доли компонентов в сплаве; С – константа, определяемая природой сплава. Температурные коэффициенты удельного сопротивления сплавов всегда значительно меньше температурных коэффициентов чистых металлов, образующих сплав. В некоторых сплавах может быть даже отрицательным. В микроэлектронике широко применяются в качестве различных элементов схем тонкие металлические пленки, получаемые методами конденсации. В очень тонких слоях такие пленки могут иметь не сплошную, а островковую структуру. Но электропроводность пленки возникает при некотором минимальном количестве осажденного металла еще до образования соединительных мостиков между островками металла. При приложении электрического поля происходит переход электронов через диэлектрические зазоры между соседними островками. Механизмами, ответственными за перенос заряда, являются термоэлектронная эмиссия и туннелирование. Сопротивление пленки островковой структуры во многом определяется и поверхностным сопротивлением диэлектрической подложки. В процессе конденсации металла на подложке происходит слияние островков и образование сначала проводящих цепочек и каналов, а затем – сплошного однородного слоя. Но и в сплошной пленке удельное сопротивление больше, чем удельное сопротивление объемного проводника, что является следствием высокой концентрации дефектов – вакансий, дислокаций, границ зерен, образующихся при срастании островков. Вследствие поверхностного рассеяния электронов и повышенной степени дефектности структуры удельное сопротивление тонких металлических пленок существенно превосходит удельное сопротивление объемного материала. Для сравнительной оценки проводящих свойств пленок пользуются таким параметром, как удельное поверхностное сопротивление
где ρ – удельное сопротивление слоя толщиной d. Параметр R□ не зависит от размера квадрата. Подбором толщины пленки можно изменять R□ независимо от удельного сопротивления. При соприкосновении двух различных металлов между ними возникает контактная разность потенциалов, которая зависит от вида контактирующих металлов и температуры. Термоэлемент, из двух различных проводников, образующих замкнутую цепь, называют термопарой. При различной температуре контактов в замкнутой цепи возникнет термоэлектрический ток. Если цепь разорвать в произвольном месте, то на концах разомкнутой цепи появится термоэлектродвижущая сила (термоЭДС). В относительно небольшом температурном интервале термоэлектродвижущая сила U пропорциональна разности температур контактов (спаев) и рассчитывается по формуле (7).
где – удельная термоэлектродвижущая сила. ТермоЭДС в контуре складывается из трех составляющих. Первая обусловлена температурной зависимостью внутренней контактной разности потенциалов Ui, которая, в свою очередь, связана с температурным изменением положения уровня Ферми. В металлах с увеличением температуры уровень Ферми смещается вниз по энергетической шкале. Поэтому на холодном конце проводника он должен располагаться выше, чем на более нагретом. Следствием смещения уровня Ферми и является возникновение контактной составляющей термоЭДС. Вторая составляющая термоЭДС, называемая объемной, обусловлена диффузией носителей заряда от горячих спаев к холодным. Средняя кинетическая энергия электронов в металле также несколько изменяется с температурой. Отсюда следует, что электроны, сосредоточенные на более горячем конце, обладают несколько большей кинетической энергией и большей скоростью теплового движения по сравнению с носителями заряда холодного конца. Поэтому они в большем количестве диффундируют от горячего конца к холодному. Диффузионный поток, перенося заряд от горячего конца к холодному, создает между ними разность потенциалов. Третья составляющая термоЭДС возникает в контуре вследствие увлечения электронов квантами тепловой энергии (фононами). Их поток также распространяется к холодному спаю («фононный ветер»). Основной вклад в термоЭДС металлических термопар вносит первая причина, т. е. разность уровней Ферми. Для точного измерения температуры используются металлические термопары с наибольшим значением термоЭДС. Точность измерения температуры обычно составляет 0,1...1,0 C, а диапазон измеряемых температур зависит от материалов термопары. Явления возникновения контактной разности потенциалов и термоЭДС следует учитывать при создании измерительных приборов и образцовых сопротивлений, где эти явления нежелательны, и, значит, следует применять металлы и сплавы с возможно меньшими значениями термоЭДС, которая может внести погрешность при измерениях. Описание установки Измерение сопротивления исследуемых проводников и термоЭДС термопар производится с помощью мультиметра, постоянно подключенного к испытательному стенду. Все исследуемые образцы расположены в корпусе стенда; резисторы R1, R2, R3 и один из спаев каждой из трех термопар помещены в общий термостат. Подключение образцов к измерительному прибору осуществляется нажатием соответствующей контактной кнопки на лицевой панели стенда. Маркировка кнопок соответствует маркировке образцов. При измерениях следует удерживать кнопку контакта к соответствующему образцу в утопленном положении. Геометрические размеры образцов указаны на лицевой панели. Ход работы Рассчитано удельное сопротивление металлических проводников, используя формулу (8) и сопротивление квадрата металлических пленок по формуле (9)
где R – сопротивление образца; S – площадь поперечного сечения; l– длина проводника.
где R – сопротивление образца; b и l – ширина и длина пленочного резистора соответственно. Пример расчета удельного сопротивления проволочного резистора из манганина: ρ= RS/ l = R (π∙(d/ 2)2) / l = 63,51∙(π∙(0,1/ 2)2)/ 1,04 = 0,480 мкОм ‧ м d, мм – диаметр проволоки Результаты остальных расчетов сведены в таблицу 1. Таблица 1 – Удельного сопротивления проволочных резисторов
Пример расчета сопротивления квадрата поверхности первого материала: R□ = Rb / l = 39,07 ‧ 2,5 / 0,2 = 488,38 Ом Результаты остальных расчетов сведены в таблицу 2. Таблица 2 – Сопротивление квадрата поверхности разных материалов
Построены температурные зависимости сопротивления R=f (T) для исследованных резисторов. Данные, использованные для построения графика находятся в таблице 4. График изображен на рисунке 1. Таблица 3 – Зависимость сопротивлений от температуры
Рассчитан температурный коэффициент удельного сопротивления металлов и сплавов по формуле (10).
где αR и αl – температурные коэффициенты сопротивления и линейного расширения соответственно. Температурные коэффициенты линейного расширения имеют следующие значения: αl никель = 12,8 ∙ 10−6 К–1; αl медь = 16,7 ∙ 10−6 К–1; αl константан = 17,0 ∙ 10−6 К–1. Температурный коэффициент сопротивления при различных температурах рассчитан по формуле (11).
где RT – сопротивление образца при данной температуре. Пример расчета температурного коэффициента удельного сопротивления никеля при температуре T = 298 K: αR= 1/RT‧(R2-RT)/(T-T2) = 1/19,27‧(20,08-19,27)/(313-298) = 2,802‧10-3 К–1 αρ = αR + αl = 2,802‧10-3 + 12,8 ∙ 10−6 = 2,815‧10-3 К–1 Таблица 4 – Температурные коэффициенты αR и αρ
Построена зависимость αρ = f (T) для исследованных материалов. Данные взяты из таблицы 4, графики изображены на рисунке 2.
Рассчитаны зависимости удельного сопротивления и температурного коэффициента удельного сопротивления от состава для сплавов системы Cu - - Ni при комнатной температуре. Удельное сопротивление рассчитано по формуле (12).
где С – постоянный коэффициент; хNi – содержание никеля в сплаве в относительных долях по массе; Первые два слагаемых в (12) характеризуют удельное сопротивление, обусловленное рассеянием электронов на тепловых колебаниях узлов кристаллической решетки. Предполагается, что эти составляющие удельного сопротивления аддитивно зависят от состава. Третье слагаемое характеризует изменение остаточного сопротивления от состава. Коэффициент С найден путем подстановки в формулу (12) значения удельного сопротивления константана и соответствующего ему содержания никеля хNi = 0,4. Подставляя различные значения xNi в формулу (12), получены точки для построения кривой ρ = f (x). Значения удельного сопротивления меди, никеля и константана взяты из справочной литературы: ρ никель = 0,068 мкОм ‧ м; ρ медь = 0,017 мкОм ‧ м; ρ константан = 0,5 мкОм ‧ м. Значения температурного коэффициента удельного сопротивления сплавов Cu-Ni при различных содержаниях никеля рассчитаны с помощью формулы (13).
где CuNi − удельное сопротивление сплава соответствующего состава, определенного по (12). Температурные коэффициенты удельного сопротивления никеля и меди взяты из таблицы 4: αρNi = 2,815‧10-3 К-1 αρCu = 3,126‧10-3 К-1 Расчет коэффициента С: С = (ρCu-Ni – ρNi ‧ xNi - ρCu (1-xNi))/ (xNi (1-xNi)) = = (0,5‧10-6-0,068‧10-6‧0,4-0,017‧10-6‧(1-0,4))/(0,4‧(1-0,4))=1,9275‧10-6 Ом‧ м Пример расчета ρCu-Ni и αρCu-Ni, при xNi= 0,2: ρCu-Ni = ρNi ‧ xNi + ρCu (1-xNi) + СxNi (1-xNi) = 0,068‧10-6‧0,2+0,017‧10-6‧(1- - 0,2)+1,9275‧10-6‧0,2‧(1-0,2) = 0,336 мкОм‧м αρCu-Ni = (ρCu (1-xNi) ‧ αρCu+ xNi‧ αρNi‧ ρNi)/ρCu-Ni = (0,017‧10-6‧(1-0,2) ‧ ‧ 3,126 ‧ 10-3+ 0,2‧ 2,815‧ 10-3‧ 0,068‧ 10-6)/ (0,336‧10-6) = 0,241 ‧10-3 К-1 Результаты остальных расчетов занесены в таблицу 5. Таблица 5 – Зависимость ρ и αρ от содержания никеля в сплаве
6. По данным таблицы 5, на рисунке 3 построены зависимости удельного сопротивления сплава ρCu–Ni и температурного коэффициента удельного сопротивления сплава αρ(хCu–Ni) от состава сплава. Также на графике отмечено экспериментально найденное значение температурного коэффициента удельного сопротивления константана (Содержание никеля в константане ≈ 40%) αρ= - 4,836‧10-6 К-1.
7. Построены температурные зависимости термоЭДС ΔU(T) для исследованных термопар по данным таблицы 6. График расположен на рисунке 4. Расчет ΔT (Tгор = 298 K): ΔT = Tгор – Tхол = 298 – 296 = 2 К Таблица 6 – Измеренное термоЭДС для различных термопар
Вывод В ходе лабораторной работы были исследованы электрические свойства проводниковых материалов. Были проведены опыты по измерению сопротивлений резисторов из различных материалов, с разными геометрическими параметрами. По эти значениям было высчитано удельное сопротивление материалов полученные результаты, и справочные значения сведены в таблице 1. Проанализировав таблицу, можно сказать, что полученные значения верны. На рисунке 1 были построен графики температурных зависимостей сопротивлений никеля, константана, и меди. Все три зависимости имеют линейный характер. При увеличении температуры росло сопротивление всех трех образцов, что соответствует теории. Это объясняется тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решетки, что приводит к увеличению частоты столкновений электронов с ними. Были рассчитаны температурные коэффициенты сопротивления, и удельного сопротивления при разных температурах. Результаты приведены в таблице 4. На рисунке 2 приведены графики зависимости температурного коэффициента удельного сопротивления. На рисунке видно, что температурный коэффициент константана близок к нулю. Константан имеют данную особенность благодаря тому, что с возрастание температуры в нём возрастает концентрация электронов. Были рассчитаны теоретические зависимости значения температурного коэффициента удельного сопротивления, и у дельного сопротивления сплава меди и никеля, от их процентного соотношения. На рисунке 3 видно, что при увеличении содержания примеси возрастает удельное сопротивление сплава. В лабораторной работе также рассматривалась зависимость термоЭДС от разницы температур различных термопар. Согласно теоретическим сведениям, зависимость должна иметь линейный характер, и угол наклона графика должен характеризоваться разницей концентраций свободных носителей зарядов в двух различных металлах. Все три графика на рисунке 4 имеют зависимость приближенную к линейной  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||