Исследование электронного парамагнитного резонанса (эпр) в слабом магнитном поле
 Скачать 3.44 Mb. Скачать 3.44 Mb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра физики  ОТЧЕТ по лабораторной работе №16 по дисциплине «Физика» ТЕМА: ИССЛЕДОВАНИЕ ЭЛЕКТРОННОГО ПАРАМАГНИТНОГО РЕЗОНАНСА (ЭПР) В СЛАБОМ МАГНИТНОМ ПОЛЕ Студент гр. 9584 Тышкевич Р.В. Преподаватель Посредник О.В.  Санкт-Петербург 2020 Лабораторная работа 16. ИССЛЕДОВАНИЕ ЭЛЕКТРОННОГО ПАРАМАГНИТНОГО РЕЗОНАНСА (ЭПР) В СЛАБОМ МАГНИТНОМ ПОЛЕ Цель работы: исследование индуцированных квантовых переходов между зеемановскими уровнями неспаренного электрона в слабом магнитном поле, определение магнитного момента атома (молекулы) и времени жизни атома в возбужденном состоянии. 107 Приборы: экспериментальная установка для возбуждения квантовых переходов между зеемановскими уровнями электронов – упрощенный спектрометр электронного парамагнитного резонанса (см. рис. 16.1). К магнитному резонансу (МР) относят совокупность явлений, которые могут наблюдаться в системе частиц (ядра, электроны, атомы, молекулы и др.), обладающих моментом импульса и магнитным дипольным моментом. Одним из частных проявлений эффекта МР служит избирательное поглощение системой магнитных диполей энергии внешнего электромагнитного поля определенной (резонансной) частоты.    3. В многоэлектронных атомах (молекулах) механические и магнитные моменты (спиновые и орбитальные) складываются так, что атом (молекула) приобретает результирующие момент импульса и магнитный дипольный момент. Правила сложения моментов обсудим только для модели так называемой рессель-саундерской связи (спин-орбитальной, LS-связи). В этой модели орбитальные моменты импульсов Ll электронов складываются в результирующий момент LL, спиновые моменты электронов Ls – в результирующий момент LS, а затем уже LL и LSобусловливают результирующий момент импульса LJ атома. Квантовое число L результирующего орбитального момента импульса LL всегда целое или нуль. Результирующее спиновое квантовое число S может быть целым или полуцелым в зависимости от того, четное или нечетное число N электронов в атоме. Если N четное, то число S принимает целочисленный ряд значений от (1/2) N до нуля (для N = 6 например, S = 3; 2; 1; 0). При нечетном N число S полуцелое от (1/2) N до 1/2 (для N = 5 ,например, S = 5/2 ; 3/2 ;1/2). При определенных числах L и S квантовое число J результирующего момента импульса атома принимает одно из следующих значений: 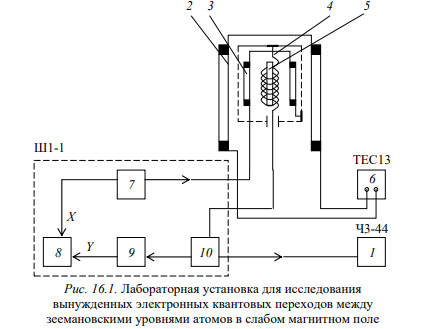  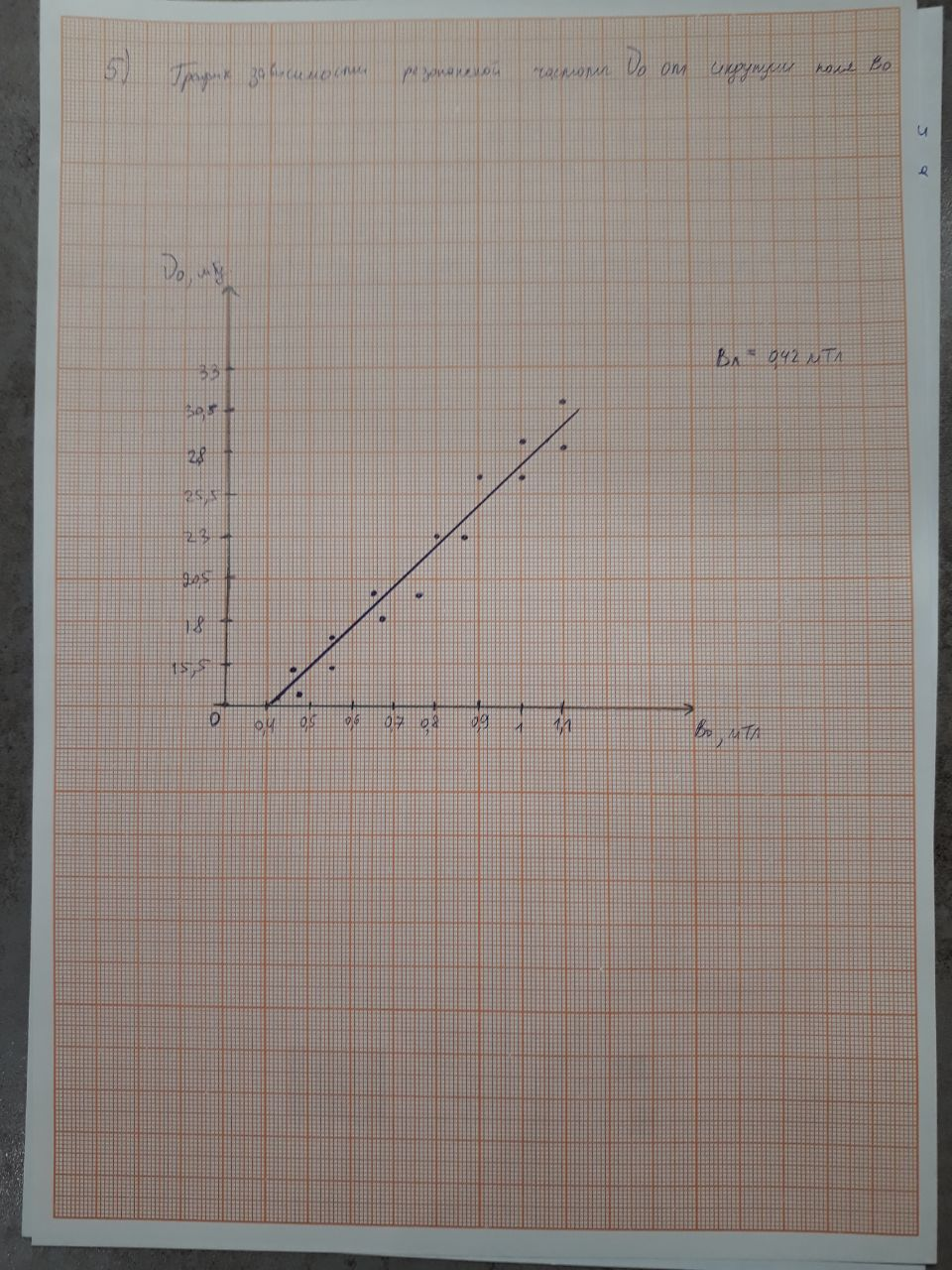  Вопросы к лабораторной работе: 1. Что составляет основу электронного парамагнитного резонанса (ЭПР)? Электронный парамагнитный резонанс (ЭПР) - явление резонансного поглощения электромагнитного излучения парамагнитным веществом, помещенным в постоянное магнитное поле. Обусловлен квантовыми переходами между магнитными подуровнями парамагнитных атомов и ионов. Метод электронного парамагнитного резонанса позволяет оценить эффекты, проявляющиеся в спектрах ЭПР из-за наличия локальных магнитных полей. В свою очередь локальные магнитные поля отражают картину магнитных взаимодействий в исследуемой системе. Таким образом, метод ЭПР спектроскопии позволяет исследовать как структуру парамагнитных частиц, так и взаимодействие парамагнитных частиц с окружением. ЭПР спектрометр предназначен для регистрации спектров и измерения параметров спектров образцов парамагнитных веществ в жидкой, твердой или порошкообразной фазе. 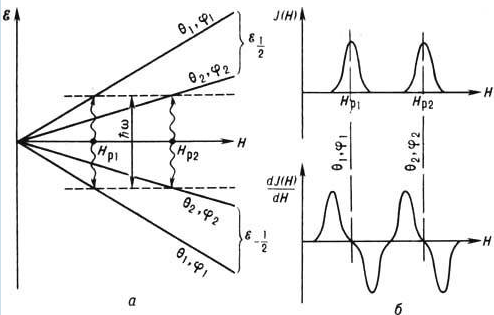 4. Назовите квантовые числа атомов. Поясните их физический смысл. n- главное квантовое число, определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы n=1,2,3,4 l=орбитальное квантовое число, определяет момент импульса электрона в атоме l=0,1,2..n-1 m - магнитное квантовое число, которое при заданном / может принимать значения т / = 0,±1,±2, ...,±1, (223.7) Квантовые числа — энергетические параметры, определяющие состояние электрона и тип орбитали, на которой он находится. 1. n - главное квантовое число определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); с 1 ( n = 1, 2, 3, .) 2. l - орбитальное (азимутальное) квантовое число определяет орбитальный момент импульса электрона. l = 0,1,...,(n -1). 3. m - магнитное квантовое число определяет проекцию момента импульса электрона на заданное направление внешнего магнитного поля. Его значения изменяются от + l до - l m= 0,±1,±2,...±l . Физический смысл магнитного квантового числа вытекает из того, что волновая функция 4. ms - спиновое квантовое число характеризует собственный момент количества движения электрона. Может принимать лишь два возможных значения±1/2 различное состояние электронов определяются непосредственно из уравнения Шредингера, кот показывает, что для каждой комбинации m,l,n будет свое распределение плотности вероятности нахождения электрона около атома. Защита: 1. Эффект Зеемана заключается в расщеплении спектральных линий атомов и ионов во внешнем магнитном поле. Расщепление спектральных линий, в свою очередь, обусловлено снятием вырождения и расщеплением энергетических состояний (появлением дополнительной энергии у магнитного момента µ, помещённого в магнитное поле с индукцией B): Eдоп = –µ•B. В зависимости от кратности вырождения состояния по квантовому числу mJ и величины индукции магнитного поля может реализовываться нормальный и аномальный эффект Зеемана, а также эффект Пашена – Бака. Объяснение эффекта Зеемана в рамках классической физики было дано Хендриком Лоренцем. Согласно его теории атом рассматривается как классический гармонический осциллятор, и его уравнение движения в присутствии магнитного поля {\displaystyle {\vec {B}},}BBBBBBBBBB направленного вдоль оси Z, можно рассматривать в виде: 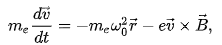 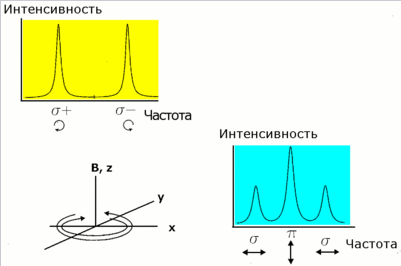  2. Квантование пространственное Квантование пространственное в квантовой механике, дискретность возможных пространственных ориентаций момента количества движения атома (или др. частицы или системы частиц) относительно любой произвольно выбранной оси (оси z). Из представлений классической физики следует, что орбитальный момент импульса электрона и пропорциональный ему магнитный момент ориентированы перпендикулярно плоскости орбиты электрона и противоположно направлены 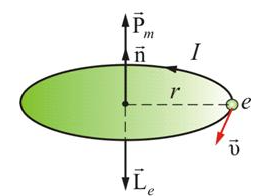 В квантовой механике, естественно, не может быть указана ориентация L и Рт относительно плоскости электронной орбиты (орбиты в буквальном смысле этого слова нет). Для указанной ориентации L и Рп должно быть выбрано некоторое направление в пространстве, и расположение L может быть задано углом между вектором L и этим направлением. За указанное направление выбирается либо направление внешнего магнитного поля, либо внутреннего, создаваемого всеми электронами, кроме рассматриваемого (но это трудно и неудобно). Как правило, берут направление внешнего магнитного поля Н, совмещенного с осью z. В классической физике представлялось само собой разумеющимся, что вектор орбитального момента импульса электрона L (или магнитного момента Рт) может быть ориентирован относительно выбранного направления произвольным образом, т. е. плоскость боровских орбит тоже может быть ориентирована произвольно. 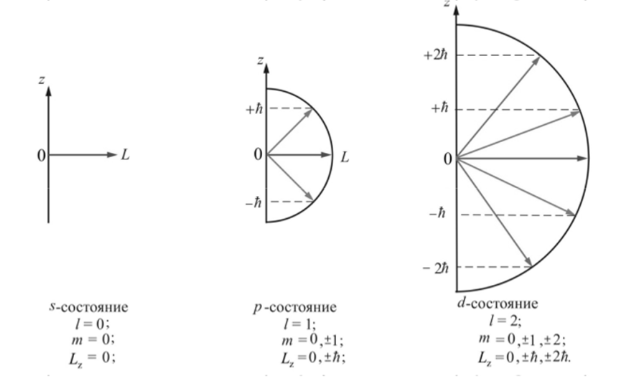 возможные ориентации вектора L в состояниях s,p4 d. 53. Вычислить кинетическую энергию W: 1) электрона; 2) молекулы кислорода (= 32 г/моль); 3) частицы, радиус которой r= 0,1 мкм и плотность = 2 г/см3, если каждой из этих частиц соответствует волна де Бройля Б = 0,1 нм  |
