Исследование функции. Исследование функции Область определения функции
 Скачать 38.66 Kb.
|
    Исследование функции 
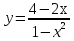
Так как функция дробно – рациональная, то в область ее определения входят те значения переменной, при которых знаменатель не обращается в нуль, то есть 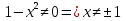 Таким образом,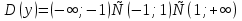 
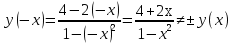 - функция не является ни четной, ни нечетной.
Найдем производную данной функции 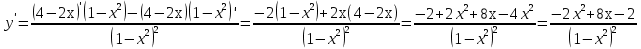 Найдем критические точки функции, то есть внутренние точки области определения функции, в которых ее производная равна нулю или не существует 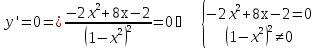 Найдем корни первого уравнения системы 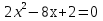 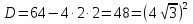 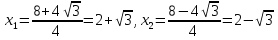 Тогда 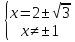 -1 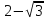 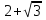 1 x - - + + - Так как на промежутках 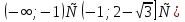 производная y’<0, то функция убывает на каждом из этих промежутков.Так как на промежутках 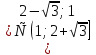 производная y’>0, то функция возрастает на каждом из этих промежутков.Так как при переходе через точку 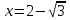 производная поменяла знак с “-” на “+”, то эта точка является точкой минимума функции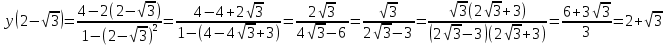 Функция имеет минимум в точке 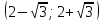 Так как при переходе через точку 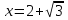 производная поменяла знак с “+” на “-”, то эта точка является точкой максимума функции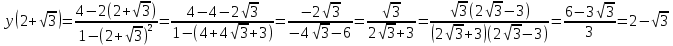 Функция имеет минимум в точке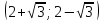 
Найдем вторую производную данной функции 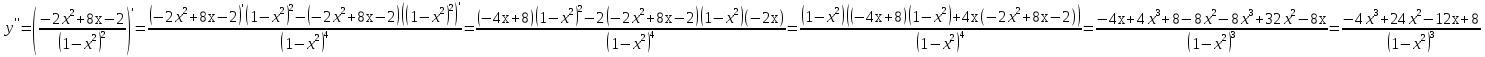 Найдем критические точки второго порядка, то есть точки, в которых производная равна нулю или не существует. Решим уравнение 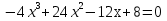 Применим подстановку 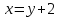 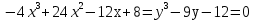 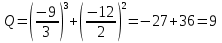 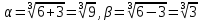 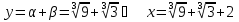 Таким образом, 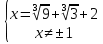 + - -1 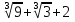 1 x - + Так как на промежутках 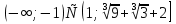 вторая производная y’’<0, то на этом промежутке график функции выпуклый.Так как на промежутках 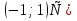 вторая производная y’’>0, то на этом промежутке график функции вогнутый.
График функции имеет две вертикальные асимптоты 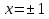 Найдем уравнение наклонной асимптоты графика заданной функции в виде 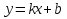 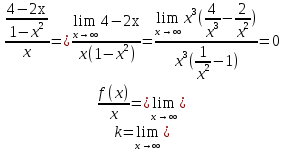 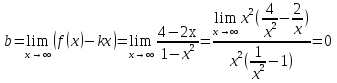 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 y -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15 -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 x 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Значит, y=0 – горизонтальная асимптота, а наклонных асимптот нет |