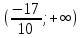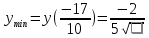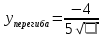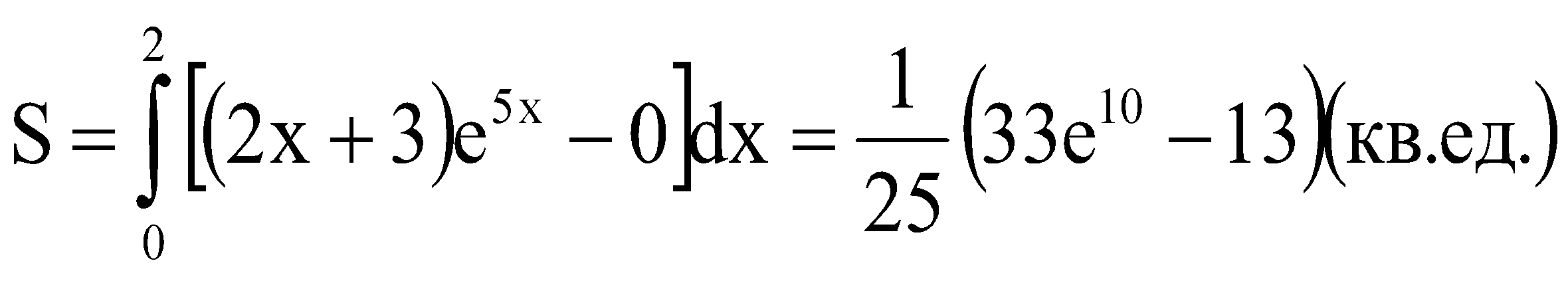Итоговое задание 1. Для функции (2 3)
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
Задание. Для функции 𝑦 = (2𝑥 + 3)𝑒5𝑥 : Найти область определения, точки разрыва. Очевидно, D(f)=(-∞;+∞) или D(f)=R. Точек разрыва нет. Исследовать функцию на четность, периодичность. Отсюда следует, что функция не является нечетной и не является четной. Функция не периодическая. Исследовать поведение функции на концах области определения. Указать асимптоты.  При х→-∞ функция стремится к нулю, При х→+∞ функция стремится +∞. Найдем наклонную асимптоту y=kx+b Следовательно, у = 0 горизонтальная асимптота при x→-∞. Так как функция не имеет точек разрыва, то это означает, что вертикальных асимптот нет. Найти промежутки монотонности. Точки экстремума. 
В окрестности точки  производная функции меняет знак с (-) на (+). Следовательно, точка производная функции меняет знак с (-) на (+). Следовательно, точка  - точка минимума. - точка минимума. Найти промежутки выпуклости. Точки перегиба.
В окрестности точки 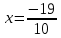 производная функции меняет знак с (-) на (+). Следовательно, точка производная функции меняет знак с (-) на (+). Следовательно, точка 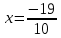 - точка перегиба. - точка перегиба. Найти площадь фигуры, ограниченной графиком функции 𝑦 = (2𝑥 + 3)𝑒5𝑥 и прямыми 𝑥 = 0, 𝑥 = 2, 𝑦 = 0. 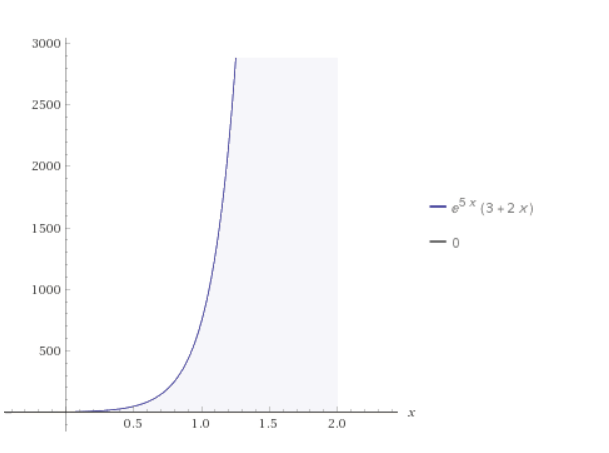 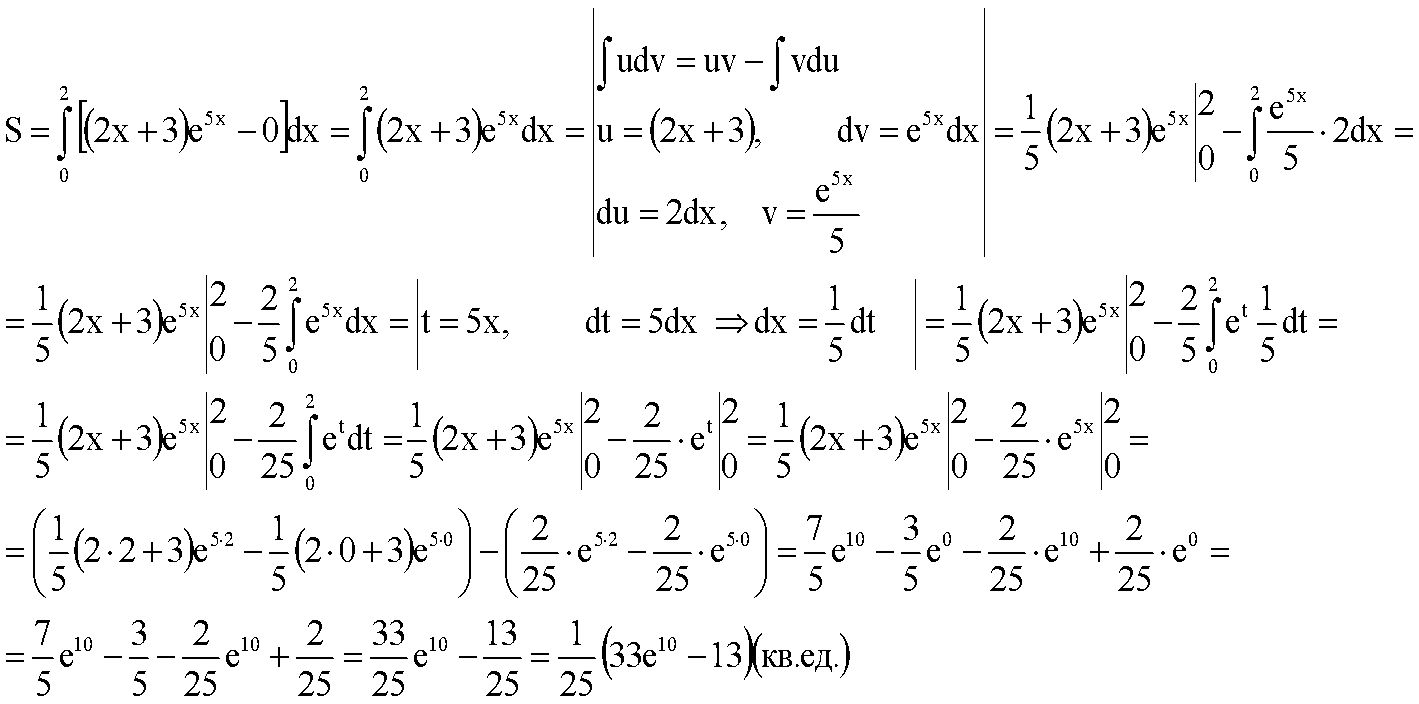 По результатам исследований построим график. 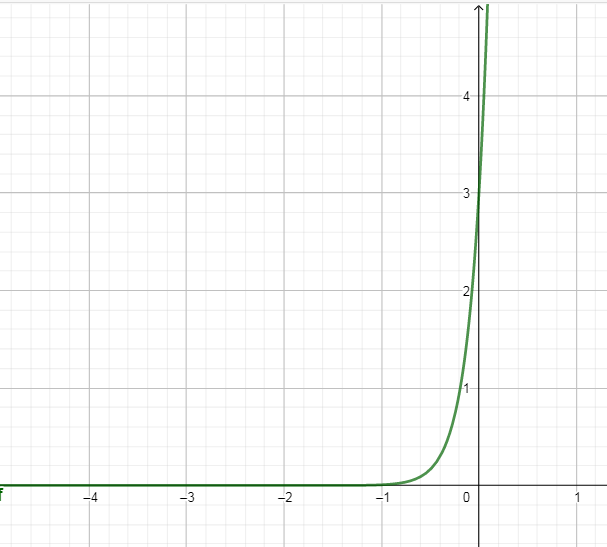 Результаты исследования оформить в виде таблицы.
|