Исследование функции. Исследование функций Шаг Общие свойства функции п. 1 Находим D
 Скачать 37.09 Kb. Скачать 37.09 Kb.
|
|
АЛГОРИТМ 8 Полное исследование функций Шаг 1. Общие свойства функции: п.1 Находим Dfи точки разрыва функции. п.2 Выясняем симметрию функции (четность, нечетность), периодичность или устанавливаем, что функция – общего вида. Шаг 2. Находим асимптоты кривой: а) вертикальные: 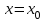 ; f(x) при ; f(x) при 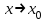 0; 0;б) наклонные: 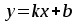 , , 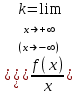 , , 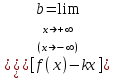 ; ;в) вертикальные (если k = 0). Шаг 3. Исследование функции на монотонность и на экстремум (с помощью 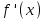 ). ).п.3 Находим 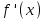 и вычисляем критические точки из уравнения и вычисляем критические точки из уравнения 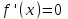 (для дифференцируемых функций) или (для дифференцируемых функций) или 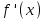 не существует. не существует.п.4 Отмечаем на числовой оси критические точки, принадлежащие Df, и определяем знаки 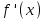 в каждом интервале. в каждом интервале.При 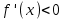 , функция , функция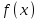 убывает, при убывает, при 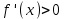 функция функция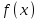 возрастает. возрастает.п.5 Определяем экстремумы функции: если при переходе через критическую точку х0 производная 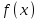 меняет знак меняет знака) с (–) на (+) – в т. х0 минимум; б) с (+) на (–) – в т. х0 максимум. Вычисляем 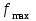 , , 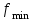 . .Шаг 4. Исследование на выпуклость, вогнутость, нахождение точек перегиба (с помощью 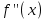 ). ).п.6 Находим 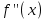 и вычисляем точки, в которых и вычисляем точки, в которых 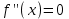 или или 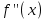 не существует. не существует.п.7 Отмечаем на числовой оси найденные точки, принадлежащие Df, и определяем знаки 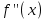 в каждом интервале: в каждом интервале: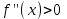 - кривая вогнута, - кривая вогнута,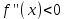 - кривая выпукла. - кривая выпукла.п.8 Если при переходе через точку х0 (где 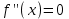 или не существует) вторая производная или не существует) вторая производная 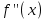 меняет знак, то х0 – точка перегиба. меняет знак, то х0 – точка перегиба.Шаг 5. Составляем таблицу из всех полученных данных исследования. Шаг 6. На основе таблицы данных изображаем график функции. При проведении частичного исследования функции выполняем следующие пункты АЛГОРИТМА: 1) исследование на монотонность – п.1, Шаг 3 п.3, 4; 2) исследование на экстремум – п.1, Шаг 3 п.3, 4, 5; 3) исследование на выпуклость, вогнутость графика функции – п.1, Шаг 4 п.6,7; 4) нахождение точек перегиба – п. 1, Шаг 4 п.6, 7, 8; 5) нахождение асимптот графика функции – Шаг 2. |
