Надежность технических систем лабораторная 1. Лабораторная работа 1. Исследование классификаций отказов по времени возникновения и последствиям

• Название: Исследование классификаций отказов по времени возникновения и последствиям
• Анкор: Надежность технических систем лабораторная 1
• Дата: 11.03.2023
• Размер: 413 Kb.
• Имя файла: Лабораторная работа 1.doc
• Тип: Исследование; #980394
• страница: 2 из 3

Показатели безотказности
Сложность и часто неопределенность процессов, происходящих в объекте и его элементах, зависимость явлений от большого числа причин (первоначального состояния, особенностей хранения, транспортировки и эксплуатации, технического обслуживания и ремонтов, квалификации обслуживающего персонала и др.) делают задачу точного определения момента отказа объекта практически неразрешимой. Поэтому его безотказность характеризуется вероятностью того или иного состояния. Основным показателем безотказности является вероятность безотказной работы p(t) – вероятность того, что в пределах заданной наработки отказ объекта не возникнет. В общем случае величина вероятности безотказной работы зависит от наработки объекта и ее конкретное значение должно быть поставлено в соответствие с определенной наработкой или временем эксплуатации объекта. Вероятность безотказной работы определяется в предположении, что в начальный момент времени (при нулевой наработке) объект работоспособен: p(0) = 1. Очевидно p(∞) = 0.

Статистическая оценка вероятности безотказной работы может быть получена в результате испытаний на надежность достаточно больших выборок. Способ вычисления зависит от плана испытаний. Для простейшего испытания N объектов до отказа последнего объекта без замен и восстановлений статистическая оценка
𝑝 ^∗ (𝑡) = 𝑁(𝑡)/𝑁(0) = 𝑁(0) – 𝑛(𝑡)/𝑁(0) = 1 – 𝑛(𝑡)/𝑁(0) (1)

где N(0) и N(t) - число работоспособных объектов при t=0 и в момент времени или при наработке t, n(t) - число отказавших объектов за время или наработку t.

В ряде случаев бывает необходимо определять вероятность безотказной работы в интервале времени (или наработки) от t₁ до t₂, представляющую собой условную вероятность того, что объект не откажет в этом интервале, при условии, что он безотказно проработал до его начала:

𝑝(𝑡₁ ,𝑡₂) = 𝑝(𝑡₂)/𝑝(𝑡₁) (2)
По аналогии с выражением статистическая оценка:
𝑝 ∗ (𝑡₁, 𝑡₂) = 𝑁(𝑡₂)/𝑁(𝑡₁) = 𝑁(0) – 𝑛(𝑡₂)/𝑁(0) – 𝑛(𝑡₁) (3)
Вероятность отказа q(t) – вероятность того, что в течение заданного времени работы или заданной наработки объект откажет хотя бы один раз. Отказ и работоспособное состояние - противоположные несовместные события, образующие полную совокупность возможных состояний объекта, поэтому в любой момент времени или при любой наработке:

𝑝(𝑡) + 𝑞(𝑡) = 1. (4)
Очевидно также, что 𝑞(0) = 0 и 𝑞(∞)= 1.

Время работы объекта до отказа в теории надежности, как правило, считается случайной величиной. Вероятность отказа совпадает с интегральной функцией распределения наработки до отказа 𝑞(t)= 𝐹(t). Статистическая оценка вероятности отказа за время или наработку t
𝑞^∗ = 𝑁(0) – 𝑁(𝑡)/𝑁(0) = 𝑛(𝑡)/𝑁(0) (5)
Вероятность безотказной работы и вероятность отказа – безразмерные величины, выражаются в долях единицы (иногда – в процентах).

Наработка до отказа - наработка объекта от начала эксплуатации до возникновения первого отказа. Наработка до отказа используется для характеристики надежности как восстанавливаемых, так и невосстанавливаемых объектов.

Средняя наработка до отказа tср – математическое ожидание наработки до отказа:
𝑡ср = 𝑀(𝑡) =∑^∞₀ [1 – 𝑞(𝑡)]𝑑𝑡 =∑^∞₀[1 – 𝐹(𝑡)]𝑑𝑡= ∑^∞₀ 𝑝(𝑡)𝑑𝑡 (6)
Статистическая оценка средней наработки до отказа
𝑡ср ^∗ = 1/𝑁(0) ∑ ^𝑁(0) _𝑖=1 t=i (7)
где ti – наработка до отказа i-го объекта.

Наработка между отказами – наработка объекта от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа. Очевидно наработка между отказами характеризует надежность только восстанавливаемых объектов.

Средняя наработка на отказ t₀- отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки, т.е. наработка, приходящая в среднем на один отказ, в рассматриваемом интервале наработки или определенной продолжительности эксплуатации:
𝑡₀ = lim_𝑛→∞ 1/𝑛∑ ⁿ _𝑖=1𝑡𝑖 (8)
где n – число отказов, ti – наработка от окончания (i–1)-го восстановления до iго отказа:
𝑡𝑖 = ∑^∞₀ [1 − 𝑞𝑖 (𝑡)] 𝑑𝑡= ∑^∞₀ [1 − 𝐹𝑖 (𝑡)]𝑑𝑡= ∑^∞₀ 𝑝𝑖 (𝑡)𝑑𝑡 (9)
где q _i (t) и p _i (t) - вероятности отказа и безотказной работы объекта от окончания (i – 1)-го восстановления до i-го отказа, F_i(t) – интегральная функция распределения вероятности наработки между (i – 1) и i-м отказами.

Статистическая оценка средней наработки на отказ
𝑡₀^∗ = 1/𝑛∑ ⁿ _𝑖=1𝑡𝑖 (10)
Гамма-процентная наработка до отказа (на отказ) tγ – наработка, в течение которой отказ объекта не возникнет с вероятностью γ (%).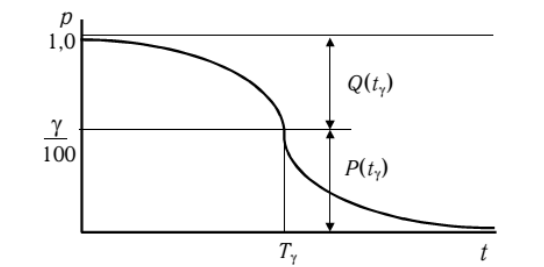



Рис. 4. Определение значения гамма-процентной наработки.
Значение гамма-процентной наработки можно определить из графика вероятности безотказной работы или уравнений (6) и (9) при p(t) = γ /100 %. При γ = 100 % гамма-процентная наработка называется установленной наработкой, при γ = 50 % – медианной.

В качестве меры продолжительности безотказной работы может быть выбран любой неубывающий параметр, характеризующий объем эксплуатации. В соответствии с этим все виды наработок могут выражаться в единицах времени или в единицах объема работы объекта (например, единицах количества продукции: для автомобилей естественной единицей измерения может служить пробег в километрах, для прокатных станов – масса прокатанного металла в тоннах и т.д.). Однако с точки зрения теории и общей методологии объективно лучшими и универсальными единицами измерения наработки являются единицы времени.

Интенсивность отказов λ(t) – условная плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник:
𝜆(𝑡)= 𝑓(𝑡)/𝑝(𝑡) (11)
где f(t) - плотность распределения наработки до отказа (частота отказов):
𝑓(𝑡) = 𝑑𝑞(𝑡)/𝑑𝑡 = − 𝑑𝑝(𝑡)/𝑑𝑡 (12)
Очевидно, что
𝜆(𝑡) = 1/1 – 𝐹(𝑡) * 𝑑𝐹(𝑡)/𝑑𝑡 = 1/1 − 𝑞(𝑡) = − 1 𝑝(𝑡) * 𝑑𝑝(𝑡)/𝑑𝑡 = − 𝑑/𝑑𝑡 [ln 𝑝(𝑡)] (13)
Тогда вероятность безотказной работы
𝑝(𝑡) = 1 – 𝑞(𝑡)= exp [-∑^t₀ 𝜆(𝑡)𝑑𝑡] (14)
Уравнение (14) – одно из основных в теории надежности. Из него следует, что вероятность безотказной работы представляет собой экспоненциальную монотонно убывающую функцию, которая в интервале времени или наработки (0,∞) изменяется от 1 до 0. Соответственно, вероятность отказа в том же интервале изменяется от 0 до 1.

Статистические оценки интенсивности отказов и плотности распределения наработки

𝜆^∗(𝑡)= 𝑛(𝑡+∆𝑡)−𝑛(𝑡)/𝑁(𝑡)∆𝑡=𝑁(𝑡)−𝑁(𝑡+∆𝑡)/𝑁(𝑡)∆𝑡 = 𝑛(𝑡,𝑡+∆𝑡)/𝑁(𝑡)∆𝑡 (15)

𝑓^∗(𝑡) = 𝑛(𝑡+∆𝑡)−𝑛(𝑡)/𝑁(0)∆𝑡=𝑁(𝑡)−𝑁(𝑡+∆𝑡)/𝑁(0)∆𝑡=𝑛(𝑡,𝑡+∆𝑡)/𝑁(0)∆𝑡 (16)

Из сравнения формул (15) и (16) следует, что интенсивность отказов и плотность распределения есть число отказов в единицу времени, отнесенное к числу работоспособных объектов (формула (15)) или к общему числу объектов (формула (16)).

Параметр потока отказов ω(t) – отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки:
𝜔(𝑡) = 𝑑𝑛(𝑡)/𝑑𝑡 (17)
где n(t) – число отказов восстанавливаемого объекта за наработку t. Статистическая оценка параметра потока отказов
𝜔∗ = 𝑛(𝑡 + 𝛥𝑡) – 𝑛(𝑡ሻ)/𝛥𝑡 (18)
В теории надежности при определении общих закономерностей для восстанавливаемых и невосстанавливаемых объектов интенсивность отказов λ(t) и параметр потока отказов ω(t) не различаются, чаще всего используется интенсивность отказов λ(t).

Из формул (11), (12) и (17) следует, что интенсивность отказов λ(t), плотность распределения наработки f(t) и параметр потока отказов ω(t) выражаются в единицах, обратных единицам наработки.

Для современных технических объектов средние наработки на отказ составляют тысячи и миллионы часов, что соответствует интенсивности отказов 10^–3-10^–6 ч ^–1 и менее. Поэтому если наработка объекта измеряется в часах, то иногда, особенно в зарубежной литературе, для упрощения записей в качестве единицы измерения интенсивности отказов используется внесистемная единица 1фит = 10^–9ч^–1. Функциональные связи между основными показателями безотказности сведены в таблицу 2.


Таблица 2

Показатели долговечности
Технический ресурс - наработка объекта от начала его эксплуатации или ее возобновления после ремонта определенного вида до перехода в предельное состояние. Технический ресурс представляет собой запас возможной наработки объекта. Для неремонтируемых объектов он совпадает с наработкой до отказа. Для ремонтируемых объектов различаются доремонтный, межремонтный, послеремонтный и полный (до списания) ресурсы.

Средний ресурс − математическое ожидание технического ресурса. Гаммапроцентный ресурс – наработка, в течение которой объект не достигает предельного состояния с вероятностью γ (%). При γ = 100 % гамма-процентный ресурс называется установленным ресурсом, при γ = 50 % – медианным.

Назначенный ресурс − суммарная наработка, при достижении которой применение объекта должно быть прекращено. Кроме того, предприятие-изготовитель или ремонтное предприятие могут установить гарантийный ресурс, в течение которого гарантируется выполнение установленных требований к объекту (при соблюдении правил его эксплуатации, хранения и транспортировки).

Все виды ресурса измеряются в единицах наработки, чаще всего − в единицах времени.

Срок службы − календарная продолжительность от начала эксплуатации объекта (или ее возобновления после ремонта определенного вида) до перехода в предельное состояние. Для ремонтируемых объектов различаются доремонтный, межремонтный, послеремонтный и полный (до списания) сроки службы.

Средний срок службы Tсл − математическое ожидание срока службы. Гамма-процентный срок службы Tγ − календарная продолжительность от начала эксплуатации объекта, в течение которой он не достигнет предельного состояния с заданной вероятностью γ (%). При γ = 100% гамма-процентный срок службы называется установленным сроком службы, при γ = 50% − медианным.

Назначенный срок службы − календарная продолжительность эксплуатации объекта, при достижении которой применение его по назначению должно быть прекращено.

Целью установления назначенного срока или назначенного ресурса является обеспечение заблаговременного прекращения применения объекта исходя из требований безопасности или по экономическим соображениям. После достижения назначенного срока службы или выработки назначенного ресурса объект может быть списан, направлен в ремонт, передан для использования не по назначению, законсервирован для хранения или может быть принято решение о продолжении эксплуатации.

Предприятие-изготовитель или ремонтное предприятие могут установить гарантийный срок службы (эксплуатации), в течение которого гарантируется выполнение установленных требований к объекту (при соблюдении правил его эксплуатации, хранения и транспортировки).

Все сроки службы измеряются в единицах календарного времени.
Показатели ремонтопригодности
Вероятность восстановления работоспособного состояния pв(t) − вероятность того, что время восстановления работоспособного состояния объекта не превысит заданного. Эта вероятность представляет собой значение интегральной функции распределения времени восстановления. Статическая оценка вероятности восстановления за время t
𝑝_в^∗(𝑡) = 𝑛(𝑡)/𝑛(0) (19)
где n(0) − число объектов при t = 0, n(t) − число восстановленных объектов за время t.
Вероятность восстановления − безразмерная величина.

Время восстановления работоспособного состояния tв − продолжительность восстановления объекта.

Среднее время восстановления − математическое ожидание времени восстановления:
𝑡_в = ∑^∞₀ [1 − 𝑝в(𝑡)]𝑑𝑡 (20)
Статистическая оценка среднего времени восстановления
𝑡_в^∗ = 1/𝑛(0) = ∑^𝑛(0)_𝑖=1 𝑡_в𝑖 (21)
Интенсивность восстановления работоспособного состояния μ(t) − условная плотность вероятности восстановления объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента восстановление не произошло:
𝜇(𝑡)= 𝑓(𝑡_в)/1 – 𝑝_в(𝑡) (22)
где 𝑓(𝑡_в) = 𝑑𝑝_в(𝑡)/𝑑𝑡 − плотность распределения времени восстановления. Тогда вероятность восстановления за время t
𝑝в(𝑡) = 1 − exp [− ∑^𝑡₀ 𝜇(𝑡)𝑑𝑡] (23)
Статистические оценки интенсивности восстановления и плотности распределения времени восстановления
𝜇^∗(𝑡)= 𝑛(𝑡)− 𝑛(𝑡 + ∆𝑡)/𝑛(𝑡)∆𝑡 , 𝑓^∗(𝑡)=𝑛(𝑡) – 𝑛(𝑡 + ∆𝑡)/𝑛(0)∆𝑡 (24)
В теории надежности часто принимается μ = const. Тогда
𝑝_в = 1– exp(– 𝜇𝑡) (25)
Время восстановления выражаются в единицах времени, интенсивность восстановления и плотность распределения − в единицах, обратных единицам времени.
Показатели сохраняемости
Срок сохраняемости – календарная продолжительность хранения и (или) транспортирования объекта, в течение и после которой сохраняются значения показателей безотказности, долговечности и ремонтопригодности в установленных пределах.

Различают срок сохраняемости до ввода в эксплуатацию и срок сохраняемости в период эксплуатации.

Средний срок сохраняемости t c - математическое ожидание срока сохраняемости.

Гамма-процентный срок сохраняемости − срок сохраняемости, достигаемый объектом с заданной вероятностью γ (%). При γ = 100% гамма-процентный срок сохраняемости называется установленным сроком сохраняемости, при γ = 50% − медианным.

Сроки сохраняемости измеряются в единицах календарного времени.
Комплексные показатели надежности
При оценке эксплуатационной надежности технических систем широко используются комплексные показатели, характеризующие одновременно несколько свойств надежности (безотказность, ремонтопригодность, долговечность). Наиболее распространенными комплексными показателями являются коэффициенты готовности, оперативной готовности и технического использования.

Коэффициент готовности Kг − вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Коэффициент готовности характеризует готовность объекта к применению только в отношении его работоспособности и, следовательно, означает вероятность застать объект в работоспособном состоянии в произвольный момент времени, причем этот момент не может быть выбран в тех интервалах времени, где применение объекта исключено. Коэффициент определяется как отношение математического ожидания времени нахождения объекта в работоспособном состоянии к сумме математических ожиданий этого времени и времени внеплановых ремонтов:
𝐾г = 𝑡/𝑡 + 𝑡_в (26)
где t - средняя наработка на отказ, tв − среднее время восстановления.

Коэффициент оперативной готовности Kог − вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени. Коэффициент характеризует надежность объектов, необходимость применения которых возникает в произвольный момент времени, после которого требуется определенная безотказная работа. До этого момента объекты могут находиться в режиме дежурства или выполнять другие функции, возможно возникновение отказов и восстановление работоспособности. Коэффициент оперативной готовности
𝐾_ог = 𝐾_г × 𝑝(𝑡₀,t) (27)
Здесь t0 − момент, когда возникает необходимость применения объекта; t − момент, когда его применение прекращается.

Коэффициент технического использования Kти − отношение математического ожидания интервалов времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к сумме математических ожиданий интервалов времени пребывания объекта в работоспособном состоянии, простоев, обусловленных техническим обслуживанием, и ремонтов за тот же период эксплуатации:
𝐾_ти = 𝑡/𝑡 + 𝑡_в+𝑡_то (28)
Коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии в течение рассматриваемого периода эксплуатации, включая периоды всех видов технического обслуживания и ремонтов.

Коэффициент планируемого применения Kп − доля периода эксплуатации, в течение которого объект не должен находиться на плановом техническом обслуживании и ремонте. Коэффициент планируемого применения − отношение заданной продолжительности плановых технических обслуживаний и ремонтов за этот период к его продолжительности.