Исследование контактных явлений в структуре металлполупроводник
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра МИТ ОТЧЕТ По индивидуальному домашнему заданию По дисциплине «Основы электротехники и радиоматериалов» Тема: Исследование контактных явлений в структуре металл-полупроводник. Студентка гр.0183 __________________ Ершова С.А. Преподаватель __________________ Мельник В.И. Санкт-Петербург 2022 Задание для варианта №8: 13,5,5 Таблица 1. Некоторые свойства металлов 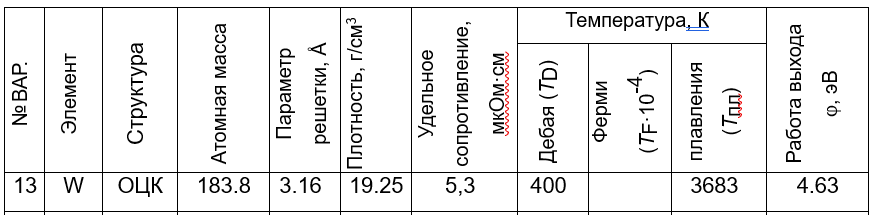 Таблица 2. Свойства собственных полупроводников 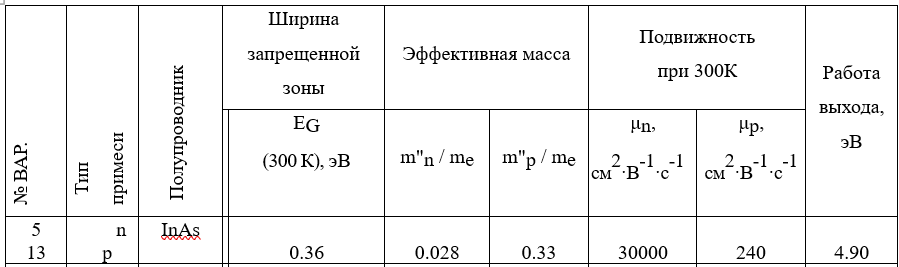 Таблица 3. Концентрация n- и p- примесей в полупроводниках  Формулировка задания: Для заданной пары металл-полупроводник оценить кинетические свойства заданных материалов, рассчитать и построить энергетическую диаграмму и вольтамперную характеристику контакта в заданном диапазоне температур, дать рекомендации по применению исследуемого контакта. Задание 1: Определить класс симметрии заданных материалов, построить прямую и обратную элементарные ячейки заданных материалов. Определить размеры Зоны Бриллюэна в направлениях X, L, К. Кристалл вольфрама имеет объемноцентрированную кубическую решетку. В объемно-центрированной кубической ячейке вольфрама атомы располагаются по вершинам и в центре ячейки, т.е. на одну ячейку приходится два атома. 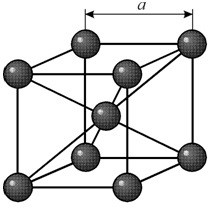 Рис. 1. Вид ОЦК-решетки Определим класс симметрии: 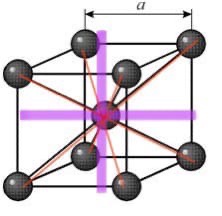 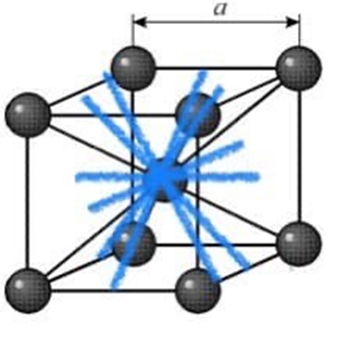 Где красные линии- Поворотные оси симметрии L3 Фиолетовые- Поворотные оси симметрии L4. Синие линии- поворотные оси симметрии L2, пересекаются в центре симметрии С. Рис.2, 3. Оси симметрии 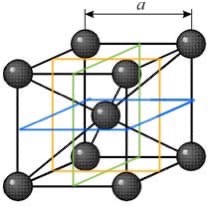 Где желтая, синяя, зеленая плоскости- плоскости симметрии. 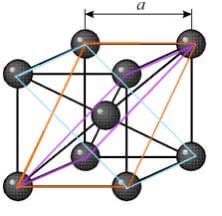 Где голубая, оранжевая и фиолетовая плоскости- плоскости симметрии. Г 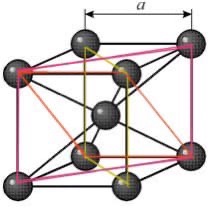 де розовая, оранжевая и оливковая плоскости- плоскости симметрии. де розовая, оранжевая и оливковая плоскости- плоскости симметрии.Рис. 4,5,6- плоскости симметрии. Объемноцентрированная кубическая решетка имеет три координатных плоскости и шесть диагональных плоскостей. Формула симметрии куба: 3L4 4L3 6L2 9P C. Класс симметрии: m3m. Построим обратную элементарную решетку. Определим базисные вектора для данной структуры решетки. 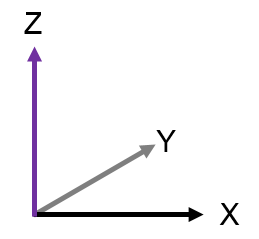                     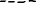     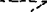 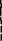      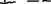   Рис. 7. Базисные вектора в прямом пространстве. Направляющие (базисные) вектора прямой решетки: 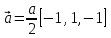 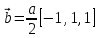 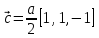 Объем решетки: 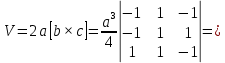 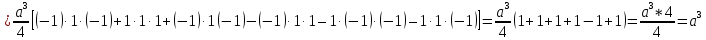 При a=3,16* 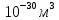 : :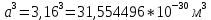 Направляющие (базисные) вектора обратной решетки: 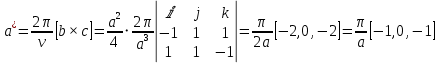 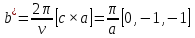 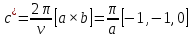 Построим на векторах 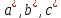 обратную решетку: обратную решетку: 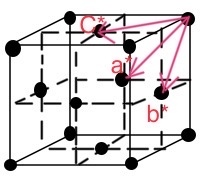 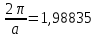 Рис.8. Базисные вектора в обратном пространстве. 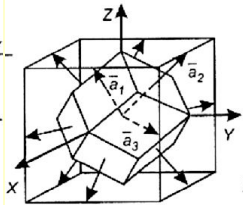 Рис. 9. Вид ячейки Вигнера-Зейтса для ГЦК-решетки. 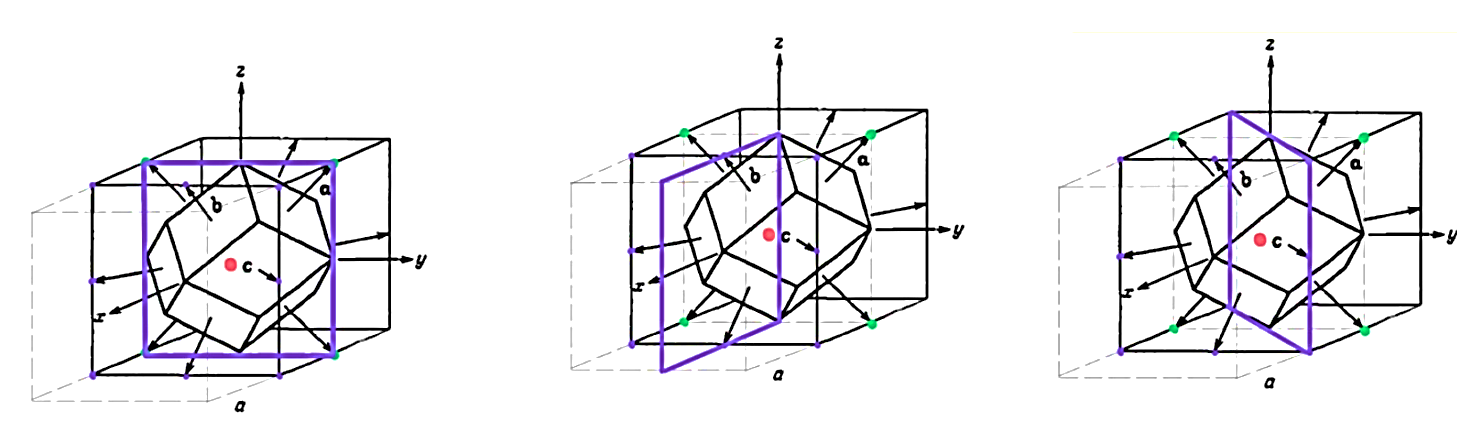 Рис. 10. Вспомогательные плоскости для нахождения ОХ, ОL и ОК ячейки Вигнера-Зейтса. 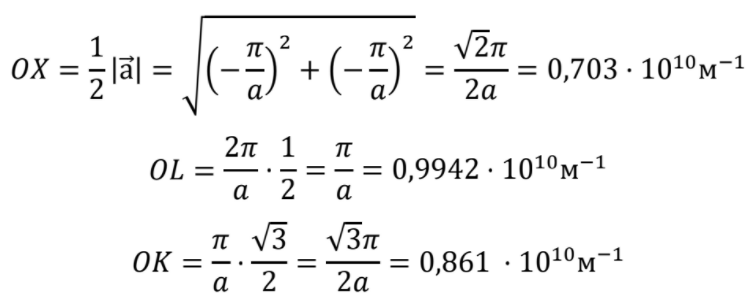 |
