тоэ. Исследование линейной цепи несинусоидального тока
 Скачать 111.91 Kb. Скачать 111.91 Kb.
|
 РОСЖЕЛДОР РОСЖЕЛДОРДВГУПС Кафедра «ЭтЭЭм» ЛАБОРАТОРНАЯ РАБОТА на тему: «Исследование линейной цепи несинусоидального тока» ЛР 23.05.05 221 005 Выполнил: Паршин В.А. Проверил: Гафиатулина Е.С. Хабаровск-2021 Цель работы: Исследование линейной цепи несинусоидального тока и влияния характера цепи на форму кривых тока и напряжения; получение навыков расчета цепей несинусоидального тока. Основные положения: Несинусоидальное напряжение можно представить в виде ряда Фурье 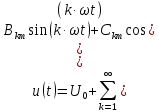 Где 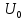 - постоянная составляющая; - постоянная составляющая; 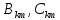 – амплитуды синусоидальных и косинусоидальных составляющих, соответственно. Величины – амплитуды синусоидальных и косинусоидальных составляющих, соответственно. Величины 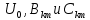 определяется по известным из математики формулам. определяется по известным из математики формулам. При электрических расчетов ряд Фурье удобнее представить в виде 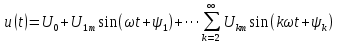 Где 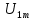 – амплитуда первой (основной) гармонической составляющей (гармоники); – амплитуда первой (основной) гармонической составляющей (гармоники); 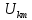 – амплитуды высших гармоник; – амплитуды высших гармоник; 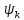 – начальная фаза к-той гармоники – начальная фаза к-той гармоникиВеличины амплитуд и начальных фаз гармоник можно определить по формулам 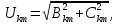 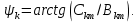 Если несинусоидальное напряжение приложено к линейной цепи, то при расчете применяется метод наложения, и каждая гармоника рассчитывается отдельно. При этом, естественно, ограничиваются каким-то предельным числом гармоник, которое зависит от вида решаемой задачи и требуемой точности расчета. Рассчитывая постоянную составляющую, следует помнить, что для постоянного тока емкость представляет разрыв цепи, а индуктивность имеет нулевое сопротивление. Расчет синусоидальных составляющих удобно проводить в символическом виде. Ток каждой гармоники на входе цепи при известном напряжении можно определить по закону Ома 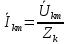 где 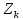 – комплексное входное сопротивление цепи для к-той гармоники. Величина – комплексное входное сопротивление цепи для к-той гармоники. Величина 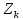 Рассчитывается точно также как для обычной цепи синусоидального тока, но определение индуктивных и емкостных сопротивлений необходимо вести с учетом угловой частоты каждой гармоники Рассчитывается точно также как для обычной цепи синусоидального тока, но определение индуктивных и емкостных сопротивлений необходимо вести с учетом угловой частоты каждой гармоники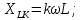 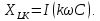 Мгновенное значение тока на входе цепи также представляется в виде ряда Фурье и записывается как сумма рассчитанных постоянной составляющей и мгновенных значений всех гармоник. Действующее значение несинусоидальной величины можно определить по формулам 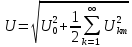 ; ;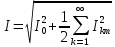 . .Активная мощность равна 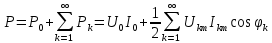 , ,где 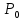 – мощность постоянной составляющей; – мощность постоянной составляющей; 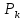 – активная мощность к-той гармоники; – активная мощность к-той гармоники; 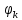 – угол сдвига фаз между током и напряжением к-той гармоники: – угол сдвига фаз между током и напряжением к-той гармоники: 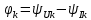 . .   3’ м 2’3 м 2 м Ход работы:                                      v VV V м 1 м R м W A м Генератор     1’       Для заданного преподавателем варианта срисовать схему, снять показания приборов и зарисовать кривые напряжений в точках 1-1’, 2-2’ и 3-3’. Показания приборов занести в таблицу:
Имея кривую мгновенного значения напряжения на входе (точки 1-1’), разложить его в ряд Фурье, ограничившись постоянной составляющей и тремя гармониками. Рассчитать мгновенные значения тока в цепи и напряжений на активном сопротивлении и реактивном элементе. Записать выражение тока в виде ряда Фурье. Рассчитать действующее значение напряжения и тока на входе цепи, а также величину активной мощности цепи. Построить составляющие ряда Фурье входного напряжения и суммарную кривую. Для сравнения на этом же рисунке привести кривую, снятую в входе эксперимента. 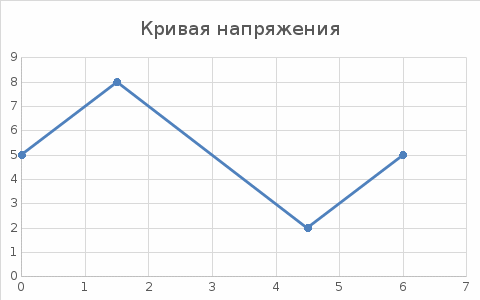 Рисунок 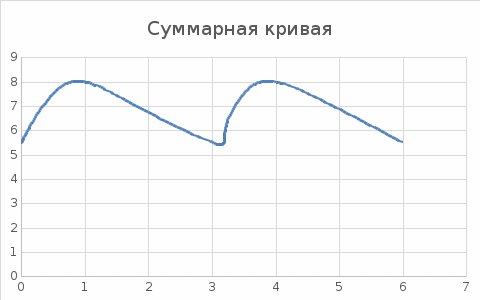 Рисунок  Рисунок |
